Tổng các số tự nhiên m để hàm số y=x4-2(m-1)x2+m-2 đồng biến trên khoảng
(1;3) là
A. 1 B. 0 C. 2 D. 3
Những câu hỏi liên quan
Có bao nhiêu số thực m để hàm số
y
1
5
m
2
x
5
-
1
4
(
m
+
2
)
x
4
+
1
3
x
3
+
1
2
(
m
2...
Đọc tiếp
Có bao nhiêu số thực m để hàm số y = 1 5 m 2 x 5 - 1 4 ( m + 2 ) x 4 + 1 3 x 3 + 1 2 ( m 2 - 1 ) x 2 + 1 đồng biến trên khoảng - ∞ ; + ∞
A. 2
B. 1
C. Vô số
D. 0
Có 
.
Nhận thấy g(0)=0 do đó trước tiên cần có 
+) Với 
(thỏa mãn);
+) Với 
(loại).
Vậy m = -1 là giá trị cần tìm duy nhất.
Chọn đáp án B.
Đúng 0
Bình luận (0)
Tìm tất cả các giá trị thực của tham số m sao cho hàm số
y
x
4
-
2
(
m
-
1
)
x
2
+
m
-
2
đồng biến trên khoảng (1;3). A. . B. . C....
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m sao cho hàm số y = x 4 - 2 ( m - 1 ) x 2 + m - 2 đồng biến trên khoảng (1;3).
A. 
.
B. 
.
C. 
.
D. 
.
.
với 
, 
, 
.
.Tìm tất cả các giá trị thực của tham số m sao cho hàm số
y
x
4
-
2
(
m
-
1
)
x
2
+
m
-
2
đồng biến trên khoảng (1;3)? A.
m
∈
[
-
5
;
2
)
B. m
∈
(-
∞
;2] C....
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m sao cho hàm số y = x 4 - 2 ( m - 1 ) x 2 + m - 2 đồng biến trên khoảng (1;3)?
A. m ∈ [ - 5 ; 2 )
B. m ∈ (- ∞ ;2]
C. m ∈ ( 2 ; + ∞ )
D. m ∈ ( - ∞ ; - 5 )
Tìm tất cả các giá trị thực của tham số m sao co hàm số y = x4 - 2(m - 1)x2 + m - 2 đồng biến trên khoảng (1;3)?
Tất cả các giá trị của tham số m để hàm số
y
x
4
-
2
(
m
-
1
)
x
2
+
m
-
2
đồng biến trên (1;5) là A. m2 B. 1 m 2 C. m ≤ 2 D. 1 ≤ m ≤ 2
Đọc tiếp
Tất cả các giá trị của tham số m để hàm số y = x 4 - 2 ( m - 1 ) x 2 + m - 2 đồng biến trên (1;5) là
A. m<2
B. 1 < m < 2
C. m ≤ 2
D. 1 ≤ m ≤ 2
Gọi T là tập hợp tất cả các giá trị nguyên dương của tham số m để hàm số
y
x
4
-
2
m
x
2
+
1
đồng biến trên khoảng
2
;
+
∞
. Tổng giá trị các phần tử của T là A. 8 B. 10 C. 4 D. 6
Đọc tiếp
Gọi T là tập hợp tất cả các giá trị nguyên dương của tham số m để hàm số y = x 4 - 2 m x 2 + 1 đồng biến trên khoảng 2 ; + ∞ . Tổng giá trị các phần tử của T là
A. 8
B. 10
C. 4
D. 6
Cho hàm số
y
x
4
-
2
m
x
2
-
3
m
+
1
(
1
)
(m là tham số). Tìm m để hàm số (1) đồng biến trên khoảng (1;2). A.. B.. C.. D..
Đọc tiếp
Cho hàm số y = x 4 - 2 m x 2 - 3 m + 1 ( 1 ) (m là tham số). Tìm m để hàm số (1) đồng biến trên khoảng (1;2).
A.
.
B.
.
C.
.
D.
.
ChọnA
Ta có 
.
+ 
, 
⇒
thoả mãn.
+ 
, 
có 3 nghiệm phân biệt: 
..
Hàm số (1) đồng biến trên (1; 2)
. Vậy 
.
Đúng 0
Bình luận (0)
Tìm tất cả các giá trị thực của tham số m sao cho hàm số
y
x
4
-
2
n
-
1
x
2
+
m
-
2
đồng biến trên khoảng (1; 3)? A.
m
∈
[
-
5
;
2
)
B.
m
∈
(
-
∞
;
2...
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m sao cho hàm số y = x 4 - 2 n - 1 x 2 + m - 2 đồng biến trên khoảng (1; 3)?
A. m ∈ [ - 5 ; 2 )
B. m ∈ ( - ∞ ; 2 ]
C. m ∈ 2 ; + ∞
D. m ∈ - ∞ ; - 5
Chọn B.
Tập xác định D = R.
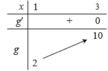
Dựa vào bảng biến thiên, kết luận: m ≤ min g(x) ⇔ m ≤ 2
Đúng 0
Bình luận (0)
Tìm tất cả các giá trị thực của tham số m để hàm số
y
x
4
−
2
x
2
+
2
m
2
−
1
x
+
5
đồng biến trên khoảng
1
;
+
∞
.
A. ...
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để hàm số y = x 4 − 2 x 2 + 2 m 2 − 1 x + 5 đồng biến trên khoảng 1 ; + ∞ .
A. − 2 2 ≤ m ≤ 2 2
B. − 2 2 < m < 2 2
C. m < − 2 2 hoặc m > 2 2
D. m ≤ − 2 2 hoặc m ≥ 2 2
Đáp án D
Hàm số đồng biến trên khoảng:
1 ; + ∞ ⇔ y ' ≥ 0 , ∀ x ∈ 1 ; + ∞ .
Ta có: y ' = 4 x 3 − 4 x + 2 m 2 − 1 ⇒ y ' ≥ 0
⇔ f x = 4 x 3 − 4 x − 1 ≥ − 2 m 2 , x ∈ 1 ; + ∞ ⇒ − 2 m 2 ≤ min 1 ; + ∞ f x .
Ta có: f ' x = 12 x 2 − 4 ⇒ f ' x = 0 ⇔ x = ± 1 3 .
Có bảng biến thiên hàm số f(x) như sau:
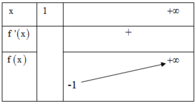
Từ bảng biến thiên , suy ra f x > − 1 , x ∈ 1 ; + ∞
⇒ − 2 m 2 ≤ − 1 ⇔ m 2 ≥ 1 2 ⇔ m ≥ 2 2 m ≤ − 2 2
Đúng 0
Bình luận (0)
Có bao nhiêu số nguyên dương m để hàm số y = x 4 - m x 2 đồng biến trên khoảng (1;+∞).
A. 1.
B. 4.
C. 2.
D. 3.
