Tìm X
23x+2 bằng 4x+5
Tính các giới hạn lim x → + ∞ x 3 3 x 2 - 4 - x 2 3 x + 2
Cộng hai phân thức x 2 3 x + 3 + 2 x + 1 3 x + 3
Hướng dẫn:
Ta có:
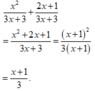
+ Cộng hai phân thức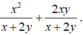
Ta có: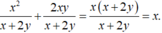
tìm giá trị lớn nhất
A bằng -x^2 cộng 4x cộng 7
B bằng -4x^2 cộng 4x - 5
C bằng -x^2 cộng x cộng 5
\(A=-x^2+4x+7=-\left(x^2-4x+4\right)+11=-\left(x-2\right)^2+11\)
Ta thấy : \(-\left(x-2\right)^2+11\le11\)\(\Leftrightarrow maxA=11\)khi \(x=2\)
\(B=-4x^2+4x-5=-\left(4x^2-4x+1\right)-4=-\left(2x-1\right)^2-4\)
Ta thấy : \(-\left(2x-1\right)^2-4\le-4\)\(\Leftrightarrow maxB=-4\)khi \(x=\frac{1}{2}\)
\(C=-x^2+x+5=-\left(x^2-2\cdot\frac{1}{2}\cdot x+\frac{1}{4}\right)+\frac{21}{4}=-\left(x-\frac{1}{2}\right)^2+\frac{21}{4}\)
Ta thấy : \(-\left(x-\frac{1}{2}\right)^2+\frac{21}{4}\le\frac{21}{4}\)\(\Leftrightarrow maxC=\frac{21}{4}\)khi \(x=\frac{1}{2}\)
tk mk nka !!!
Cho y=2x+7,y=4x-5
Tìm tọa độ giao điểm của 2 đồ thị bằng phép tính
Gọi \(A\left(x;y\right)\) là tọa độ giao điểm của 2 đồ thị.
2 đồ thị \(y=2x+7;y=4x-5\) giao nhau khi :
\(2x+7=4x-5\\ \Leftrightarrow2x-4x=-5-7\\ \Leftrightarrow-2x=-12\\ \Leftrightarrow x=6\)
Thay \(x=6\) vào \(y=2x+7\Rightarrow y=2.6+7=19\)
Vậy \(A\left(6;19\right)\)
bài 1
tìm gtng và gtln
d=-4x^2 -4x +3
c= 9x^2 +6x +2
e=25x^2 +16x +4
bài 2 cho đa thức x^4 - x^3 +6x^2 -x +a chia cho x^2 -x +5 tìm a để số dư bằng 0
bài 1
tìm gtng và gtln
d=-4x^2 -4x +3
c= 9x^2 +6x +2
e=25x^2 +16x +4
bài 2 cho đa thức x^4 - x^3 +6x^2 -x +a chia cho x^2 -x +5 tìm a để số dư bằng 0
botay.com.vn
a) x4+x3+2x2+x+1=(x4+x3+x2)+(x2+x+1)=x2(x2+x+1)+(x2+x+1)=(x2+x+1)(x2+1)
b)a3+b3+c3-3abc=a3+3ab(a+b)+b3+c3 -(3ab(a+b)+3abc)=(a+b)3+c3-3ab(a+b+c)
=(a+b+c)((a+b)2-(a+b)c+c2)-3ab(a+b+c)=(a+b+c)(a2+2ab+b2-ac-ab+c2-3ab)=(a+b+c)(a2+b2+c2-ab-ac-bc)
c)Đặt x-y=a;y-z=b;z-x=c
a+b+c=x-y-z+z-x=o
đưa về như bài b
d)nhóm 2 hạng tử đầu lại và 2hangj tử sau lại để 2 hạng tử sau ở trong ngoặc sau đó áp dụng hằng đẳng thức dề tính sau đó dặt nhân tử chung
e)x2(y-z)+y2(z-x)+z2(x-y)=x2(y-z)-y2((y-z)+(x-y))+z2(x-y)
=x2(y-z)-y2(y-z)-y2(x-y)+z2(x-y)=(y-z)(x2-y2)-(x-y)(y2-z2)=(y-z)(x2-2y2+xy+xz+yz)
Tìm x,biết:
a) 3x2 - 10x + 7 bé hơn hoặc bằng 0
b) 4x2 + 9x + 5 lớn hơn hoặc bằng 0
a) \(3x^2-10x+7\)
\(=3\left(x^2-\frac{10}{3}x+\frac{7}{3}\right)\)
\(=3\left(x^2-\frac{10}{3}x+\frac{25}{9}-\frac{4}{9}\right)\)
\(=3\left[\left(x-\frac{5}{3}\right)^2-\frac{4}{9}\right]\)
\(=3\left[\left(x-\frac{5}{3}\right)^2\right]-\frac{4}{3}\ge\frac{-4}{3}>0\)
b) \(4x^2+9x+5\)
\(=4x^2+9x+\frac{81}{16}-\frac{1}{16}\)
\(=\left(2x+\frac{9}{4}\right)^2-\frac{1}{16}\ge\frac{-1}{16}>0\)
cho hàm số y= f(x)=4x-12
a tính f(-2); f(3)
b tìm x khi y bằng 5
a, Ta có : f[32]=2⋅32=3f[32]=2⋅32=3
f[−12]=2⋅[−12]=−1f[−12]=2⋅[−12]=−1
b, f(x)=−4f(x)=−4
⇔2x=−4⇔2x=−4
⇔x=(−4):2=−2
liếm loz,liếm loz
Tìm x lớp 8
2(4x-5)^2-4x+5= 0
Tìm x lớp 8
2(4x-5)^2-4x+5= 0
\(2\left(4x-5\right)^2-4x+5=0\)
\(\Leftrightarrow2\left(4x-5\right)^2-\left(4x-5\right)=0\)
\(\Leftrightarrow\left(4x-5\right)\left(8x-10-1\right)=0\)
\(\Leftrightarrow\left(4x-5\right)\left(8x-11\right)=0\)
\(\Leftrightarrow\hept{\begin{cases}4x-5=0\\8x-11=0\end{cases}\Leftrightarrow\hept{\begin{cases}x=\frac{5}{4}\\x=\frac{11}{8}\end{cases}}}\)
2(4x-5)^2 -4x+5 =0
(8x-10)(4x-5)-(4x-5) =0
(8x-11)(4x-5)=0
Suy ra: (8x-11)(4x-5) =0
Do đó: 8x-11=0 hoặc 4x-5=0
x=11/8 hoặc x=5/4
Vậy x=11/8 hoặc x=5/4
\(2\left(4x-5\right)^2-4x+5=0\)
\(\Leftrightarrow\)\(\left(4x-5\right)\left[2\left(4x-5\right)-1\right]=0\)
\(\Leftrightarrow\)\(\left(4x-5\right)\left(8x-11\right)=0\)
\(\Leftrightarrow\)\(\orbr{\begin{cases}4x-5=0\\8x-11=0\end{cases}}\)
\(\Leftrightarrow\)\(\orbr{\begin{cases}x=\frac{5}{4}\\x=\frac{11}{8}\end{cases}}\)
Vậy...
Tìm x biết:
(4x - 3)( 4x + 2) + (4x + 5)(1 - 4x) =2.52
(4x-3).(4x+2) + (4x+5).(1-4x) = 2.52
16x2 + 8x - 12x - 6 + 4x - 16x2 + 5 - 20x = 50
(16x2 - 16x2) + ( 8x-12x+4x-20x) - (6-5) = 50
-20x = 50
x = -5/2