Cho tam giác đều ABC , E là điểm trên cạnh AC ( E khác A ) ; F là hình chiếu vuông góc của E trên AB. Đường thẳng qua C vuông góc với BC cắt đường thẳng È ở D. Gọi K là trung điểm của AE, H là điểm đối xúng với D qua K

Những câu hỏi liên quan
Cho tam giác ABC đều cố định gọi M là trung điểm của BC hai điểm E và F theo thứ tự lần lượt di chuyển trên cạnh AB và cạnh AC sao cho góc EMF= 60 độ (E khác A và B,F khác A và C) xác định vị trí điểm e trên cạnh AB sao cho AE+AF lớn nhất
Cho tam giác ABC cân tại A Trên cạnh AB lấy điểm E (E khác A và B) trên cạnh AC lấy điểm F (E khác A và C) sao cho AE= AF Gọi M là trung điểm của EF Trên tia đối của tia MB lấy điểm D sao cho MD = MB Chứng minh tam giác BME bằng tam giác DMF
a, tu ve hinh :
tamgiac ABC can tai A => AB = AC va goc ABC = goc ACB (gn)
goc AIC = goc AIB = 90 do AI | BC (gt)
=> tamgiac AIC = tamgiac AIB (ch - gn)
=> IB = IC (dn)
b, dung PY-TA-GO
c, AE = AF (gt) => tamgiac AFE can tai E (dn)
=> goc AFE = (180 - goc BAC) : 2 (tc)
tamgiac ABC can tai A (gt) => goc ACB = (180 - goc BAC) : 2 (tc)
=> goc AFE = goc ACB ma 2 goc nay dong vi
=> EF // BC (dh)
vay_
Cho tam giác ABC đều có cạnh 1 trên cạnh AC lấy các điểm D và E sao cho góc ABD góc CBE 20 độ.Gọi M là trung điểm BE, N là điểm trên cạnh BC sao cho BN BM.Tính tổng diện tích 2 tam giác Cho tam giác ABC đều có cạnh 1 trên cạnh AC lấy các điểm D và E sao cho góc ABD góc CBE 20 độ.Gọi M là trung điểm BE, N là điểm trên cạnh BC sao cho BN BM.Tính tổng diện tích 2 tam giác DCE và tam giác BCE và tam giác BENgiúp với
Đọc tiếp
Cho tam giác ABC đều có cạnh = 1 trên cạnh AC lấy các điểm D và E sao cho góc ABD = góc CBE = 20 độ.Gọi M là trung điểm BE, N là điểm trên cạnh BC sao cho BN = BM.Tính tổng diện tích 2 tam giác Cho tam giác ABC đều có cạnh = 1 trên cạnh AC lấy các điểm D và E sao cho góc ABD = góc CBE = 20 độ.Gọi M là trung điểm BE, N là điểm trên cạnh BC sao cho BN = BM.Tính tổng diện tích 2 tam giác DCE và tam giác BCE và tam giác BEN
giúp với
Cho tam giác ABC vuông tại A có góc C 30 độ . trên cạnh AB lấy M sao cho góc BCM 2/3 góc ACB, trên cạnh AC lấy điểm N sao cho góc CBN bằng 2/3 góc ABC . gọi giao điểm của CM và BN là K .a ) Tính góc CKNb ) Gọi F và I theo thứ là hình chiếu của điểm K trên BC và AC. Trên tia đối của tia IK lấy điểm D sao cho IK ID, trên tia KF lấy điểm E sao cho KF FE ( E khác K ) . Chứng minh tam giác DBC là tam giác đều
Đọc tiếp
Cho tam giác ABC vuông tại A có góc C = 30 độ . trên cạnh AB lấy M sao cho góc BCM = 2/3 góc ACB, trên cạnh AC lấy điểm N sao cho góc CBN bằng 2/3 góc ABC . gọi giao điểm của CM và BN là K .
a ) Tính góc CKN
b ) Gọi F và I theo thứ là hình chiếu của điểm K trên BC và AC. Trên tia đối của tia IK lấy điểm D sao cho IK = ID, trên tia KF lấy điểm E sao cho KF = FE ( E khác K ) . Chứng minh tam giác DBC là tam giác đều
Cho tam giác ABC có góc A là góc tù. Trên cạnh AB lấy điểm D (khác A và B), trên cạnh AC lấy điểm E (khác A và C). CMR DE<BC
1,Cho tam giác ABC. Trên cạnh AC lấy điểm E cố định , trên cạnh BC lấy điểm F cố định ( E khác A và C; F khác B và C). Trên cạnh AB lấy điểm D di động ( D khác A và B) . Hãy xác định vị trí điểm D trên đường thẳng AB sao cho DE^2+DF^2 có giá trị nhỏ nhất. 2,Cho tam giác ABC vuông tại A có đường cao AH. Gọi I là tâm đg tròn nội tiếp tam giác, E,F,D lần lượt là hình chiếu của I trên AC, AB,BC.Gọi M là trung điểm AC.MI cắt AB tại N.FD cắt AH tại P. Chứng minh ANAP
Đọc tiếp
1,Cho tam giác ABC. Trên cạnh AC lấy điểm E cố định , trên cạnh BC lấy điểm F cố định ( E khác A và C; F khác B và C). Trên cạnh AB lấy điểm D di động ( D khác A và B) . Hãy xác định vị trí điểm D trên đường thẳng AB sao cho DE^2+DF^2 có giá trị nhỏ nhất.
2,Cho tam giác ABC vuông tại A có đường cao AH. Gọi I là tâm đg tròn nội tiếp tam giác, E,F,D lần lượt là hình chiếu của I trên AC, AB,BC.Gọi M là trung điểm AC.MI cắt AB tại N.FD cắt AH tại P. Chứng minh AN=AP
Cho tam giác ABC vuông ở A, điểm I trên cạnh AC. Vẽ đường tròn đường kính IC cắt BC ở E, cắt BI ở D (D khác I). Chứng minh:
a)4 điểm A, B, C, D cùng nằm trên một đường tròn; 4 điểm A, B, E, I cùng nằm trên một đường tròn.
b) I cách đều 3 cạnh của tam giác ADE
c) 3 đường thẳng AB, CD, EI đồng qui
Mn ơi giúp e với =')
Giữ lời hứa 1 câu trl 3 coin
Tổng cộng mốt e đủ coin thì e đưa cj 6 coin , h cj cho khất nợ:)
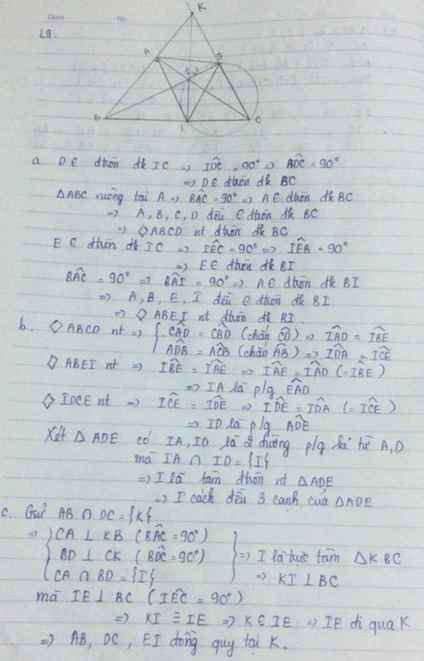
Đúng 1
Bình luận (2)
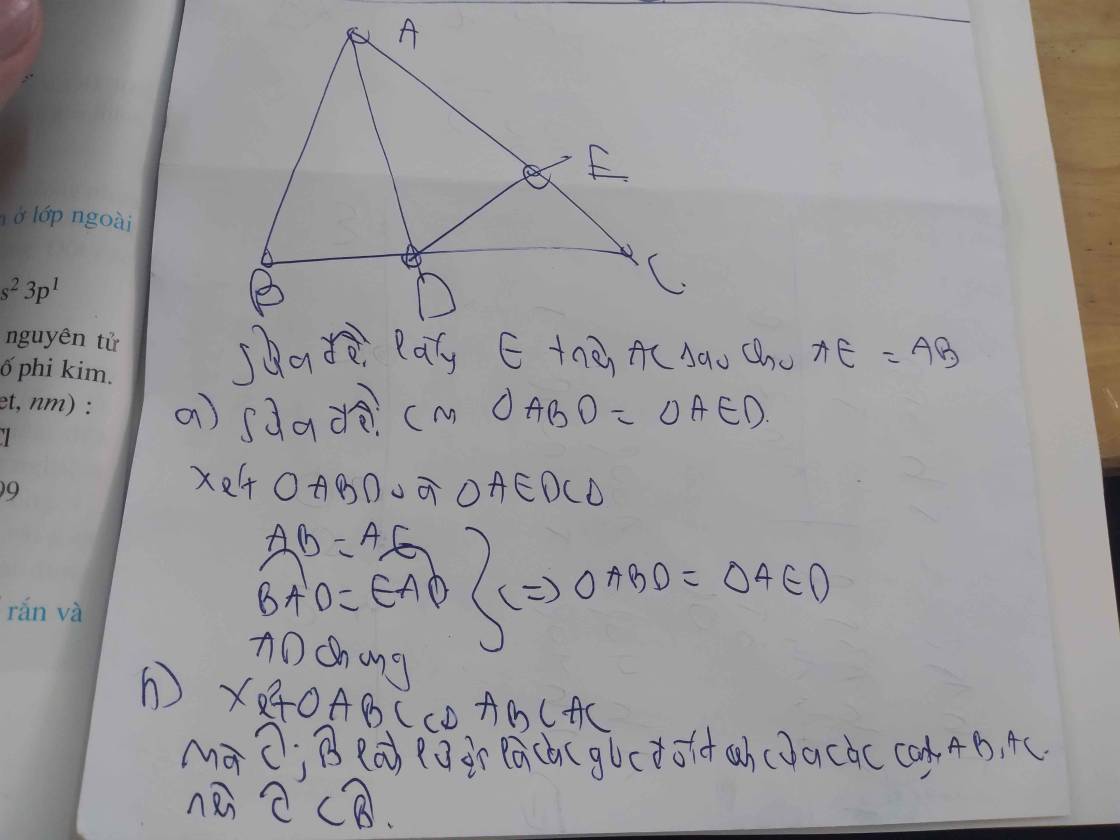
Cho ABC có ( AB < AC) và AD là phân giác của A (DE BC). Gọi E là một điểm bất kỳ thuộc cạnh AD(E khác A;D). Trên cạnh AC lấy điểm F sao cho AF = AB . a) Chứng minh: tam giác ABE = tam giác AFE.
b) So sánh các góc B.và C. So sánh AD và AC biết ADC = 105°
cho tam giác ABC nhọn, AB<AC .Trên cạnh AB lấy điểm D(D khác A và B),trên cạnh AC lấy điểm E sao cho góc ADE = ACB
a) CM : tam giác ADE đồng dạng tam giác ACB
b)Gọi i là giao điểm của BC và DE. CM: IB.IC=ID.IE
c)Lấy M là trung điểm BC . CM \(\dfrac{AD.AB}{AE.AM}\) =2
a: Xet ΔADE và ΔACB có
góc ADE=góc ACB
góc DAE chung
=>ΔADE đồng dạng với ΔACB
b: Xét ΔIDB và ΔICE có
góc IDB=góc ICE
góc I chung
=>ΔIDB đồng dạng với ΔICE
=>ID/IC=IB/IE
=>ID*IE=IB*IC
Đúng 0
Bình luận (0)