Cho hàm số f(x) thõa mãn
2f(x)-x×f(-x)=x +10.tính f(2)
Những câu hỏi liên quan
Cho hàm số f(x) thỏa mãn
∫
0
1
(
x
+
1
)
f
(
x
)
d
x
10
và 2f(1) – f(0) 2. Tính I
∫
0
1
f
(
x
)
d
x
A. I -12. B. I 8. C. I 12. D. I -8.
Đọc tiếp
Cho hàm số f(x) thỏa mãn ∫ 0 1 ( x + 1 ) f ' ( x ) d x = 10 và 2f(1) – f(0) = 2. Tính I = ∫ 0 1 f ( x ) d x
A. I = -12.
B. I = 8.
C. I = 12.
D. I = -8.
Chọn D.
Đặt u = x + 1 d v = f ' ( x ) d x ⇒ d u = d x v = ∫ f ' ( x ) d x
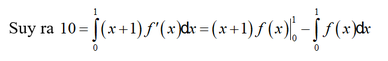
⇔ 10 = 2f(1) – f(0) – I ⇔ 10 = 2 – I ⇔ I = -8.
Đúng 0
Bình luận (0)
Cho hàm số f(x) thỏa mãn
∫
0
1
(
x
+
1
)
f
(
x
)
d
x
10
và 2f(1) - f(0) 2 .Tính tích phân
I
∫
0
1
f
(
x
)
d
x
.
A. I-12. B. I8. C. I12. D. I-8
Đọc tiếp
Cho hàm số f(x) thỏa mãn ∫ 0 1 ( x + 1 ) f ' ( x ) d x = 10 và 2f(1) - f(0) = 2 .Tính tích phân I = ∫ 0 1 f ( x ) d x .
A. I=-12.
B. I=8.
C. I=12.
D. I=-8
cho hàm số f(x) xác định với mọi x thỏa mãn f(X) +2f(1/x) = X^2 tính f(1/3)
hàm số f(x) xác định với mọi x thỏa mãn \(f\left(x\right)+2f\left(\frac{1}{x}\right)=x^2\)nên:
+) x = 3 thì \(f\left(3\right)+2f\left(\frac{1}{3}\right)=\frac{1}{9}\Rightarrow2f\left(3\right)+4f\left(\frac{1}{3}\right)=\frac{2}{9}\)(1)
+) x = \(\frac{1}{3}\)thì \(f\left(\frac{1}{3}\right)+2f\left(3\right)=9\)(2)
Lấy (1) - (2) ta được: \(3f\left(\frac{1}{3}\right)=\frac{-79}{9}\)
\(\Rightarrow f\left(\frac{1}{3}\right)=\frac{-79}{27}\)
Làm ngược, sửa:))
+) Nếu x = 3 thì \(f\left(3\right)+2f\left(\frac{1}{3}\right)=9\Rightarrow2f\left(3\right)+4f\left(\frac{1}{3}\right)=18\)(1)
+) Nếu x = \(\frac{1}{3}\) thì \(f\left(\frac{1}{3}\right)+2f\left(3\right)=\frac{1}{9}\)(2)
Lấy (1) - (2) ta được: \(3f\left(\frac{1}{3}\right)=\frac{161}{9}\)
\(\Rightarrow f\left(\frac{1}{3}\right)=\frac{161}{7}\)
Cho hàm số f (x) nhận giá trị dương và có đạo hàm liên tục trên đoạn [0;3] thoả mãn f(0)2,f(3)8 và
∫
0
3
(
f
(
x
)
)
2
f
(
x
)
d
x...
Đọc tiếp
Cho hàm số f (x) nhận giá trị dương và có đạo hàm liên tục trên đoạn [0;3] thoả mãn f(0)=2,f(3)=8 và ∫ 0 3 ( f ' ( x ) ) 2 f ( x ) d x = 8 3 . Tính f(2).
A. 50/9.
B. 49/9.
C. 47/9.
D. 52/9
Cho f(x) và g(x) là hai hàm số liên tục trên đoạn [1;3], thỏa mãn:
∫
1
3
[
f
(
x
)
+
3
g
(
x
)
]
d
x
10
và
∫
1
3
[
2
f
(
x
)
-
g
(
x
)
]
d
x...
Đọc tiếp
Cho f(x) và g(x) là hai hàm số liên tục trên đoạn [1;3], thỏa mãn: ∫ 1 3 [ f ( x ) + 3 g ( x ) ] d x = 10 và ∫ 1 3 [ 2 f ( x ) - g ( x ) ] d x = 6 . Tính I = ∫ 1 3 [ f ( x ) + g ( x ) ] d x
A. I=8
B. I=9
C. I=6
D. I=7
Cho hàm số f (x) nhận giá trị dương và có đạo hàm liên tục trên đoạn [0;2] thoả mãn f(0)3,f(2)12 và
∫
0
2
(
f
(
x
)
)
2
f
(
x
)
d
x
6...
Đọc tiếp
Cho hàm số f (x) nhận giá trị dương và có đạo hàm liên tục trên đoạn [0;2] thoả mãn f(0)=3,f(2)=12 và ∫ 0 2 ( f ' ( x ) ) 2 f ( x ) d x = 6 . Tính f(1).
A. 27 4
B. 25 4
C. 9 2
D. 15 4
Cho hàm số f(x) nhận giá trị dương và có đạo hàm liên tục trên đoạn [0;2] thoả mãn f(0) 3; f(2) 12 và
∫
0
2
(
f
(
x
)
)
2
f
(
x
)
d
x...
Đọc tiếp
Cho hàm số f(x) nhận giá trị dương và có đạo hàm liên tục trên đoạn [0;2] thoả mãn f(0) = 3; f(2) = 12 và ∫ 0 2 ( f ' ( x ) ) 2 f ( x ) d x = 6 Tính f(1)
A. 27/4
B. 25/4
C. 9/2
D. 15/4
Theo bất đẳng thức Cauchy-Schwarz cho tích phân có:
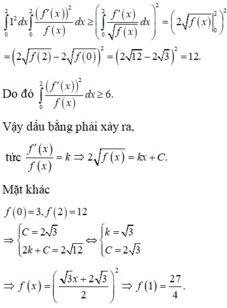
Đáp án A
Đúng 0
Bình luận (0)
Cho hàm số y f(x) xác định trên R, thỏa mãn f(x)0 và f(x) + 2f(x) 0. Tính f(-1), biết rằng f(1) 1 A.
e
-
2
B.
e
3
C.
e
4
D. e
Đọc tiếp
Cho hàm số y = f(x) xác định trên R, thỏa mãn f(x)>0 và f'(x) + 2f(x) = 0. Tính f(-1), biết rằng f(1) = 1
A. e - 2
B. e 3
C. e 4
D. e
Cho hàm số f(x) thỏa mãn f(x) + 2f(2 - x) = 3x với mọi số thực x. Vậy f(2) =
Cho hàm số f(x) thỏa mãn f(x) + 2f(2 - x) = 3x với mọi số thực x. Vậy f(2) =