Cho tam giác ABC cân tại A, đường trung tuyến CM và đường trung tuyến CD cắt nhau tại A
a, Tính chu vi và diện tích của tứ giác BMDC, BC = 8cm, AB = 5cm.
b, Qua điểm H kẻ đường thẳng song song với AB cắt AB, ÁC tại Q và K

Những câu hỏi liên quan
cho tam giác abc cân tại a có ab<bc, các đường trung tuyến be và cf cắt nhau tại h.
a)biết bc = ? cm . tính ef
b)từ e kẻ de song song vs ab. tính db và dc
c)gọi i và k lần lượt là trung điểm của ec và fb . tính ik
d) biết ad=12cm . tính p (chu vi )của hình thang bcef
a: Xét ΔABC có
F là trung điểm của AB
E là trung điểm của AC
Do đó: FE là đường trung bình của ΔBAC
Suy ra: \(FE=\dfrac{BC}{2}\) và FE//BC
b: Xét tứ giác FEDB có
FE//BD
FB//DE
Do đó: FEDB là hình bình hành
Suy ra: FE=BD
mà \(FE=\dfrac{BC}{2}\)
nên \(BD=\dfrac{BC}{2}\)
\(\Leftrightarrow BD=CD=\dfrac{BC}{2}\)
c: Hình thang FECB có
K là trung điểm của FB
I là trung điểm của EC
Do đó: KI là đường trung bình của hình thang FECB
Suy ra: KI//FE//BC và \(KI=\dfrac{1}{2}\left(FE+BC\right)\)
\(\Leftrightarrow KI=\dfrac{1}{2}\left(\dfrac{1}{2}BC+BC\right)\)
\(\Leftrightarrow KI=\dfrac{1}{2}\left(\dfrac{3}{2}BC\right)\)
\(\Leftrightarrow KI=\dfrac{3}{4}BC\)
Đúng 1
Bình luận (0)
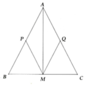
Cho tam giác ABC cân tại A, trung tuyến AM. Qua M kẻ đường thẳng song song với AC cắt AB tại P và đường thẳng song song với AB cắt AC tại Q.
a) Tứ giác APMQ là hình gì? Vì sao?
b) Chứng minh PQ//BC
a) Vận dụng đinh lý 1 về đường trung bình của tam giác suy ra APMQ là hình thoi do có 4 cạnh bằng nhau.
b) Vì PQ ^ AM mà AM ^ BC (tính chất tamgiacs cân) nên PQ//BC.
Đúng 0
Bình luận (0)
Cho tam giác ABC có đường trung tuyến AM và trọng tâm G. Qua G kẻ đường thẳng song song với AB cắt BC tại H. Từ H kẻ đường thẳng song song song với AC cắt AB ở K. a) Tính tỉ số b) Tứ giác BKGH là hình gì? Vì sao? c) Tìm điều kiện của tam giác ABC để tứ giác BKGH là hình thoi? hình vuông?
Tam giác ABC cân tại A , trung tuyến AM . Qua M kẻ đường thẳng song song với AC cắt AB tại P và đường thẳng song song với AB cắt AC tại Q.
a) Tứ giác APMQ là hình gì? Tại sao?
b) Chứng minh PQ// BC
c) Gọi D là điểm đối xứng với M quaQ. Chứng minh tứ giácADMB là hình bình hành;
d) Tìm điều kiện của tam giác ABC để tứ giác ADCM là hình vuông?
a: ΔABC cân tại A
mà AM là đường trung tuyến
nên AM là đường cao và AM là phân giác của \(\widehat{BAC}\)
Xét tứ giác APMQ có
AP//MQ
AQ//MP
Do đó: APMQ là hình bình hành
Hình bình hành APMQ có AM là phân giác của góc PAQ
nên APMQ là hình thoi
b: Xét ΔABC có
M là trung điểm của BC
MP//AC
Do đó: P là trung điểm của AB
Xét ΔABC có
M là trung điểm của BC
MQ//AB
Do đó: Q là trung điểm của AC
Xét ΔABC có
P,Q lần lượt là trung điểm của AB,AC
=>PQ là đường trung bình của ΔABC
=>PQ//BC
c: Xét ΔABC có M,Q lần lượt là trung điểm của CB,CA
=>MQ là đường trung bình của ΔABC
=>MQ//AB và \(MQ=\dfrac{AB}{2}\)
mà \(MQ=\dfrac{MD}{2}\)
nên MD=AB
MQ//AB
=>MD//AB
Xét tứ giác ABMD có
AB//MD
AB=MD
Do đó: ABMD là hình bình hành
d: Xét tứ giác AMCD có
Q là trung điểm chung của AC và MD
Do đó: AMCD là hình bình hành
Hình bình hành AMCD có \(\widehat{AMC}=90^0\)
nên AMCD là hình chữ nhật
Hình chữ nhật AMCD muốn trở thành hình vuông thì CA là phân giác của góc MCD
=>\(\widehat{ACB}=\dfrac{1}{2}\cdot90^0=45^0\)
Đúng 1
Bình luận (1)
Cho tam giác ABC cân tại A có trung tuyến AM qua B kẻ đường thẳng song song với AC cắt đường thẳng AB tại D
a chứng minh tam giác ABC bằng tam giác DMB
b Chứng minh AB = BD
C Gọi I là trung điểm của AB đoạn thẳng PD cắt đường thẳng bc tại O Trên tia đối của tia PO lấy điểm N sao cho BN = PO .Chứng minh O là trọng tamm của tam giác ABB và NA=20M
Cho tam giác ABC cân tại A, có góc A nhọn. Vẽ AH vuông góc với BC tại H.
a) CM: tam giác ABH = tam giác ACH.
b) Vẽ đường trung tuyến BK của tam giác ABC cắt AH tại O. Qua H kẻ đường thẳng song song với AC, đường thẳng này cắt AB tại I. CM: tam giác HAI cân và ba điểm C, O, I thẳng hàng.
c) CM: AH > CH.
mk ko bt lm câu c nha ~~ xl ~~~~
https://h.vn/hoi-dap/tim-kiem?q=Cho+tam+gi%C3%A1c+ABC+c%C3%A2n+t%E1%BA%A1i+A.+K%E1%BA%BB+AH+vu%C3%B4ng+g%C3%B3c+BC+t%E1%BA%A1i+H++a)+CM+tam+gi%C3%A1c+ABH=tam+gi%C3%A1c+ACH++b)+V%E1%BA%BD+trung+tuy%E1%BA%BFn+BM.+G%E1%BB%8Di+G+l%C3%A0+giao+%C4%91i%E1%BB%83m+c%E1%BB%A7a+AH+v%C3%A0+BM.+Ch%E1%BB%A9ng+minh+G+l%C3%A0+tr%E1%BB%8Dng+t%C3%A2m+c%E1%BB%A7a+tam+gi%C3%A1c+ABC++c)+Cho+AB=30cm,+BH=18cm.+T%C3%ADnh+AH,AG++d)+T%E1%BB%AB+H+k%E1%BA%BB+HD+song+song+v%E1%BB%9Bi+AC(D+thu%E1%BB%91c+AB),+ch%E1%BB%A9ng+minh+ba+%C4%91i%E1%BB%83m+C,G,D+th%E1%BA%B3ng+h%C3%A0ng&id=248109
Cho tam giác ABC vuông tại A. AB 7,5 cm; BC 12,5 cm. a) Tính diện tích tam giác ABC. b) Lấy điểm M trên cạnh AB sao cho AM : MB 1 : 2. Từ M kẻ đường thẳng song song với BC cắt trung tuyến AF tại E và cắt cạnh AC tại N. Chứng minh E là trung điểm của MN. c) Gọi G, H lần lượt là trung điểm của MC, BN. Chứng minh EGFH là hình chữ nhật và tính diện tích của nó.
Đọc tiếp
Cho tam giác ABC vuông tại A. AB = 7,5 cm; BC = 12,5 cm.
a) Tính diện tích tam giác ABC.
b) Lấy điểm M trên cạnh AB sao cho AM : MB = 1 : 2. Từ M kẻ đường thẳng song song với BC cắt trung tuyến AF tại E và cắt cạnh AC tại N. Chứng minh E là trung điểm của MN.
c) Gọi G, H lần lượt là trung điểm của MC, BN. Chứng minh EGFH là hình chữ nhật và tính diện tích của nó.
a) Học sinh tự làm
b) Chứng minh A N 1 2 N C ⇒ S A M E = S A E N ⇒ E M = E N
hay E là trung điểm MN.
c) Chứng minh được EG//HF và HE/FG nên EHFG là hình bình hành; Mặt khác BM ^ NC (do AB ^ AC)
Suy ra EHFG là hình chữ nhật

Đúng 0
Bình luận (0)
Cho ABC cân tại A, có BAC nhọn. Vẽ AH vuông góc BC tại H. a) Chứng minh: ABH ACH. b) Vẽ đường trung tuyến BK của tam giác ABC cắt AH tại O. Qua H kẻ đường thẳng song song với AC, đường thẳng này cắt AB tại I. Chứng minh: ΔHAI cân và 3 điểm C, O, I thẳng hàng. c) Chứng minh: AH CH
Cho tam giác ABC vuông tại A. AB 7,5 cm; BC 12,5cm. a) Tính diện tích tam giác ABC. b) Lấy điểm M trên cạnh AB sao cho AM: MB 1:2. Từ M kẻ đường thẳng song song với BC cắt trung tuyến AF tại E và cắt cạnh AC tại N. Chứng minh E là trung điểm của MN. c) Gọi G, H, I thứ tự là trung điểm của MC, NB và FE. Chứng minh G, H, I thẳng hàng và tính diện tích ∆IHF
Đọc tiếp
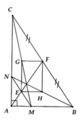
Cho tam giác ABC vuông tại A. AB = 7,5 cm; BC = 12,5cm.
a) Tính diện tích tam giác ABC.
b) Lấy điểm M trên cạnh AB sao cho AM: MB = 1:2. Từ M kẻ đường thẳng song song với BC cắt trung tuyến AF tại E và cắt cạnh AC tại N. Chứng minh E là trung điểm của MN.
c) Gọi G, H, I thứ tự là trung điểm của MC, NB và FE. Chứng minh G, H, I thẳng hàng và tính diện tích ∆IHF
a) AC = 10cm Þ SABC =37,5 (cm2)
b) Chứng minh được M A E ^ = A M E ^ (cùng = A B C ^ ) Þ AE = ME. Cmtt ta có AE = NE. Từ đó suy ra ME = NE.
c) Chứng minh EH//GF (//MB) và GE//FH (//NC) Þ EGFH là hình bình hành. Chứng minh được H E G ^ = B A C ^ = 90 0 ⇒ E G F H là hình chữ nhật. Suy ra GH đi qua trung điểm của EF.
S E G F H = H E . E G = 1 2 M B . 1 2 N C = 1 4 . 2 3 A B . 2 3 A C = 25 3 ( c m 2 )
Mà S E G F H = 4. S ⇒ I H F S I H F = 25 12 c m 2
Đúng 0
Bình luận (0)













