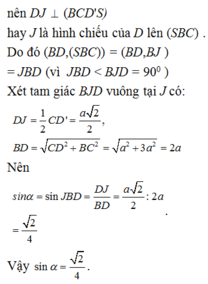Cho hình bình hành ABCD có góc A =α và BD ⊥ BC , AB= a. Tính diện tích ABCD theo a và α

Những câu hỏi liên quan
Cho hình bình hành ABCD có BD vuông góc với BC. Biết AB=a, góc A = α . Tính diện tích hình bình hành ABCD theo a và α
Cho hình bình hành ABCD có góc A =α và BD ⊥ BC , AB= a. Tính diện tích ABCD theo a và α
Hình bình hành ABCD . BD vuông góc với Bc. AB=a, góc A là góc anpha. Tính diện tích hình bình hành ABCD theo a và anpha
Cho hình thang ABCD có AB//CD có góc nhọn BCD = α ; BC = m ; CD = n
a) Tính diện tích , chu vi và các đường chéo của hình thang ABCD theo m ; n và góc alpha
b) Tính diện tích , chu vi và các đường chéo của hình thang ABCD biết m = 4,25 cm ; n = 7,56 cm ; α=54∘30′
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật,
A
B
a
,
B
C
a
3
,
S
A
a
và SA vuông góc với đáy ABCD. Tính
sin
α
, với
α
là góc tạo bởi giữa đường thẳng BD và mặt phẳng
S
B
C
. A.
sin...
Đọc tiếp
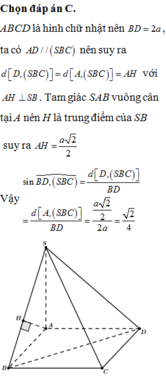
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, A B = a , B C = a 3 , S A = a và SA vuông góc với đáy ABCD. Tính sin α , với α là góc tạo bởi giữa đường thẳng BD và mặt phẳng S B C .
A. sin α = 7 8
B. sin α = 3 2
C. sin α = 2 4
D. sin α = 3 5
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB a , BC
a
3
, SA a và SA vuông góc với đáy ABCD. Tính sin
α
với
α
là góc tạo bởi giữa đường thẳng BD và mặt phẳng
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB = a , BC = a 3 , SA = a và SA vuông góc với đáy ABCD. Tính sin α với α là góc tạo bởi giữa đường thẳng BD và mặt phẳng
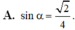
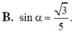
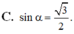
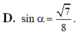
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật,
A
B
a
,
B
C
a
3
,
S
A
a
và SA vuông góc với đáy ABCD. Tính sin
α
với
α
là góc tạo bởi đường thẳng BD và mặt phẳng (SBC)
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, A B = a , B C = a 3 , S A = a và SA vuông góc với đáy ABCD. Tính sin α với α là góc tạo bởi đường thẳng BD và mặt phẳng (SBC)


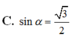

#SGD Bắc Giang – năm 2017 – 2018~Cho hình chóp S. ABCD có đáy ABCD là hình chữ nhật, ABa, BC a
3
, SAa và SA vuông góc với đáy ABCD. Tính sin α, với α là góc tạo bởi giữa đường thẳng BD và mặt phẳng (SBC).
Đọc tiếp
#SGD Bắc Giang – năm 2017 – 2018~Cho hình chóp S. ABCD có đáy ABCD là hình chữ nhật, AB=a, BC = a 3 , SA=a và SA vuông góc với đáy ABCD. Tính sin α, với α là góc tạo bởi giữa đường thẳng BD và mặt phẳng (SBC).
![]()
![]()
![]()
![]()
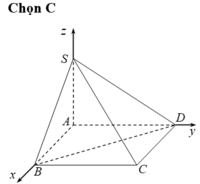
Đặt hệ trục tọa độ Oxyz như hình vẽ.
Khi đó, ta có A (0;0;0), B (a;0;0), D (0; a√3 ; 0), S (0;0;a).
Ta có ![]() , nên đường thẳng BD có vectơ chỉ phương là
, nên đường thẳng BD có vectơ chỉ phương là ![]() .
.
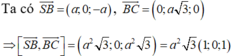
Như vậy, mặt phẳng (SBC) có vectơ pháp tuyến là ![]()
Do đó, α là góc tạo bởi giữa đường thẳng BD và mặt phẳng (SBC) thì
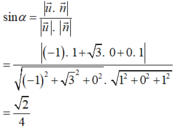
Đúng 0
Bình luận (0)
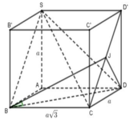
Cho hình chóp S. ABCD có đáy là hình bình hành tâm O có AC a và BD b. Tam giác SBD là tam giác đều. Một mặt phẳng (α) di động song song với mặt phẳng (SBD) và đi qua điểm I trên đoạn OA và AI x ( 0 x a) . Xác định thiết diện của hình chóp cắt bởi mặt phẳng (α) và tính dienj tích thiết diện theo a; b và x? A.
b
2
x
2
2
a...
Đọc tiếp
Cho hình chóp S. ABCD có đáy là hình bình hành tâm O có AC= a và BD= b. Tam giác SBD là tam giác đều. Một mặt phẳng (α) di động song song với mặt phẳng (SBD) và đi qua điểm I trên đoạn OA và AI = x ( 0< x< a) . Xác định thiết diện của hình chóp cắt bởi mặt phẳng (α) và tính dienj tích thiết diện theo a; b và x?
A. b 2 x 2 2 a 2
B. b 2 x 2 3 2 a 2
C. b 2 x 2 3 a 2
D. Đáp án khác
Cho hình chóp S. ABCD có đáy là ABCD là hình chữ nhật có AB a, BC 2a. Hai mp (SAB)và mp (SAD) cùng vuông góc với mặt phẳng đáy, cạnh SC hợp với mặt đáy một góc
α
. Tính thể tích khối chóp S. ABCD theo
α
A.
2
a
3
15
3
B.
2
a
3...
Đọc tiếp
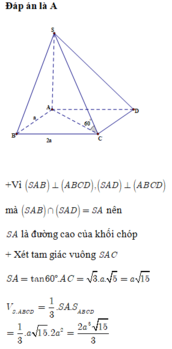
Cho hình chóp S. ABCD có đáy là ABCD là hình chữ nhật có AB = a, BC= 2a. Hai mp (SAB)và mp (SAD) cùng vuông góc với mặt phẳng đáy, cạnh SC hợp với mặt đáy một góc α . Tính thể tích khối chóp S. ABCD theo α
A. 2 a 3 15 3
B. 2 a 3 15
C. 2 a 3
D. 2 a 3 15 9