Mn giải giúp mình bài 2 mình cần gấp .

Những câu hỏi liên quan
Mn giúp mình giải bài này với mình đang cần gấp
\(\Rightarrow U=IR=24.0,5=12V\)
vay phai dat vao 2 dau bong den 1 HDT=12V
Đúng 3
Bình luận (0)
Mn giúp mình giải bài này với mình đang cần gấp
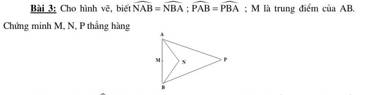
Mn giải giúp mình bài này nha! Mình đang cần gấp.
Xét tam giác NAB cân tại N, có M là trung điểm của AB suy ra NM vuông góc với AB (1)
Xét tam giác APB cân tại P, có M là trung điểm của AB suy ra MP vuông góc với AB (2)
Từ (1,2) suy ra M, N, P thẳng hàng
Muốn giải đáp các thắc mắc tới toán , vật lý vui lòng chat trức tiếp
Đúng 2
Bình luận (0)
x^2-6x+8=0
Mn giúp mình giải bài này thành nhiều cách đi mình đang cần gấp
Mình biết làm 1 cách thui, mong bạn thông cảm nha!
\(x^2-6x+8=0\Leftrightarrow x^2-2x-4x+8=0\)
\(\Leftrightarrow x\left(x-2\right)-4\left(x-2\right)=0\Leftrightarrow\left(x-2\right)\left(x-4\right)=0\)
\(\Leftrightarrow\hept{\begin{cases}x-2=0\\x-4=0\end{cases}\Leftrightarrow\hept{\begin{cases}x=2\\x=4\end{cases}}}\)
Chúc may mắn nha!
Đúng 0
Bình luận (0)

Mn làm giúp mình bài 8 với ạ mình đang cần gấp cảm ơn mn rất nhiều( giải thích chi tiết ạ).
Các số được điền vào các ô theo thứ tự từ trái sang phải là:
-1; - \(\dfrac{1}{3}\); \(\dfrac{2}{3}\); \(\dfrac{4}{3}\)
Đúng 0
Bình luận (0)
Mn ơi giải giúp mình bài hình này nhé khoảng tầm 22h mình quay lại lấy nha mai đi học r mình đang cần gấp cảm ơn mn 
a) Xét ΔOBH và ΔODA có
OB=OD(gt)
\(\widehat{BOH}=\widehat{DOA}\)(hai góc đối đỉnh)
OH=OA(O là trung điểm của HA)
Do đó: ΔOBH=ΔODA(c-g-c)
Suy ra: \(\widehat{OHB}=\widehat{OAD}\)(hai góc tương ứng)
mà \(\widehat{OHB}=90^0\)(gt)
nên \(\widehat{OAD}=90^0\)
hay AH\(\perp\)AD(đpcm)
b) Xét ΔAOE vuông tại A và ΔHOC vuông tại H có
OA=OH(O là trung điểm của AH)
\(\widehat{AOE}=\widehat{HOC}\)(hai góc đối đỉnh)
Do đó: ΔAOE=ΔHOC(Cạnh góc vuông-góc nhọn kề)
Suy ra: AE=HC(hai cạnh tương ứng)(1)
Ta có: ΔAOD=ΔHOB(cmt)
nên AD=HB(Hai cạnh tương ứng)(2)
Xét ΔAHB vuông tại H và ΔAHC vuông tại H có
AB=AC(ΔABC cân tại A)
AH chung
Do đó: ΔAHB=ΔAHC(Cạnh huyền-cạnh góc vuông)
Suy ra: HB=HC(Hai cạnh tương ứng)(3)
Từ (1), (2) và (3) suy ra AD=AE
mà E,A,D thẳng hàng(gt)
nên A là trung điểm của DE
Đúng 1
Bình luận (0)
) Xét ΔOBH và ΔODA có
OB=OD(gt)
ˆBOH=ˆDOABOH^=DOA^(hai góc đối đỉnh)
OH=OA(O là trung điểm của HA)
Do đó: ΔOBH=ΔODA(c-g-c)
Suy ra: ˆOHB=ˆOADOHB^=OAD^(hai góc tương ứng)
mà ˆOHB=900OHB^=900(gt)
nên ˆOAD=900OAD^=900
hay AH⊥⊥AD(đpcm)
b) Xét ΔAOE vuông tại A và ΔHOC vuông tại H có
OA=OH(O là trung điểm của AH)
ˆAOE=ˆHOCAOE^=HOC^(hai góc đối đỉnh)
Do đó: ΔAOE=ΔHOC(Cạnh góc vuông-góc nhọn kề)
Suy ra: AE=HC(hai cạnh tương ứng)(1)
Ta có: ΔAOD=ΔHOB(cmt)
nên AD=HB(Hai cạnh tương ứng)(2)
Xét ΔAHB vuông tại H và ΔAHC vuông tại H có
AB=AC(ΔABC cân tại A)
AH chung
Do đó: ΔAHB=ΔAHC(Cạnh huyền-cạnh góc vuông)
Suy ra: HB=HC(Hai cạnh tương ứng)(3)
Từ (1), (2) và (3) suy ra AD=AE
mà E,A,D thẳng hàng(gt)
nên A là trung điểm của DE
Đúng 0
Bình luận (0)
Mn ơi giải giúp mình bài hình nhé mình đang cần gấp khoảng tầm 21h00 mình quay lại lấy nhé nếu mà nhanh nhất thì cgx đc cảm ơn mn
Bài 3:
a) Ta có: \(A-\left(9x^3+8x^2-2x-7\right)=-9x^3-8x^2+5x+11\)
\(\Leftrightarrow A=-9x^3-8x^2+5x+11+9x^3+8x^2-2x-7\)
\(\Leftrightarrow A=3x+4\)
b) Đặt A(x)=0
nên 3x+4=0
hay \(x=-\dfrac{4}{3}\)
Đúng 1
Bình luận (1)
Giúp mình bài 2 với Mn ơi
Mình cần gấp!!! 
Bài 2:
a: Xét ΔABC có
BI,CI là các đường phân giác
BI cắt CI tại I
Do đó: I là tâm đường tròn nội tiếp ΔABC
b: Ta có: \(\widehat{DIB}=\widehat{IBC}\)(hai góc so le trong, DI//BC)
\(\widehat{DBI}=\widehat{IBC}\)(BI là phân giác của góc DBC)
Do đó: \(\widehat{DIB}=\widehat{DBI}\)
=>ΔDIB cân tại D
c: Ta có: \(\widehat{EIC}=\widehat{ICB}\)(hai góc so le trong, EI//BC)
\(\widehat{ECI}=\widehat{ICB}\)(CI là phân giác của góc ECB)
Do đó: \(\widehat{EIC}=\widehat{ECI}\)
=>ΔEIC cân tại E
d: Ta có: ΔDIB cân tại D
=>DB=DI
Ta có: ΔEIC cân tại E
=>EI=EC
Ta có: DI+IE=DE
mà DI=DB
và EC=EI
nên DB+EC=DE
Bài 1:
a: Xét ΔABC có
BE,CF là các đường phân giác
BE cắt CF tại I
Do đó: I là tâm đường tròn nội tiếp ΔABC
=>AI là phân giác của góc BAC
b: ta có: \(\widehat{ABE}=\widehat{CBE}=\dfrac{\widehat{ABC}}{2}\)(BE là phân giác của góc ABC)
\(\widehat{ACF}=\widehat{FCB}=\dfrac{\widehat{ACB}}{2}\)(CF là phân giác của góc ACB)
mà \(\widehat{ABC}=\widehat{ACB}\)
nên \(\widehat{ABE}=\widehat{EBC}=\widehat{ACF}=\widehat{FCB}\)
c: ta có: \(\widehat{EBC}=\widehat{FCB}\)
=>\(\widehat{IBC}=\widehat{ICB}\)
=>ΔIBC cân tại I
d: Xét ΔABE và ΔACF có
\(\widehat{ABE}=\widehat{ACF}\)
AB=AC
\(\widehat{BAE}\) chung
Do đó: ΔABE=ΔACF
=>BE=CF
e:
Ta có: ΔAEB=ΔAFC
=>AE=AF
Ta có: AE+EC+AC
AF+FB=AB
mà AE=AF
và AC=AB
nên EC=FB
Xét ΔFIB và ΔEIC có
FB=EC
\(\widehat{FBI}=\widehat{ECI}\)
BI=CI
Do đó: ΔFIB=ΔEIC
Đúng 0
Bình luận (0)
Mn ơi giải giúp mình bài này với
S=1/2*3/4*5/6*.....*99/10. Tìm phần nguyên của 19S
Mình đang cần gấp. Ai giải nhanh dùm mình thì mình tick dấu cho nha
















