Một bàn quay của thợ nặn đồ gốm quay đều với vận tốc góc 30 vòng trong một phút . Tìm chu kỳ quay và tốc độ dài của điểm cách tâm quay 20 cm ?
HELP ME !!!!!!!
Một bánh xe bán kính 60 cm quay đều 100 vòng trong thời gian 2 s. Tìm: 1. Tần số và chu kỳ quay. 2. Vận tốc góc và vận tốc dài của một điểm trên vành bánh xe. 3. Gia tốc hướng tâm của một điểm trên nằm trên vành bánh xe.
1.Bánh xe quay đều 100 vòng trong thời gian 2s\(\Rightarrow\) \(f=\dfrac{2}{100}=0,02\)vòng/s
Tần số quay của bánh xe: \(f=50\) vòng/s
Chu kì quay: \(T=\dfrac{1}{f}=\dfrac{1}{50}s\)
2.Vận tốc góc của 1 điểm trên vành bánh xe: \(\omega=\dfrac{2\pi}{T}=100\pi\) rad/s
Vận tốc dài của 1 điểm trên vành bánh xe: \(v=\omega.r=100\pi.0,6=60\pi\) m/s
3. Gia tốc hướng tâm của 1 điểm trên vành bánh xe:
\(a_{ht}=\dfrac{v^2}{r}=\dfrac{\left(60\pi\right)^2}{0,6}\approx59217,63\) m/s2
Một đĩa tròn bán kính 20 cm quay đều quanh trục của nó. Đĩa quay hết một vòng mất 0,2 s. Tìm tốc độ dài v, tốc độ góc ω và gia tốc hướng tâm aht của một điểm nằm trên mép đĩa và cách tâm một khoảng bằng bán kính của đĩa
A. v = 62,8m/s, ω = 31,4rad/s, a h t ≈ 19,7m/ s 2
B. v = 3,14m/s, ω = 15,7rad/s, a h t ≈ 49m/ s 2
C. v = 6,28m/s, ω = 31,4rad/s, a h t ≈ 197m/ s 2
D. v = 6,28m/s, ω = 3,14rad/s, a h t ≈ 97m/ s 2 .
Chọn đáp án C
+ Tốc độ góc: 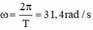
+ Tốc độ dài: ![]()
+ Gia tốc hướng tâm: ![]()
Một đĩa tròn có đường kính 40cm, quay đều, biết 1 phút nó quay được 30 vòng. Tính gia tốc hướng tâm của một điểm A nằm trên vành đĩa và tốc độ góc, tốc độ dài.
Một đĩa tròn có đường kính 40cm, quay đều, biết 1 phút nó quay được 30 vòng. Tính gia tốc hướng tâm của một điểm A nằm trên vành đĩa và tốc độ góc, tốc độ dài.
Đổi 40 cm=0,4 m ; 1 phút =60s
Tốc độ dài của điểm A nằm trên vành đĩa
\(v=2\pi\cdot r\cdot f=2\pi\cdot r\cdot\dfrac{N}{t}=2\pi\cdot0,4\cdot\dfrac{30}{60}=0,4\pi\left(\dfrac{m}{s}\right)\)
Gia tốc hướng tâm của điểm A nằm trên vành đĩa
\(a_{ht}=\dfrac{v^2}{r}=\dfrac{\left(0,4\pi\right)^2}{0,4}=0,4\pi^2\left(\dfrac{m}{s^2}\right)\)
Tốc độ góc của của điểm A nằm trên vành đĩa
\(\omega=\dfrac{v}{r}=\dfrac{0,4\pi}{0,4}=\pi\left(\dfrac{rad}{s}\right)\)
Một đĩa tròn bán kính 50 cm quay đều quanh trục đi qua tâm và vuông góc với đĩa. Đĩa quay 50 vòng trong 20 s. Tốc độ dài của một điểm nằm trên mép đĩa bằng
A. 3,28 m/s.
B. 6,23 m/s.
C. 7,85 m/s.
D. 8,91 m/s.
Đáp án C
Tốc độ góc:
![]()
Tốc độ dài của điểm ở mép đĩa:![]()
Một đĩa tròn bán kính 50 cm quay đều quanh trục đi qua tâm và vuông góc với đĩa. Đĩa quay 50 vòng trong 20 s. Tốc độ dài của một điểm nằm trên mép đĩa bằng
A. 3,28 m/s.
B. 6,23 m/s.
C. 7,85 m/s.
D. 8,91 m/s.
Chọn C.
Tốc độ góc ω = 50.2π /20= 5π rad/s
Tốc độ dài của điểm ở mép đĩa: v = ωr = 5π.0,5 ≈ 7,85 m/s.
Một đĩa tròn bán kính 50 cm quay đều quanh trục đi qua tâm và vuông góc với đĩa Đĩa quay 50 vòng trong 20 s. Tốc độ dài của một điểm nằm trên mép đĩa bằng
A. 3,28 m/s.
B. 6,23 m/s.
C. 7,85 m/s.
D. 8,91m/s.
Chọn đáp án C
+ Chu kì quay của đĩa: ![]()
+ Tốc độ góc: ![]()
+ Tốc độ dài: ![]()
Một đĩa tròn bán kính 50 cm quay đều quanh trục đi qua tâm và vuông góc với đĩa. Đĩa quay 50 vòng trong 20 s. Tốc độ dài của một điểm nằm trên mép đĩa bằng
A. 3,28 m/s.
B. 6,23 m/s
C. 7,85 m/s
D. 8,91 m/s
Chọn C.
Tốc độ góc
ω = 50 . 2 π 20 = 5 π rad / s
Tốc độ dài của điểm ở mép đĩa: v = ωr = 5π.0,5 ≈ 7,85 m/s.
5) Một đĩa hát có đường kính 10 cm quay đều với tần số 100 Hz.
a. Tính tốc độ góc, chu kỳ quay và tốc độ dài của đĩa.
b. Tính gia tốc hướng tâm .
a/ \(\omega=2\pi f=100\pi\left(rad\backslash s\right)\)
\(T=\dfrac{1}{f}=\dfrac{1}{100}\left(s\right)\)
b/ \(r=\dfrac{d}{2}=0,05\left(m\right)\)
\(v=r.2\pi f=10\pi\left(m\backslash s\right)\)