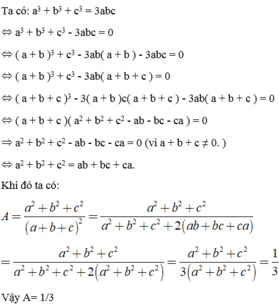Biết a+b+c=3. Tính Q=(a^3+b^3+c^3-3abc)/((a-b)^2+(b-c)^2+(c-a)^2)

Những câu hỏi liên quan
Cho a+b+c\(a^3+b^3+c^3=3abc\) áp dụng tính B=\(\frac{\left(a^2-b^2\right)^3+\left(b^2-c^2\right)^3+\left(c^2-a^2\right)^3}{\left(a-b\right)^3+\left(b-c\right)^3+\left(c-a\right)^3}\)
a+b+c=0.cmr a^3+b^3+c^3=3abc
em chứng minh thế này được không các thầy (cô) giáo
a+b+c=0
=>a+b=-c
=>a+b=3abc/-3ab
=>(a+b).(-3ab)=3abc
=>(a+b).(a^2-ab+b^2-a^2-2ab-b^2)=3abc
=>(a+b)(a^2-ab+b^2)-(a+b).(a^2+2ab+b^2)=3abc
=>a^3+b^3-(a+b)^3=3abc
mà a+b=-c=> a^3+b^3-(-c)^3=3abc
=>a^3+b^3+c^3=3abc
Được bạn nhé :"))))
Ủng hộ mình = cách theo dõi mình nha
Đúng 0
Bình luận (1)
a+b+c=0
\(\left(a+b+c\right)^3=0\)
\(\Leftrightarrow a^3+b^3+c^3+3a^2b+3ab^2+3a^2c+3ac^2+3b^2c+3bc^2+6abc=0\)
\(\Leftrightarrow a^3+b^3+c^3+\left(3a^2b+3ab^2+3abc\right)+\left(3a^2c+3ac^2+3abc\right)+\left(3bc^2+3b^2c+3abc\right)-3abc=0\)\(\Leftrightarrow a^3+b^3+c^3+3ab\left(a+b+c\right)+3ac\left(a+b+c\right)+3bc\left(a+b+c\right)-3abc=0\)\(\Leftrightarrow a^3+b^3+c^3-3abc=0\)
\(\Leftrightarrow a^3+b^3+c^3=3abc\)
mk ko chắc cách bn đúng nhưng cách của mk là phù hợp nhất đó
Đúng 0
Bình luận (0)
Không nên chứng minh như thế này nhé. Ở ngay phần \(a+b=\frac{3abc}{-3ab}\) đã sai sót vì bạn không tính đến trường hợp \(a=0\) hoặc $b=0$ đã thực hiện phép chia như vậy.
Sử dụng hằng đẳng thức: \((a+b)^3=a^3+b^3+3ab(a+b)\) ta có:
\(a^3+b^3+c^3=(a+b)^3-3ab(a+b)+c^3\)
Vì \(a+b+c=0\Rightarrow a+b=-c\). Thay vào biểu thức trên:
\((a+b)^3-3ab(a+b)+c^3=(-c)^3-3ab(-c)+c^3=-c^3+3abc+c^3=3abc\)
Do đó:
\(a^3+b^3+c^3=3abc\)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Cho a^3 + b^3 +c^3 =3abc , a + b+ c\(\ne\)0
Tính B=\(\frac{a^2+b^2+c^2}{\left(a+b+c\right)^2}\)
Ta có: a3 + b3 + c3 = 3abc
<=> (a + b)(a2 - ab + b2) + c3 - 3abc = 0
<=> (a + b)3 - 3ab(a + b) + c3 - 3abc = 0
<=> (a + b + c)[(a + b)2 - (a + b)c + c2) - 3ab(a + b + c) = 0
<=> (a + b + c)(a2 + 2ab + b2 - ac - bc + c2 - 3ab) = 0
<=> (a + b + c)(a2 + b2 + c2 - ab - ac - bc) = 0
<=> \(\orbr{\begin{cases}a+b+c=0\left(loại\right)\\a^2+b^2+c^2-ab-ac-bc=0\end{cases}}\)
<=> 2a2 + 2b2 + 2c2 - 2ab - 2ac - 2bc = 0
<= > (a2 - 2ab + b2) + (b2 - 2bc + c2) + (c2 - 2ac + a2) = 0
<=> (a - b)2 + (b - c)2 + (c - a)2 = 0
<=> \(\hept{\begin{cases}a-b=0\\b-c=0\\c-a=0\end{cases}}\)<=> a = b = c
Khi đó: B = \(\frac{a^2+a^2+a^2}{\left(a+a+a\right)^2}=\frac{3a^2}{\left(3a\right)^2}=\frac{3a^2}{9a^2}=\frac{1}{3}\)
ta có a3+b3+c3=3abc <=> a3+b3+c3-3abc=0
<=> (a+b)3-3ab(a+b)+c3-3abc=0
<=> (a+b+c)3-3(a+b)c(a+b+c)-3ab(a+b+c)=0
<=> (a+b+c)(a2+b2+c2-ab-bc-ca)=0
<=> a2+b2+c2-ab-bc-ca=0 (vì a+b+c=0)
<=> (a-b)2+(b-c)2+(c-a)2=0
<=> a=b=c
khi đó \(B=\frac{a^2+b^2+c^2}{\left(a+b+c\right)^2}=\frac{a^2+a^2+a^2}{\left(a+a+a\right)^2}=\frac{3a^2}{\left(3a\right)^2}=\frac{1}{3}\)
1. Cho a2 - b2 - c2 =3abc
Tính H = \(\left(1-\frac{a}{b}\right)\left(1-\frac{b}{c}\right)\left(1-\frac{c}{a}\right)\)
2. Cho a - b + c = - 4
Tính B = \(\frac{a^3-b^3+c^3+3abc}{\left(a+b\right)^2+\left(b+c\right)^2+\left(c-a\right)^2}\)
cho a^3+b^3+c^3=3abc=21 tính a(b^2+c^2)+b(c^2+a^2)+c(a^2+b^2)
vào trang cá nhân của mình đi mà, mình có trả lời r đó
Đúng 0
Bình luận (0)
Áp dụng a^3+b^3+c^3+3abc=(a+b+c)(a^2+b^2+c^2-ab-ac-bc)
Biết 1/a+1/b+1/c=0
Tính A=bc/a^2 + ca/b^2 +ab/c^2
Ta có
\(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}=\frac{bc+ac+ab}{abc}=0\Rightarrow ab+bc+ac=0.\)
\(A=\frac{\left(bc\right)^3+\left(ac\right)^3+\left(ab\right)^3}{\left(abc\right)^2}\)
Ta có
\(\left(ab\right)^3+\left(bc\right)^3+\left(ac\right)^3-3\left(abc\right)^2=\)
\(=\left(ab+bc+ac\right)\left[\left(ab\right)^2+\left(bc\right)^2+\left(ac\right)^2-abbc-bcac-abac\right]=0\)
\(\Rightarrow\left(ab\right)^3+\left(bc\right)^3+\left(ac\right)^3=3\left(abc\right)^2\)
\(\Rightarrow A=\frac{3\left(abc\right)^2}{\left(abc\right)^2}=3\)
Cho a^3+b^3+c^3= 3abc và a+b+c khác 0.
Xem chi tiết
Tính : A = a\(^2\) + b\(^2\)+ c\(^2\)/ (a+b+c)^2
ta có: a3 + b3 + c3 = 3abc
=> a3 + b3 + c3 - 3abc = (a+b+c).(a2 + b2 + c2 - ab - bc -ac) = 0
mà a + b + c khác 0
=> a2 + b2 + c2 - ab - bc - ac = 0
=> a = b = c
\(\Rightarrow A=\frac{a^2+b^2+c^2}{\left(a+b+c\right)^2}=\frac{a^2+a^2+a^2}{\left(a+a+a\right)^2}=\frac{3a^2}{\left(3a\right)^2}=\frac{3a^2}{3^2.a^2}=\frac{1}{3}.\)
Đúng 0
Bình luận (0)
Câu 1: CMR : Nếu a^3+b^3+c^33abc thì a+b+c0 hoặc abc Câu 2: Cho frac{1}{a}+frac{1}{b}+frac{1}{c}0 . Tính frac{bc}{a^2}+frac{ca}{b^2}+frac{ab}{c^2}Câu 3 : Cho a^3+b^3+c^33abcleft(a.b.cne0right). TínhAleft(1+frac{a}{b}right)left(1+frac{b}{c}right)left(1+frac{c}{a}right)
Đọc tiếp
Câu 1: CMR : Nếu \(a^3+b^3+c^3=3abc\) thì \(a+b+c=0\) hoặc \(a=b=c\)
Câu 2: Cho \(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}=0\) . Tính \(\frac{bc}{a^2}+\frac{ca}{b^2}+\frac{ab}{c^2}\)
Câu 3 : Cho \(a^3+b^3+c^3=3abc\left(a.b.c\ne0\right)\). Tính\(A=\left(1+\frac{a}{b}\right)\left(1+\frac{b}{c}\right)\left(1+\frac{c}{a}\right)\)
Câu 1:
Chứng minh a3+b3+c3=3abc thì a+b+c=0\(a^3+b^3+c^3=3abc\Rightarrow a^3+b^3+c^3-3abc=0\)
\(\Rightarrow\left(a+b\right)^3-3a^2b-3ab^2+c^3-3abc=0\)
\(\Rightarrow\left[\left(a+b\right)^3+c^3\right]-3abc\left(a+b+c\right)=0\)
\(\Rightarrow\left(a+b+c\right)\left[\left(a+b\right)^2-\left(a+b\right)c+c^2\right]-3ab\left(a+b+c\right)=0\)
\(\Rightarrow0=0\) Đúng (Đpcm)
Chứng minh a3+b3+c3=3abc thì a=b=cÁp dụng Bđt Cô si 3 số ta có:
\(a^3+b^3+c^3\ge3\sqrt[3]{a^3b^3c^3}=3abc\)
Dấu = khi a=b=c (Đpcm)
Đúng 0
Bình luận (0)
Câu 2
Từ \(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}=0\Rightarrow\frac{1}{a^3}+\frac{1}{b^3}+\frac{1}{c^3}=3\cdot\frac{1}{abc}\)
Ta có:
\(\frac{ab}{c^2}+\frac{bc}{a^2}+\frac{ac}{b^2}=\frac{abc}{c^3}+\frac{abc}{a^3}+\frac{abc}{b^3}\)
\(=abc\left(\frac{1}{a^3}+\frac{1}{b^3}+\frac{1}{c^3}\right)\)
\(=abc\cdot3\cdot\frac{1}{abc}=3\)
Đúng 0
Bình luận (0)
\(a^3+b^3+c^3=3abc\)
\(\Leftrightarrow\left(a+b+c\right)\left(a^2+b^2+c^2-ab-bc-ac\right)=0\)
\(\Leftrightarrow\left[\begin{array}{nghiempt}a+b+c=0\\a^2+b^2+c^2-ab-bc-ac=0\end{array}\right.\)
Xét \(a+b+c=0\)\(\Rightarrow\begin{cases}a=-\left(b+c\right)\\b=-\left(a+c\right)\\c=-\left(a+b\right)\end{cases}\)\(\Rightarrow A=\left(1-\frac{b+c}{b}\right)\left(1-\frac{a+c}{c}\right)\left(1-\frac{a+b}{a}\right)\)
\(=\left(1-1-\frac{c}{b}\right)\left(1-1-\frac{a}{c}\right)\left(1-1-\frac{b}{a}\right)\)
\(=\left(-\frac{c}{b}\right)\left(-\frac{a}{c}\right)\left(-\frac{b}{a}\right)=-1\)
Xét \(a^2+b^2+c^2-ab-bc-ca=0\)\(\Leftrightarrow\left(a-b\right)^2+\left(b-c\right)^2+\left(c-a\right)^2=0\)
\(\Leftrightarrow a-b=b-c=c-a=0\Leftrightarrow a=b=c\)
\(\Leftrightarrow A=\left(1+1\right)\left(1+1\right)\left(1+1\right)=8\)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Cho 3 số abc thỏa mãn :\(a^3+b^3+c^3=3abc\)a;b;c đôi một khác nhau
Tính GTBT:
\(B=\frac{1}{a^2+b^2+-c^2}+\frac{1}{b^2+c^2-a^2}+\frac{1}{c^2+a^2-b^2}\)