Cho tam giác ABC có trọng tâm G, trung tuyến AM . Gọi I là điểm trên cạnh BC sao
cho CI IB

Những câu hỏi liên quan
Cho tam giác ABC có trung tuyến AM. Lấy điểm G trên AM sao cho AG = 2GM
a) Chứng minh rằng G là trọng tâm của tam giác ABC
b) Gọi D, E, F lần lượt là hính chiếu của G trên các cạnh BC, CA, AB. Chứng minh rằng G cũng là trọng tâm của tam giác DEF
Cho tam giác ABC lấy điểm M trên cạnh BC sao cho BM = 3MC. Gọi I là trung điểm của BC va G la trọng tâm của tam giac ABC. Tính vecto AM theo vecto AG va vecto BC
Cho tam giác ABC(AB<AC) và AM là trung tuyến. Gọi G là trọng tâm của tam giác ABC, trên tia AM lấy điểm G' sao cho G là trung điểm của AC'
a) Chứng minh MG' = \(\frac{1}{2}\)AG
b) Chứng minh BG'=GC
c)Đường trung trực của cạnh BC lần lượt cắt các cạnh AC,Cg tại I và k. Chứng minh tam giác ICK = tam giác IBK
Hình như là điểm C đó cậu.Chắc mình gõ nhầm
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Cho tam giác ABC có đường trung tuyến AM,gọi G là trọng tâm tam giác,trên tia AM lấy điểm D,sao cho G là trung điểm của AD.Chứng minh:MG=MD và BĐ=CG
Ta có: G là trọng tâm của tam giác
suy ra: MG=1/2AM,suy ra: MG=1/2AG
mà AG=GD suy ra: MG=1/2GD -> MG=MD( điều phải cm)
2. xét tam giác BDM và tam giác CGM
góc GMC=góc DMB (đối đỉnh); GM=MD (cm trên); BM=CM (AM là trung tuyến)
-> tam giác BDM = tam giác CGM(c.g.c)
-> BD=CG (dpcm)
Đúng 0
Bình luận (0)
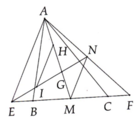
Cho tam giác ABC, trung tuyến AM và trọng tâm G. Trên tia đối của tia BC lấy điểm E, trên tia đối của tia CB lấy điểm F sao cho BE CF.a) Chứng minh G là trọng tâm tam giác AEF.b) Gọi N là trung điểm của AF. Chứng minh ba điểm E, G, N thẳng hàng.c) Gọi H là trung điểm của GA, I là trung điểm GE. Chứng minh IH // MN và IH MN.
Đọc tiếp
Cho tam giác ABC, trung tuyến AM và trọng tâm G. Trên tia đối của tia BC lấy điểm E, trên tia đối của tia CB lấy điểm F sao cho BE = CF.
a) Chứng minh G là trọng tâm tam giác AEF.
b) Gọi N là trung điểm của AF. Chứng minh ba điểm E, G, N thẳng hàng.
c) Gọi H là trung điểm của GA, I là trung điểm GE. Chứng minh IH // MN và IH = MN.
Cho tam giác ABC. Vẽ trung tuyến BM. Trên tia BM lấy hai điểm G, K sao cho
B
G
2
3
B
M
và G là trung điểm của BK. Gọi E là trung điểm CK; GE cắt AC tại I Chứng minh:a) I là trọng tâm của tam giác KGC;b)
C
I
1
3
A
C
.
Đọc tiếp
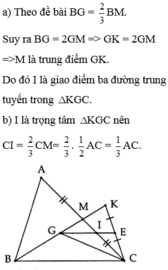
Cho tam giác ABC. Vẽ trung tuyến BM. Trên tia BM lấy hai điểm G, K sao cho B G = 2 3 B M và G là trung điểm của BK. Gọi E là trung điểm CK; GE cắt AC tại I Chứng minh:
a) I là trọng tâm của tam giác KGC;
b) C I = 1 3 A C .
cho tam giác ABC có đường trung tuyến am. trên tia đối của tia MA lấy điểm D. gọi G là trọng tâm của tam giác abc, cho biết MD= MG.
a. chứng mình BG song song CD
b.gọi I là trọng tâm của bd. H là giao điểm của AI và BM. chứng mình AM= 2 lần AI
a: Xét tứ giác BGCD có
M là trung điểm chung của BC và GD
=>BGCD là hình bình hành
=>BG//CD
Đúng 0
Bình luận (0)
Tam giác ABC có trung tuyến BD. Trên tia đối của tia DB lấy điểm E sao cho DE=DB.
a) CMR: BC//AE
b) Gọi M; N theo thứ tự là trung điểm của BC và CE. I là giao điểm của AM với BE. CMR : I là trọng tâm của tam giác ABC
a: Xét tứ giác ABCE có
D là trung điểm của AC
D là trung điểm của BE
Do đó; ABCE là hình bình hành
Suy ra: BC//AE
b: Xét ΔABC có
AM là đường trung tuyến
BD là đường trung tuyến
AM cắt BD tại I
Do đó: I là trọng tâm của ΔABC
Đúng 0
Bình luận (0)
Cho tam giác ABC,trung tuyến AM và trọng tâm G.Trên tia đối của tia BC lấy điểm E,trên tia đối của tia BC lấy điểm E,trên tia đối của tia CB lấy điểm F sao cho BE=CF
a)chứng minh G là trọng tâm tam giác AEF
b)Gọi N là trung điểm của AF.chứng minh ba điểm E,G,N thẳng hàng
c)Gọi H là trung điểm của G,A,I là trung điểm của GE.Chứng minh IH song song với MN và IH=MN
a: BM+BE=ME
MC+CF=MF
mà BM=MC và BE=CF
nên ME=MF
Xét ΔAEF có
AM là trung tuyến
AG=2/3AM
=>G là trọng tâm
b: Xét ΔAEF có
EN là trung tuyến
G là trọng tâm
=>E,G,N thẳng hàng
c: Xét ΔGAE có GH/GA=GI/GE
nên IH//AE và IH=1/2AE
=>IH//MN và IH=MN
Đúng 0
Bình luận (0)