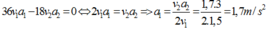cho phương trình vận tốc của vật v1= -4t+5 (m/s) tính gia tốc và vận tốc của mỗi vật

Những câu hỏi liên quan
cho phương trình chuyển động của chất điểm là : x = 2+10t+4t^2, với x có đơn vị là m, t có đơn vị là s. Xác định : a.Tọa độ ban đầu, vận tốc ban đầu, gia tốc của vật b.Viết công thức vận tốc của vật, tính vận tốc khi t = 5 c.Sau khi chuyển động 2s thì vật ở vị trí nào
a. Tọa độ ban đầu là 2m, vận tốc ban đầu là 10m/s, gia tốc là 8m/s2
b. Công thức vận tốc là v=v0+at=10+8t
Khi t=5s thì v=10+8.5= 50 (m/s)
c. x= 2+10.2+4.22 = 38 (m)
Vật ở vị trí cách gốc tọa độ 38m
Đúng 1
Bình luận (0)
1 vật chuyển động theo phương trình : x4t^2 +20t ( vs x đo bằng cm, t đo s) a) xác định vận tốc đầu và gia tốc của vật b) xác định vận tốc và vị trí của vật tại thời điểm t2s c) tính quãng đường đi được trong khoảng thời gian t5s kể từ khi bắt đầu chuyển độngd) tính quãng đường vật đi được từ t12s đến t25s. Tính vận tốc trung bình trong khoảng thời gian này
Đọc tiếp
1 vật chuyển động theo phương trình : x=4t^2 +20t ( vs x đo bằng cm, t đo = s)
a) xác định vận tốc đầu và gia tốc của vật
b) xác định vận tốc và vị trí của vật tại thời điểm t=2s
c) tính quãng đường đi được trong khoảng thời gian t=5s kể từ khi bắt đầu chuyển động
d) tính quãng đường vật đi được từ t1=2s đến t2=5s. Tính vận tốc trung bình trong khoảng thời gian này
a,Phương trình chuyển động của vật
\(x=4t^2+20t\left(cm,s\right)\Rightarrow a=8\left(\dfrac{cm}{s^2}\right);v_0=20\left(\dfrac{cm}{s}\right)\)
Vậy vận tốc ban đầu của vật là 20 cm/s và gia tốc của vật là 8 cm/s2
b, Vận tốc của vật ở thời điểm t=2s
\(v=20+8\cdot2=36\left(\dfrac{cm}{s}\right)\)
Vị trí của vật ở thời điểm t=2s cách gốc tọa độ 1 khoảng
\(x=4\cdot2^2+20\cdot2=56\left(cm\right)\)
c,Quãng đường đi được trong khoảng thời gian 5 s kể từ lúc chuyển động là
\(s=4\cdot5^2+20\cdot5=200\left(cm\right)\)
d Vận tốc trung bình trong khoảng thời gian từ t1=2s đến t2=5s
Ta có:\(x_1=4\cdot2^2+20\cdot2=56\left(cm\right)\)
\(x_2=4\cdot5^2+20\cdot5=200\left(cm\right)\)
\(v_{tb}=\dfrac{x_2-x_1}{t_2-t_1}=\dfrac{200-56}{5-2}=48\left(\dfrac{cm}{s}\right)\)
Đúng 1
Bình luận (1)
lần sau bạn đừng bôi đen nha rất khó nhìn
Đúng 0
Bình luận (0)
Phương trình vận tốc của một vật chuyển động thẳng là v = -3t +6 (v tính bằng m/s ; t tính bằng s)
a) Xác định gia tốc và vận tốc ban đầu
b) Viết pt chuyển động của vật
\(v=v_0+at\)\(=-3t+6\)
\(\Rightarrow v_0=6m\)/s và \(a=-3m\)/s2
Phương trình chuyển động của vật:
\(x=x_0+v_0t+\dfrac{1}{2}at^2=6t+\dfrac{1}{2}\cdot\left(-3\right)\cdot t^2=6t-\dfrac{3}{2}t^2\)
Đúng 1
Bình luận (0)
Một vật chuyển động thẳng biến đổi đều với phương trình chuyển động là:
x
20
+
4
t
+
t
2
( m;s )a. Hãy viết phương trình đường đi và phương trình vận tốc của vật ?b. Lúc t 4s, vật có tọa độ và vận tốc là bao nhiêu ?
Đọc tiếp
Một vật chuyển động thẳng biến đổi đều với phương trình chuyển động là: x = 20 + 4 t + t 2 ( m;s )
a. Hãy viết phương trình đường đi và phương trình vận tốc của vật ?
b. Lúc t = 4s, vật có tọa độ và vận tốc là bao nhiêu ?
Giải:
a. Ta có phương trình quãng đường: s = v 0 t + 1 2 a t 2
Theo bài ra: x = 20 + 4 t + t 2 ( m;s )
⇒ 1 2 a = 1 ⇒ a = 2 m / s 2 , v 0 = 4 ( m / s )
Vậy S = 4 t + t 2
Phương trình vận tốc v = v 0 + a t = 4 + 2 t m / s
b. Lúc t = 4s, vật có tọa độ x = 20 + 4.4 + 4 2 = 52 m
Vận tốc là v = 4 + 2.4 = 10 m / s
Đúng 0
Bình luận (1)
Dựa vào các đồ thị trong Hình 2.3:a) Viết phương trình li độ, vận tốc và gia tốc của vật dao động điều hòa.b) Mô tả định tính tính chất của li độ, vận tốc và gia tốc của vật tại các thười điểm 0,5 s; 0,75 s và 1 sc) Dựa vào các phương trình được xây dựng ở câu a để kiểm chứng lại mô tả định tính ở câu b
Đọc tiếp
Dựa vào các đồ thị trong Hình 2.3:
a) Viết phương trình li độ, vận tốc và gia tốc của vật dao động điều hòa.
b) Mô tả định tính tính chất của li độ, vận tốc và gia tốc của vật tại các thười điểm 0,5 s; 0,75 s và 1 s
c) Dựa vào các phương trình được xây dựng ở câu a để kiểm chứng lại mô tả định tính ở câu b
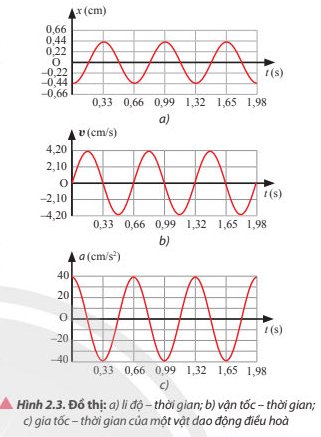
Biên độ dao động: A = 0,44 cm
Tốc độ cực đại: vmax = 4,2 cm/s
Gia tốc cực đại: amax = 40 cm/s2
Chu kì của gia tốc của vật: T = 0,66 s.
Tốc độ góc: \(\omega = \frac{{2\pi }}{T} = \frac{{100}}{{33}}\pi (rad/s)\)
a) Tại thời điểm ban đầu vật đi từ biên âm tiến về VTCB nên pha ban đầu φ0 = π(rad)
Khi đó, phương trình li độ có dạng:
x = Acos(ωt+φ0) = 0,44cos(\(\frac{{100\pi }}{{33}}\)t+π) (cm)
Phương trình vận tốc có dạng:
v = ωAcos(ωt+φ0+\(\frac{\pi }{2}\)) = 4,2cos(\(\frac{{100\pi }}{{33}}\)t+\(\frac{{3\pi }}{2}\)) (cm/s)
Phương trình gia tốc có dạng:
a = −ω2Acos(ωt+φ0) = −40cos(\(\frac{{100\pi }}{{33}}\)t+π) (cm/s2)
b)
Từ đồ thị có thể thấy:
t= 0,33s: x=0,44 cm; v=0 cm/s; a=-40 cm/s2
t= 0,495s: x=0 cm; v=-4,2 cm/s; a=0 cm/s2
t= 0,66s: x=-0,44 cm; v=0 cm/s; a=40 cm/s2
c) Nghiệm lại với các phương trình.
- Tại thời điểm t = 0,5 s
x = 0,44cos(\(\frac{{100\pi }}{{33}}\).0,5+π) = −0,02 (cm)
v =4,2cos(\(\frac{{100\pi }}{{33}}\).0,5+3π2) = −4,19 (cm/s)
a =−40cos(\(\frac{{100\pi }}{{33}}\).0,5+π) = 1,9 (cm/s2)
- Tại thời điểm t = 0,75 s
x = 0,44cos(\(\frac{{100\pi }}{{33}}\).0,75+π) = −0,29 (cm)
v = 4,2cos(\(\frac{{100\pi }}{{33}}\).0,75+\(\frac{{3\pi }}{2}\)) = 3,17 (cm/s)
a = −40cos(\(\frac{{100\pi }}{{33}}\).0,75+π) = 26,2 (cm/s2)
- Tại thời điểm t = 1 s
x = 0,44cos(\(\frac{{100\pi }}{{33}}\).1+π) = 0,438 (cm)
v = 4,2cos(\(\frac{{100\pi }}{{33}}\).1+3π2) = −0,4 (cm/s)
a = −40cos(\(\frac{{100\pi }}{{33}}\).1+π) = −39,8 (cm/s2)
Đúng 0
Bình luận (0)
Phương trình của một vật chuyển động thẳng là: x= 10 + 5t + 0,4t2 (m; s)
a/ Vận tốc ban đầu, gia tốc của chuyển động và cho biết tính chất của chuyển động.
b/ viết phương trìinh tổng quát của vận tốc
Phương trình chuyển động của một vật : x 5t2 + 20t + 50 (m, s)
a. Xác định vận tốc đầu và gia tốc của vật và nhận xét loại chuyển động?
b. Tìm vận tốc lúc 3s của vật?
c. Xác định vị trí của vật khi có vận tốc 40m/s
Đọc tiếp
Phương trình chuyển động của một vật : x = 5t2 + 20t + 50 (m, s)
a. Xác định vận tốc đầu và gia tốc của vật và nhận xét loại chuyển động?
b. Tìm vận tốc lúc 3s của vật?
c. Xác định vị trí của vật khi có vận tốc 40m/s
Hai vật dao động điều hòa. Ở thời điểm t gọi v1, v2 là vận tốc lần lượt của vật thứ nhất và vật thứ hai. Khi vận tốc của vật thứ nhất là v1 1,5m/s thì gia tốc của vật thứ hai là a2 3 m/s2 . Biết 18v12 - 9v22 14,5 (m/s)2. Độ lớn gia tốc của vật thứ nhất tại thời điểm trên là: A. a1 1,7 m/s2 B. a1 4 m/s2 C. a1 3 m/s2 D. a1 2 m/s2
Đọc tiếp
Hai vật dao động điều hòa. Ở thời điểm t gọi v1, v2 là vận tốc lần lượt của vật thứ nhất và vật thứ hai. Khi vận tốc của vật thứ nhất là v1 = 1,5m/s thì gia tốc của vật thứ hai là a2 = 3 m/s2 . Biết 18v12 - 9v22 = 14,5 (m/s)2. Độ lớn gia tốc của vật thứ nhất tại thời điểm trên là:
A. a1 = 1,7 m/s2
B. a1 = 4 m/s2
C. a1 = 3 m/s2
D. a1 = 2 m/s2
Phương trình chuyển động của một vật trên đường thẳng là : x = 2t2 + 10t +100 (m;s)
a. Tìm vận tốc, gia tốc, tọa độ ban đầu của vật. Nêu tính chất chuyển động. Tính vận tốc của vật lúc t=2s
b. Tính đường đi của vật khi vận tốc đạt 30m
\(x=2t^2+10t+100\)
a) v0=10m/s; a=4m/s2; x0=100m
Đây là chuyển động nhanh dần đều.
Vận tốc vật lúc t=2s: \(v=v_0+at=10+4\cdot2=18\)m/s
b) Quãng đường vật đi khi đạt vận tốc v=30m/s:
\(v^2-v_0^2=2aS\) \(\Rightarrow S=\dfrac{2a}{v^2-v_0^2}=\dfrac{2\cdot4}{30^2-10^2}=0,01m=1cm\)
Đúng 1
Bình luận (0)