cho a+b+c=2abc , 1/a+1/b+1/c=2 .tinh 1/a^2+1/b^2+1/c^2

Những câu hỏi liên quan
Bài 1:Cho 0<=a;b;c<=2.a+b+c=3
CM:3<=a^3+b^3+c^3-3(a-1)(b-1)(c-1)<=9
Bài 2: Cho -1<=a;b;c<=2.a+b+c=0.CM:
a,a^2+b^2+c^2<=6
b,2abc<=a^2+b^2+c^2<=2abc+2
c,a^2+b^2+c^2<=8-abc
Bài 1
Đặt \(A=a^3+b^3+c^3-3(a-1)(b-1)(c-1)\)
Biến đổi:
\(A=a^3+b^3+c^3-3[abc-(ab+bc+ac)+a+b+c-1]=a^3+b^3+c^3-3abc+3(ab+bc+ac)-6\)
\(A=(a+b+c)^3-3[(a+b)(b+c)(c+a)+abc]-6+3(ab+bc+ac)\)
\(A=21-3(a+b+c)(ab+bc+ac)+3(ab+bc+ac)=21-6(ab+bc+ac)\)
Áp dụng BĐT Am-Gm:
\(3(ab+bc+ac)\leq (a+b+c)^2=9\Rightarrow ab+bc+ac\leq 3\)
\(\Rightarrow A\geq 21-6.3=3\). Dấu bằng xảy ra khi $a=b=c=1$
Vì \(0\leq a,b,c\leq2\Rightarrow (a-2)(b-2)(c-2)\leq 0\)
\(\Leftrightarrow abc-2(ab+bc+ac)+4\leq 0\Leftrightarrow 2(ab+bc+ac)\geq 4+abc\geq 0\Rightarrow ab+bc+ac\geq 2\)
\(\Rightarrow A\leq 21-6.2=9\). Dấu bằng xảy ra khi $(a,b,c)=(0,1,2)$ và các hoán vị.
Đúng 0
Bình luận (0)
Bài 2a)
Ta có
\(A=a^2+b^2+c^2=(a+1)^2+(b+1)^2+(c+1)^2-3-2(a+b+c)\)
\(\Leftrightarrow A=(a+b+c+3)^2-2[(a+1)(b+1)+(b+1)(c+1)+(c+1)(a+1)]-3\)
\(\Leftrightarrow A=6-2[(a+1)(b+1)+(b+1)(c+1)+(c+1)(a+1)]\)
Vì \(-1\leq a,b,c\leq 2\Rightarrow a+1,b+1,c+1\geq 0\)
\(\Rightarrow (a+1)(b+1)+(b+1)(c+1)+(c+1)(a+1)\geq 0\Rightarrow A\leq 6\)
Dấu bằng xảy ra khi \((a,b,c)=(-1,-1,2)\) và các hoán vị của nó
Đúng 0
Bình luận (0)
Câu 2b)
Đặt \((a,b,c)\mapsto(x-1,y-1,z-1)\)
Khi đó ta có \(0\leq x,y,z\leq 3,x+y+z=3\)
Cần cm
\(2(x-1)(y-1)(z-1)\leq (x-1)^2+(y-1)^2+(z-1)^2\leq 2(x-1)(y-1)(z-1)+2\)
Vế đầu:
Khai triển kết hợp với $x+y+z=3$ thì \(\text{BĐT}\Leftrightarrow xyz\leq 1\)
Điều này đúng vì theo AM-GM cho số không âm thì \(3=x+y+z\geq 3\sqrt[3]{xyz}\rightarrow xyz\leq 1\)
Ta có đpcm. Dấu bằng xảy ra khi $x=y=z=1$ hay $a=b=c=0$
Vế sau:
Tương tự phần trên \(\text{BĐT}\Leftrightarrow xyz\geq 0\) ( luôn đúng do $x,y,z\geq 0$)
Dấu bằng xảy ra khi $(x,y,z)=(2,-1,-1)$ và hoán vị
Lưu ý: "Khi" khác với "khi và chỉ khi"- nghĩa là chỉ nêu 1TH chứ chưa quét hết toàn bộ điểm rơi
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
1.
Cho -1<=a;b;c<=2.a+b+c=0.CM:
a,a^2+b^2+c^2<=6
b,2abc<=a^2+b^2+c^2<=2abc+2
c,a^2+b^2+c^2<=8-abc
2,
Cho 0<=a;b;c<=2.a+b+c=3
CM:3<=a^3+b^3+c^3-3(a-1)(b-1)(c-1)<=9
Cho 1/a+1/b+1/c=3 và 1/a^2+1/b^2+1/c^2=5(abc khác 0).Chứng minh rằng a+b+c=2abc
cho a,b,c khác 0 thỏa mãn a^2017 b^2017 c^2017=1; a^2(b c) b^2(c a) c^2(a b) 2abc =0 tính 1/a^2017 1/b^2017 1/c^2017
Cho a, b, c > . Chứng minh rằng:
a, \(\dfrac{a^2}{b+c}+\dfrac{b^2}{c+a}+\dfrac{c^2}{a+b}\ge\dfrac{a+b+c}{2}\)
b, \(\dfrac{1}{a^2+bc}+\dfrac{1}{b^2+ac}+\dfrac{1}{c^2+ab}\le\dfrac{a+b+c}{2abc}\)
a.
Ta có: \(\dfrac{a^2}{b+c}+\dfrac{b+c}{4}\ge2\sqrt{\dfrac{a^2\left(b+c\right)}{4\left(b+c\right)}}=a\)
Tương tự: \(\dfrac{b^2}{c+a}+\dfrac{c+a}{4}\ge b\) ; \(\dfrac{c^2}{a+b}+\dfrac{a+b}{4}\ge c\)
Cộng vế:
\(\dfrac{a^2}{b+c}+\dfrac{b^2}{c+a}+\dfrac{c^2}{a+b}+\dfrac{a+b+c}{2}\ge a+b+c\)
\(\Leftrightarrow\dfrac{a^2}{b+c}+\dfrac{b^2}{c+a}+\dfrac{c^2}{a+b}\ge\dfrac{a+b+c}{2}\) (đpcm)
Dấu "=" xảy ra khi \(a=b=c\)
Đúng 0
Bình luận (0)
b.
Ta có:
\(a^2+bc\ge2\sqrt{a^2bc}=2\sqrt{ab.ac}\Rightarrow\dfrac{1}{a^2+bc}\le\dfrac{1}{2\sqrt{ab.ac}}\le\dfrac{1}{4}\left(\dfrac{1}{ab}+\dfrac{1}{ac}\right)\)
Tương tự: \(\dfrac{1}{b^2+ac}\le\dfrac{1}{4}\left(\dfrac{1}{ab}+\dfrac{1}{bc}\right)\) ; \(\dfrac{1}{c^2+ab}\le\dfrac{1}{4}\left(\dfrac{1}{ac}+\dfrac{1}{bc}\right)\)
Cộng vế với vế:
\(\dfrac{1}{a^2+bc}+\dfrac{1}{b^2+ac}+\dfrac{1}{c^2+ab}\le\dfrac{1}{2}\left(\dfrac{1}{ab}+\dfrac{1}{bc}+\dfrac{1}{ca}\right)=\dfrac{a+b+c}{2abc}\)
Dấu "=" xảy ra khi \(a=b=c\)
Đúng 0
Bình luận (0)
Cho a,b,c dương thỏa mãn \(a^2+b^2+c^2=1\)
Cmr \(\dfrac{1}{a^2+b^2}+\dfrac{1}{b^2+c^2}+\dfrac{1}{c^2+a^2}\le\dfrac{a^3+b^3+c^3}{2abc}+3\)
Lời giải:
Vì $1=a^2+b^2+c^2$ nên:
\(\frac{1}{a^2+b^2}+\frac{1}{b^2+c^2}+\frac{1}{c^2+a^2}=\frac{a^2+b^2+c^2}{a^2+b^2}+\frac{a^2+b^2+c^2}{b^2+c^2}+\frac{a^2+b^2+c^2}{c^2+a^2}\)
\(=3+\frac{a^2}{b^2+c^2}+\frac{b^2}{c^2+a^2}+\frac{c^2}{a^2+b^2}\)
\(\leq 3+\frac{a^2}{2bc}+\frac{b^2}{2ac}+\frac{c^2}{2ab}\) (theo BĐT AM-GM)
\(=3+\frac{a^3+b^3+c^3}{2abc}\) (đpcm)
Dấu "=" xảy ra khi \(a=b=c=\sqrt{\frac{1}{3}}\)
Đúng 0
Bình luận (0)
cho a,b,c>0 và \(a^2+b^2+c^2=1\) cmr
\(\dfrac{1}{a^2+b^2}+\dfrac{1}{b^2+c^2}+\dfrac{1}{c^2+a^2}\le\dfrac{a^3+b^3+c^3}{2abc}+3\)
Ta có : \(\dfrac{1}{a^2+b^2}+\dfrac{1}{b^2+c^2}+\dfrac{1}{c^2+a^2}\le\dfrac{a^3+b^3+c^3}{2abc}+3\)
\(\Leftrightarrow\dfrac{a^2+b^2+c^2}{a^2+b^2}+\dfrac{a^2+b^2+c^2}{b^2+c^2}+\dfrac{a^2+b^2+c^2}{c^2+a^2}\le\dfrac{a^3}{2abc}+\dfrac{b^3}{2abc}+\dfrac{b^3}{2abc}+3\)( vì \(a^2+b^2+c^2=1\) )
\(\Leftrightarrow3+\dfrac{a^2}{b^2+c^2}+\dfrac{b^2}{c^2+a^2}+\dfrac{c^2}{a^2+b^2}\le\dfrac{a^2}{2bc}+\dfrac{b^2}{2ca}+\dfrac{c^2}{2ab}+3\)
\(\Leftrightarrow\dfrac{a^2}{b^2+c^2}+\dfrac{b^2}{c^2+a^2}+\dfrac{c^2}{a^2+b^2}\le\dfrac{a^2}{2bc}+\dfrac{b^2}{2ac}+\dfrac{c^2}{2ab}\)
Mà theo bất đẳng thức cô-si , ta có : \(b^2+c^2\ge2bc\)\(\Rightarrow\dfrac{a^2}{b^2+c^2}\le\dfrac{a^2}{2bc}\)
Tương tự ta cũng có : \(\dfrac{b^2}{c^2+a^2}\le\dfrac{b^2}{2ca},\dfrac{c^2}{a^2+b^2}\le\dfrac{c^2}{2ab}\)
Cộng các bất đẳng thức trên lại với nhau ta được :
\(\Leftrightarrow\dfrac{a^2}{b^2+c^2}+\dfrac{b^2}{c^2+a^2}+\dfrac{c^2}{a^2+b^2}\le\dfrac{a^2}{2bc}+\dfrac{b^2}{2ac}+\dfrac{c^2}{2ab}\)
Do đó bất đẳng thức ban đầu được chứng minh .
Đúng 0
Bình luận (0)
1) Cho a, b, c ∈ [0;1] và a + b + c = 2. CMR ab + bc + ca ≥ 2abc + \(\dfrac{20}{27}\)
2) Cho a, b, c ∈ [1;3] và a + b + c = 6. CMR a3 + b3 + c3 ≤ 36
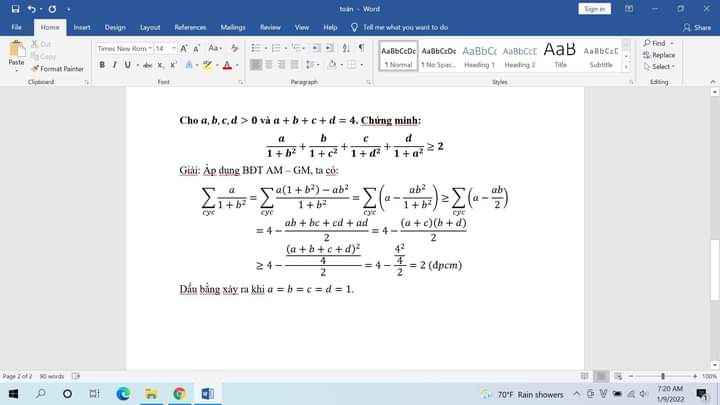
3) Cho các số dương a, b, c, d thoả mãn a + b + c + d = 4. CMR \(\dfrac{a}{1+b^2}+\dfrac{b}{1+c^2}+\dfrac{c}{1+d^2}+\dfrac{d}{1+a^2}\) ≥ 2
1.
Theo nguyên lý Dirichlet, trong 3 số a;b;c luôn có 2 số cùng phía so với \(\dfrac{2}{3}\), không mất tính tổng quát, giả sử đó là b và c
\(\Rightarrow\left(b-\dfrac{2}{3}\right)\left(c-\dfrac{2}{3}\right)\ge0\)
Mặt khác \(0\le a\le1\Rightarrow1-a\ge0\)
\(\Rightarrow\left(b-\dfrac{2}{3}\right)\left(c-\dfrac{2}{3}\right)\left(1-a\right)\ge0\)
\(\Leftrightarrow-abc\ge\dfrac{4a}{9}+\dfrac{2b}{3}+\dfrac{2c}{3}-\dfrac{2ab}{3}-\dfrac{2ac}{3}-bc-\dfrac{4}{9}\)
\(\Leftrightarrow-abc\ge-\dfrac{2a}{9}+\dfrac{2}{3}\left(a+b+c\right)-\dfrac{2ab}{3}-\dfrac{2ac}{3}-bc-\dfrac{4}{9}=-\dfrac{2a}{9}-\dfrac{2ab}{3}-\dfrac{2ac}{3}-bc+\dfrac{8}{9}\)
\(\Leftrightarrow-2abc\ge-\dfrac{4a}{9}-\dfrac{4ab}{3}-\dfrac{4ac}{3}-2bc+\dfrac{16}{9}\)
\(\Leftrightarrow ab+bc+ca-2abc\ge-\dfrac{4a}{9}-\dfrac{ab}{3}-\dfrac{ac}{3}-bc+\dfrac{16}{9}\)
\(\Leftrightarrow ab+bc+ca-2abc\ge-\dfrac{4a}{9}-\dfrac{a}{3}\left(b+c\right)-bc+\dfrac{16}{9}\ge-\dfrac{4a}{9}-\dfrac{a}{3}\left(2-a\right)-\dfrac{\left(b+c\right)^2}{4}+\dfrac{16}{9}\)
\(\Rightarrow ab+bc+ca-2abc\ge-\dfrac{4a}{9}+\dfrac{a^2}{3}-\dfrac{2a}{3}-\dfrac{\left(2-a\right)^2}{4}+\dfrac{16}{9}\)
\(\Rightarrow ab+bc+ca-2abc\ge\dfrac{a^2}{12}-\dfrac{a}{9}+\dfrac{7}{9}=\dfrac{1}{12}\left(a-\dfrac{2}{3}\right)^2+\dfrac{20}{27}\ge\dfrac{20}{27}\)
\(\Rightarrow ab+bc+ca\ge2abc+\dfrac{20}{27}\)
Dấu "=" xảy ra khi \(a=b=c=\dfrac{2}{3}\)
Đúng 1
Bình luận (1)
2.
Đặt \(\left(a;b;c\right)=\left(x+1;y+1;z+1\right)\Rightarrow\left\{{}\begin{matrix}x;y;z\in\left[0;2\right]\\x+y+z=3\end{matrix}\right.\)
Ta có: \(P=\left(x+1\right)^3+\left(y+1\right)^3+\left(z+1\right)^3\)
\(P=x^3+y^3+z^3+3\left(x^2+y^2+z^2\right)+12\)
Không mất tính tổng quát, giả sử \(x\ge y\ge z\Rightarrow x\ge1\)
\(\Rightarrow\left\{{}\begin{matrix}y^3+z^3=\left(y+z\right)^3-3yz\left(y+z\right)\le\left(y+z\right)^3\\y^2+z^2=\left(y+z\right)^2-2yz\le\left(y+z\right)^2\end{matrix}\right.\)
\(\Rightarrow P\le x^3+\left(3-x\right)^3+3x^2+3\left(3-x\right)^2+12\)
\(\Rightarrow P\le15x^2-45x+66=15\left(x-1\right)\left(x-2\right)+36\le36\)
(Do \(1\le x\le2\Rightarrow\left(x-1\right)\left(x-2\right)\le0\))
Dấu "=" xảy ra khi \(\left(x;y;z\right)=\left(2;1;0\right)\) và các hoán vị hay \(\left(a;b;c\right)=\left(1;2;3\right)\) và các hoán vị
Đúng 1
Bình luận (0)
Cho a, b, c > 0. Chứng minh: \(a^2+b^2+c^2+2abc+3\ge\left(a+1\right)\left(b+1\right)\left(c+1\right)\)