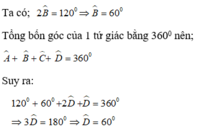D ^ = 50 0 ,    C ^ = 100 0  

Ta có : \(\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}=120+90+\widehat{C}+\widehat{D}=360^o\)

\(\Rightarrow\widehat{C}+\widehat{D}=150^o\)

Mà \(\widehat{C}=2\widehat{D}\)

\(\Rightarrow\left\{{}\begin{matrix}\widehat{C}=100\\\widehat{D}=50\end{matrix}\right.\)

Vậy ...

Ta có:

\(A+B+C+D=360^0\)

\(\Leftrightarrow120^0+90^0+2D+D=360^0\)

\(\Leftrightarrow3D=150^0\)

\(\Rightarrow D=50^0\)

\(C=2D=100^0\)

xét tứ giác ABCD ,ta có:

\(\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}=360^o\)(định lí tổng 4 góc trong tứ giác)\(\Leftrightarrow12^0+90^o+\widehat{C}+\widehat{D}=360^o\Leftrightarrow\widehat{C}+\widehat{D}=150^o\)

vì \(\widehat{C}=2\widehat{D}\) nên \(3\widehat{D}=150^o\) suy ra \(\widehat{D}=50^o,\widehat{C}=100^o\)

Ta có: ∠A + ∠B + ∠C + ∠D = 360^o

⇒ 120o + 90o + ∠C + ∠D = 360^o

⇒ ∠C + ∠D = 150^o

Lại có: ∠C = 2∠D

⇒ 2∠D + ∠D = 150^o

⇒ 3∠D = 150^o

⇒ ∠D = 50^o

∠C = ∠D.2 = 50^o/2 = 100^o

∠D = 100^o/2 = 50^o

Chọn D

a) Xét tứ giác ABCD ta có ( ^B = 2^C mới được nhé)

^A + ^B + ^C + ^D = 360⁰

=> 150⁰ + ^B + ^C + ^D = 360⁰

=> ^B + ^C + ^D = 210⁰

Có ^B = 2^C 

=> 2 ^C + ^C + ^D = 210⁰

=> 3^C + ^D = 210⁰

Có ^C = 2^D

=> 3 . 2^D + ^D = 210⁰

=> 7^D = 210⁰

=> ^D = 30⁰

+) ^C = 2^D = 2.30⁰ = 60⁰

+) ^B = 2^C = 2.60⁰ = 120⁰

b) Xét tứ giác ABCD có :

^A + ^B + (^C + ^D) = 360⁰

=> 2^B + ^B + 210⁰ = 360⁰

=> 3^B = 150⁰

=> ^B = 50⁰

+) ^A = 2^B = 2.50⁰ = 100⁰

Có ^C + ^D = 210⁰ => ^C = ^D = 210 : 2 = 105⁰

Vậy ^A = 100⁰,^B = 50⁰,^C = ^D = 105⁰

c) Áp dụng tính chất dãy tỉ số bằng nhau ta có :

\(\frac{\widehat{A}}{1}=\frac{\widehat{B}}{2}=\frac{\widehat{C}}{3}=\frac{\widehat{D}}{4}=\frac{\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}}{1+2+3+4}=\frac{360^0}{10}=36^0\)

=> ^A = 36⁰ , ^B = 72⁰ , ^C = 108⁰ , ^D = 144⁰

d) Tự làm

Xét tứ giác \(ABCD\)có : 

\(\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}=360^o\)

Mà \(\widehat{A}=36^o;\widehat{B}=48^o\)

\(\Rightarrow\widehat{C}+\widehat{D}=360^o-36^o-48^0=276^o\)

Lại có : \(\widehat{C}=2\widehat{D}\)

\(\Rightarrow2\widehat{D}+\widehat{D}=276^o\)

\(\Rightarrow3\widehat{D}=276^o\)

\(\Rightarrow\widehat{D}=92^o\)

Nên : \(\widehat{C}=92^o.2=184^o\)

Vậy \(\widehat{C}=184^o;\widehat{D}=92^o\)

Tứ giác ABCD có : \(\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}=360^o\)

mà \(36^o+48^o+\widehat{C}+\widehat{D}=360^o\)

=> \(84^o+\widehat{C}+\widehat{D}=360^o=>\widehat{C}+\widehat{D}=360^o-84^o=276^o\)

Tổng số phần bằng nhau là : 2 + 1 = 3 phần

 \(\widehat{D}=276^o:3=92^o\)

\(\widehat{C}=276^o-92^o=184^o\)

Vậy ...

Xét tứ giác ABCD có \(\widehat{A}=36^o;\widehat{B}=48^o\)

\(\Rightarrow\widehat{C}+\widehat{D}=360^O-\widehat{A}-\widehat{B}\)

\(\Rightarrow\widehat{C}+\widehat{D}=360^O-36^O-48^O=276^O\)

Ta có: \(\widehat{C}=2\widehat{D}\Rightarrow\frac{\widehat{C}}{2}=\frac{\widehat{D}}{1}\)

Áp dụng t/c DTSBN ta có:

\(\frac{\widehat{C}}{2}=\frac{\widehat{D}}{1}=\frac{\widehat{C}+\widehat{D}}{2+1}=\frac{276^O}{3}=92^O\)

\(\Rightarrow\hept{\begin{cases}\frac{\widehat{C}}{2}=92^0\Rightarrow\widehat{C}=184^O\\\frac{\widehat{D}}{1}=92^O\Rightarrow\widehat{D}=92^O\end{cases}}\)

Vậy \(\widehat{C}=184^O;\widehat{D}=92^O\)

Ta co A:B:C;D = 2:3:4:5
\(\Rightarrow\)\(\dfrac{A}{2}\) = \(\dfrac{B}{3}\) = \(\dfrac{C}{4}\) = \(\dfrac{D}{5}\) = \(\dfrac{A+B+C+D}{2+3+4+5}\) = \(\dfrac{360}{14}\) = \(\dfrac{180}{7}\)
\(\Rightarrow\) A= \(\dfrac{180}{7}\). 2 \(\approx\) 51
    B= \(\dfrac{180}{7}\). 3  \(\approx\) 77
    C=  \(\dfrac{180}{7}\). 4  \(\approx\) 103
   D=  \(\dfrac{180}{7}\). 5  \(\approx\) 129
Ta thay: A+D=180 ; B+C=180 \(\Rightarrow\) ABCD la hinh thang

Gọi số đo góc D là x^o thì \(\widehat{C}=\left(x+10\right)^o;\widehat{B}=\left(x+20\right)^o;\widehat{A}=\left(x+30\right)^o\)

Do tổng các góc trong tứ giác bằng 360^o nên ta có phương trình:

x + x + 10 + x + 20 + x + 30 = 360

\(\Rightarrow x=75\)

Vậy \(\widehat{D}=75^o,\) từ đó suy ra các góc còn lại.

Em cảm ơn cô ạ!