Cho a,b,c,d>0 thoả mãn: ab=cd=1. CMR: (a+b)(c+d)+4\(\ge\) 2(a+b+c+d)

Những câu hỏi liên quan
Với a,b,c,d là các số dưong thoả mãn ab=cd=1.CMR:
(a+b)(c+d)+4\(\ge\)2(a+b+c+d)
Đặt \(\hept{1\begin{cases}a+b=x\\c+d=y\end{cases}}\)thì ra cần chứng minh
\(xy+4\ge2\left(x+y\right)\)
\(\Leftrightarrow\left(x-2\right)\left(y-2\right)\ge0\)
Mà ta có
\(\hept{\begin{cases}x=a+b\ge2\sqrt{ab}=2\\y=c+d\ge2\sqrt{cd}=2\end{cases}}\)
\(\Rightarrow\)ĐPCM
Đúng 0
Bình luận (0)
Cái m dùng là bất đẳng thức cosi kết hợp với phương pháp đặt ẩn phụ mà
Đúng 0
Bình luận (0)
$\rm Cho\ a,b,c \ge 0 .Thoả \ mãn \ ab+bc+ac=abc .Chứng \ minh\ a^{2}+b^{2}+c^{2}+5abc \ge 8$
`b)` Cho` a,b,c>=0,ab+bc+ca+abc=4`
CMR:`a^2+b^2+c^2+5abc>=8`
a. Đề bài sai (thực chất là nó đúng 1 cách hiển nhiên nhưng "dạng" thế này nó sai sai vì ko ai cho kiểu này cả)
Ta có: \(abc=ab+bc+ca\ge3\sqrt[3]{a^2b^2c^2}\Rightarrow abc\ge27\)
\(\Rightarrow a^2+b^2+c^2+5abc\ge a^2+b^2+c^2+5.27>>>>>8\)
b.
\(4=ab+bc+ca+abc=ab+bc+ca+\sqrt{ab.bc.ca}\le ab+bc+ca+\sqrt{\left(\dfrac{ab+bc+ca}{3}\right)^3}\)
\(\sqrt{\dfrac{ab+bc+ca}{3}}=t\Rightarrow t^3+3t^2-4\ge0\Rightarrow\left(t-1\right)\left(t+2\right)^2\ge0\)
\(\Rightarrow t\ge1\Rightarrow ab+bc+ca\ge3\Rightarrow a+b+c\ge\sqrt{3\left(ab+bc+ca\right)}\ge3\)
- TH1: nếu \(a+b+c\ge4\)
Ta có: \(ab+bc+ca=4-abc\le4\)
\(\Rightarrow P=\left(a+b+c\right)^2-2\left(ab+bc+ca\right)+5abc\ge4^2-2.4+0=8\)
(Dấu "=" xảy ra khi \(\left(a;b;c\right)=\left(2;2;0\right)\) và các hoán vị)
- TH2: nếu \(3\le a+b+c< 4\)
Đặt \(a+b+c=p\ge3;ab+bc+ca=q;abc=r\)
\(P=p^2-2q+5r=p^2-2q+5\left(4-q\right)=p^2-7q+20\)
Áp dụng BĐT Schur:
\(4=q+r\ge q+\dfrac{p\left(4q-p^2\right)}{9}\Leftrightarrow q\le\dfrac{p^3+36}{4p+9}\)
\(\Rightarrow P\ge p^2-\dfrac{7\left(p^3+36\right)}{4p+9}+20=\dfrac{3\left(4-p\right)\left(p-3\right)\left(p+4\right)}{4p+9}+8\ge8\)
(Dấu "=" xảy ra khi \(a=b=c=1\))
Đúng 1
Bình luận (0)
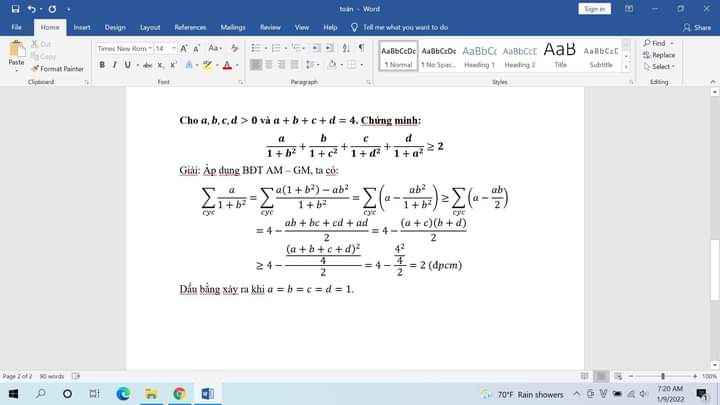
cho a,b,c,d >0 thoả mãn a+b+c+d = 4
cmr \(\frac{a}{1+b^2}\)+ \(\frac{b}{1+c^2}\)+\(\frac{c}{1+d^2}\)+ \(\frac{d}{1+a^2}\)\(\ge\)2
Ta có \(\frac{a}{1+b^2}=a-\frac{ab^2}{1+b^2}\ge a-\frac{ab^2}{2b}=a-\frac{ab}{2}\)
Tương tự \(\frac{b}{1+c^2}\ge b-\frac{bc}{2}\)
\(\frac{c}{1+d^2}\ge c-\frac{cd}{2}\)
\(\frac{d}{1+a^2}\ge d-\frac{ad}{2}\)
Lại có \(ab+bc+cd+da\le\frac{\left(a+b+c+d\right)^2}{4}=\frac{4^2}{4}=4\)
Do đó \(\frac{a}{1+b^2}+\frac{b}{1+c^2}+\frac{c}{1+d^2}+\frac{d}{1+a^2}\ge\left(a+b+c+d\right)-\frac{ab+bc+cd+da}{2}\)
\(\ge4-\frac{4}{2}=2\)
Đẳng thức xảy ra \(\Leftrightarrow\) \(a=b=c=d=1\)
Đúng 0
Bình luận (0)
1) Cho a, b, c ∈ [0;1] và a + b + c = 2. CMR ab + bc + ca ≥ 2abc + \(\dfrac{20}{27}\)
2) Cho a, b, c ∈ [1;3] và a + b + c = 6. CMR a3 + b3 + c3 ≤ 36
3) Cho các số dương a, b, c, d thoả mãn a + b + c + d = 4. CMR \(\dfrac{a}{1+b^2}+\dfrac{b}{1+c^2}+\dfrac{c}{1+d^2}+\dfrac{d}{1+a^2}\) ≥ 2
1.
Theo nguyên lý Dirichlet, trong 3 số a;b;c luôn có 2 số cùng phía so với \(\dfrac{2}{3}\), không mất tính tổng quát, giả sử đó là b và c
\(\Rightarrow\left(b-\dfrac{2}{3}\right)\left(c-\dfrac{2}{3}\right)\ge0\)
Mặt khác \(0\le a\le1\Rightarrow1-a\ge0\)
\(\Rightarrow\left(b-\dfrac{2}{3}\right)\left(c-\dfrac{2}{3}\right)\left(1-a\right)\ge0\)
\(\Leftrightarrow-abc\ge\dfrac{4a}{9}+\dfrac{2b}{3}+\dfrac{2c}{3}-\dfrac{2ab}{3}-\dfrac{2ac}{3}-bc-\dfrac{4}{9}\)
\(\Leftrightarrow-abc\ge-\dfrac{2a}{9}+\dfrac{2}{3}\left(a+b+c\right)-\dfrac{2ab}{3}-\dfrac{2ac}{3}-bc-\dfrac{4}{9}=-\dfrac{2a}{9}-\dfrac{2ab}{3}-\dfrac{2ac}{3}-bc+\dfrac{8}{9}\)
\(\Leftrightarrow-2abc\ge-\dfrac{4a}{9}-\dfrac{4ab}{3}-\dfrac{4ac}{3}-2bc+\dfrac{16}{9}\)
\(\Leftrightarrow ab+bc+ca-2abc\ge-\dfrac{4a}{9}-\dfrac{ab}{3}-\dfrac{ac}{3}-bc+\dfrac{16}{9}\)
\(\Leftrightarrow ab+bc+ca-2abc\ge-\dfrac{4a}{9}-\dfrac{a}{3}\left(b+c\right)-bc+\dfrac{16}{9}\ge-\dfrac{4a}{9}-\dfrac{a}{3}\left(2-a\right)-\dfrac{\left(b+c\right)^2}{4}+\dfrac{16}{9}\)
\(\Rightarrow ab+bc+ca-2abc\ge-\dfrac{4a}{9}+\dfrac{a^2}{3}-\dfrac{2a}{3}-\dfrac{\left(2-a\right)^2}{4}+\dfrac{16}{9}\)
\(\Rightarrow ab+bc+ca-2abc\ge\dfrac{a^2}{12}-\dfrac{a}{9}+\dfrac{7}{9}=\dfrac{1}{12}\left(a-\dfrac{2}{3}\right)^2+\dfrac{20}{27}\ge\dfrac{20}{27}\)
\(\Rightarrow ab+bc+ca\ge2abc+\dfrac{20}{27}\)
Dấu "=" xảy ra khi \(a=b=c=\dfrac{2}{3}\)
Đúng 1
Bình luận (1)
2.
Đặt \(\left(a;b;c\right)=\left(x+1;y+1;z+1\right)\Rightarrow\left\{{}\begin{matrix}x;y;z\in\left[0;2\right]\\x+y+z=3\end{matrix}\right.\)
Ta có: \(P=\left(x+1\right)^3+\left(y+1\right)^3+\left(z+1\right)^3\)
\(P=x^3+y^3+z^3+3\left(x^2+y^2+z^2\right)+12\)
Không mất tính tổng quát, giả sử \(x\ge y\ge z\Rightarrow x\ge1\)
\(\Rightarrow\left\{{}\begin{matrix}y^3+z^3=\left(y+z\right)^3-3yz\left(y+z\right)\le\left(y+z\right)^3\\y^2+z^2=\left(y+z\right)^2-2yz\le\left(y+z\right)^2\end{matrix}\right.\)
\(\Rightarrow P\le x^3+\left(3-x\right)^3+3x^2+3\left(3-x\right)^2+12\)
\(\Rightarrow P\le15x^2-45x+66=15\left(x-1\right)\left(x-2\right)+36\le36\)
(Do \(1\le x\le2\Rightarrow\left(x-1\right)\left(x-2\right)\le0\))
Dấu "=" xảy ra khi \(\left(x;y;z\right)=\left(2;1;0\right)\) và các hoán vị hay \(\left(a;b;c\right)=\left(1;2;3\right)\) và các hoán vị
Đúng 1
Bình luận (0)
Cho các số nguyên a,b,c,d khác 0 thoả mãn ab=cd.
CMR: a2014+b2014+c2014+d2014 là hợp số
bạn dựa vào bài tương tự này nha :
Cho a,b,c,d là các số nguyên dương thỏa mãn: ab=cd. Chứng minh rằng: A=anan+bnbn+cncn+dndn là hợp số với mọi số nguyên dương n.
langtuthattinh và The gunners thích#2 ![]() Nguyen Duc Thuan
Nguyen Duc Thuan
Sĩ quan
 Thành viên
Thành viênĐã gửi 06-02-2013 - 22:17
Vào lúc 06 Tháng 2 2013 - 22:04, 'hoangtubatu955' đã nói:
Cho a,b,c,d là các số nguyên dương thỏa mãn: ab=cd. Chứng minh rằng: A=anan+bnbn+cncn+dndn là hợp số với mọi số nguyên dương n.
Đặt (a;c)=q thì a=qa1;c=qc1a=qa1;c=qc1 (Vs (a1;c1a1;c1=1)
Suy ra ab=cd ⇔ba1=dc1⇔ba1=dc1
Dẫn đến d⋮a1d⋮a1 đặt d=a1d1d=a1d1 thay vào đc:
b=d1c1b=d1c1
Vậy an+bn+cn+dn=q2an1+dn1cn1+qncn1+an1dn1=(cn1+an1)(dn1+qn)an+bn+cn+dn=q2a1n+d1nc1n+qnc1n+a1nd1n=(c1n+a1n)(d1n+qn)
là hợp số (QED) 

Đúng 0
Bình luận (0)
cho 4 số thực dương a,b,c,d thỏa mãn a+b+c+d=4.CMR:
\(\frac{1}{ab}+\frac{1}{cd}\ge\frac{a^2+b^2+c^2+d^2}{2}\)
cho 4 số nguyên a,b,c,d thỏa mãn : a + b = c + d ; ab + 1 = cd . CMR : c = d
Cho các số nguyên a,b,c,d thoả mãn ab - cd = 1 và a + b= c + d. Chứng minh rằng a=b
Cho a,b,c,d thoả mãn a2 +b2+c2+d2=2019 và ad+bc=0.tính giá trị của A=ab+cd