I : Cho tứ giác ABCD , M N là trung điểm của AD và BC , I là trung điểm của AC
a) C/m : MI//CD
b) Biết MN=AB+CD/2 . C/m ABCD là hình thang
1. Cho tứ giác ABCD. Gọi M,N là trung điểm của AD và BC. Biết MN=(AB+CD):2. C/M ABCD là hình thang
Cho tứ giác ABCD. Gọi M, N là trung điểm của AD và BC, biết MN =(AB + CD)/2. C/M ABCD là hình thang
gọi I là giao điểm của MN và BD
ta có
MN=(AB + DC)/2
=> MI + IN = AB/2 + DC/2
=> MI = AB/2 và IN = DC/2
=> MI và IN là đường tb của tam giác ABD và tam giác BDC
=> MI // AB và IN // DC
vì M,I,N thẳng hàng nên => AB // DC => tứ giác ABCD là hình thang
. Cho hình thang cân ABCD đáy AB < CD. Gọi M, N lần lượt là trung điểm của AD và BC, MN giao BD tại I. Biết AD = 10cm, MI = 6cm, NI = 12cm. Tính diện tích tứ giác ABCD
Bài 1: Tứ giác ABCD có AB=BC=CD và Góc D+B=180 độ
a, Chứng minh AC là phân giác góc A
b, Tứ giác ABCD là hình gì? tại sao?
Bài 2: Cho hình thang ABCD (AB//CD). M là trung điểm của AD sao cho CM là phân giác góc C. Biết MB=6cm, MC=8cm
a, BC=?
b, So sánh khoảng cách từ M đến BC và đường cao hình thang.
Bài 3: Cho tứ giác ABCD, AC là phân giác góc A. Gọi I,K lần lượt là trung điểm của AD,BC. IK cắt AC tại S.
a, Cmr: S là trung điểm của AC
b, Từ C kẻ Cx//AD. Cx cắt AB tại M. Tứ giác ABCD là hình gì? tại sao?
Bài 4: Cho tứ giác ABCD gọi E,F lần lượt là trung điểm của BC và AD.
Cmr:
a,EF<(AB+CD)/2
b, Tứ giác ABCD<=>EF<(AB+CD)/2
Bài 5: Cho hình thang ABCD (AB//CD), AB<CD. AC cắt BD tại O. Biết gócDOC=60 độ
AD=6cm. P,Q,R lần lượt là trung điểm của OA,OD. Tính chu vi tam giác PQR
Bài 6: Cho tam giác ABC, D thuộc AB sao cho BD=1/4 AB, E là trung điểm vủa BC. Đường thẳng DE cắt AC tại F. Cmr: CF=1/2AC.
Các bạn xem làm giúp mình với nhé mình sắp phải nộp rồi
Bài 1:
a: Xét tứ giác ABCD có góc B+góc D=180 độ
nên ABCD là tứ giác nội tiếp
=>góc BAC=góc BDC và góc DAC=góc DBC
mà góc CBD=góc CDB
nên góc BAC=góc DAC
hay AC là phân giác của góc BAD
b: Ta có: góc BCA=góc BAC
=>góc BCA=góc CAD
=>BC//AD
=>ABCD là hình thang
mà góc B=góc BCD
nên ABCD là hình thang cân
Bài 1 cho tứ giác ABCD, P,Q lần lượt là trung điểm của AD và BC,a chứng minh PQ hoặc AB AC 2,b tứ giác ABCD là hình thang PQ AB CD 2. Bài 2 cho hình thang ABCD, AB đáy lớn. M ,N,P,Q lần lượt là trung điểm của AD BC AC BD.a chứng Minh M N P Q thẳng hàng.b Cho AB a CD b với a b. Tính MN PQ.c Cm rằng nếu MP PQ QN thì a 2b
cho hình thang ABCD (AB//CD)
a/ gọi M,N,P,Q lần lượt là trung điểm của AD ,BC,BD,AC .Chứng minh M,N,P,Q thẳng hàng .Tính MN ,PQ biết AB =a ,CD =b(a<b)
b/gọi I,J là trung điểm của AB,CD .Tứ giác IPJQ là hình gì
c/gọi A*B*C*D* lần lượt là trung điểm của AN ,BM,CM,DN.Chứng minh rằng A*B*C*D* là hình bình hành
Cho hình thang ABCD (AB // CD), M là trung điểm của AD, N là trung điểm của BC. Gọi I, K theo thứ tự là giao điểm của MN với BD, AC. Cho biết AB = 6cm, CD = l4cm. Tính độ dài MI, IK, KN.
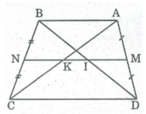
Hình thang ABCD có AB // CD
M là trung điểm của AD (gt)
N là trung điểm của BC (gt)
Nên MN là đường trung bình của hình thang ABCD ⇒ MN//AB// CD
MN = (AB + CD) / 2 = (6 + 14) / 2 = 10 (cm)
* Trong tam giác ADC, ta có:
M là trung điểm của AD
MK // CD
⇒ AK= KC và MK là đường trung bình của ∆ ADC.
⇒ MK = 1/2 CD = 1/2 .14= 7 (cm)
Vậy: KN = MN – MK = 10 – 7 = 3 (cm)
* Trong ∆ ADB, ta có:
M là trung điểm của AD
MI // AB nên DI = IB
⇒ MI là đường trung bình của ∆ DAB
⇒ MI = 1/2 AB = 1/2 .6 = 3 (cm)
IK = MK – Ml = 7 – 3 = 4 (cm)
Cho tứ giác ABCD. Gọi M,I,N là trung điểm AB,AC và CD. CMR nếu MN=AD+BC/2 thì M,I và N thẳng hằng và ABCD là hình thang
GE≤GM+ME=12CD+12AB=AB+CD2GE≤GM+ME=12CD+12AB=AB+CD2
Dấu "=" xảy ra ⇔⇔ Ba điểm M, G, E thẳng hàng.
⇔⇔ GE // AB và GE // CD ⇔⇔ AB // CD
⇔⇔ Tứ giác ABCD là hình thang.
Cho hình thang ABCD (AB // CD). Gọi O là giao điểm của AC và BD. I là giao điểm của AD và BC. Gọi M, N lần lượt là trung điểm của AB và CD. a) Chứng minh rằng I, M, O, N thẳng hàng b) Giả sử CD=3AB và diện tích hình thang ABCD bằng a, Hãy tính diện tích tứ giác IAOB theo a
Cho tứ giác ABCD (AB không song song với CD). Giả sử M, N lần lượt là đường trung bình của AB và CD, thỏa mãn: MN = BC + AD / 2 . Gọi I là trung điểm của BD. Chứng minh: ABCD là hình thang.