Cho a,b là các số hữu tỉ;p là số nguyên tố thoả mãn a+b\(\sqrt{p}\)=0.Chứng minh rằng a=b=0.
KẾT BẠN NHA CÁC BẠN!
Cho các số thực a,b,c thỏa mãn a + b, b + c, c + a đều là các số hữu tỉ. Chứng minh rằng a, b, c là các số hữu tỉ
a + b, b + c, c + a đều là các số hữu tỉ
=> 2(a + b + c) là số hữu tỉ
=> a + b + c là số hữu tỉ (do khi 1 số hữu tỉ chia cho 2 sẽ nhận đc 1 số hữu tỉ)
=> a + b + c - (a + b) = c là số hữu tỉ; a + b + c - (b + c) = a là số hữu tỉ; a + b + c - (c + a) = b là số hữu tỉ
=> a, b, c đều là số hữu tỉ (đpcm)
Cho các thực a,b thoả mãn 2a+3b và 5a-4b đều là các số hữu tỉ. Chứng minh rằng a,b đều là các số hữu tỉ
Ta có: 2a+3b là số hữu tỉ
=> 5(2a+3b)=10a+15b là số hữu tỉ
5a-4b là số hữu tỉ
=> 2(5a-4b)=10a -8b là số hữu tỉ
=> (10a+15b)-(10a-8b)=10a+15b-10a+8b=23b
=> b là số hữu tỉ
=> 3b là số hữu tỉ
=> (2a+3b)-3b =2a là số hữu tỉ
=> a là số hữu tỉ
cho a,b,c là các số hữu tỉ không âm và thỏa mãn \(\sqrt{a}+\sqrt{b}+\sqrt{c}\) là số hữu tỉ. Chứng minh \(\sqrt{a},\sqrt{b},\sqrt{c}\)là các số hữu tỉ
Cho a,b là các số hữu tỉ thỏa mãn \(a^3+b^3\)=4ab. Cmr 4-ab là bình phương của một số hữu tỉ
\(a^3+b^3=4ab\)
\(\Rightarrow a^3=4ab-b^3\)
\(\Rightarrow a=\dfrac{4ab-b^3}{a^2}\)
\(4-ab=4-\dfrac{4ab-b^3}{a^2}.b=4-\dfrac{4ab^2-b^4}{a^2}=\dfrac{4a^2-4ab^2+b^4}{a^2}=\dfrac{\left(2a-b^2\right)^2}{a^2}=\left(\dfrac{2a-b^2}{a}\right)^2\)
xét xem các số a và b có thể là số vô tỉ hay khồn nếu :
a, ab và a/b là các số hữu tỉ
b, a+b và a/b là các số hữu tỉ ( a+b#0)
c, a+b , a^2 và b^2 là các số hữu tỉ ( a+b#0)
1. Cho các số hữu tỉ .
a/ Hãy so sánh các số hữu tỉ đó .
b/ Viết tập hợp các số hữu tỉ bằng các số hữu tỉ trên .
Xét xem các số a,b là các số vô tỉ hay không nếu: a) a.b là số hữu tỉ b) a+b và a/b là số hữu tỉ c) a.b, \(a^2\),\(b^2\)là số hữu tỉ
a/ Có thể là vô tỉ. Ví dụ: \(\hept{\begin{cases}a=\sqrt{2}\\b=\sqrt{2}\end{cases}}\)
b/ Không thể vì
Giả sử a, b là số vô tỷ
Nếu \(\frac{a}{b}\)là số hữu tỷ thì có dạng
\(\hept{\begin{cases}a=m.q\\b=n.q\end{cases}\left(m,n\in Q;q\in I\right)}\)
\(\Rightarrow a+b=m.q+n.q=q\left(m+n\right)\in I\)
Trái giả thuyết.
c/ Có thể Ví dụ: \(\hept{\begin{cases}a=\sqrt{2}\\b=\sqrt{2}\end{cases}}\)
Trong các câu sau câu nào đúng câu nào sai”
a. Số hữu tỉ âm nhỏ hơn số hữu tỉ dương
b. Số hữu tỉ âm nhỏ hơn số tự nhiên
c. Số 0 là số hữu tỉ dương
d. Số nguyên âm không phải là số hữu tỉ âm
e. Tập hợp Q gồm các số hữu tỉ dương và các số hữu tỉ âm
a. Số hữu tỉ âm nhỏ hơn số hữu tỉ dương. Đúng
b. Số hữu tỉ âm nhỏ hơn số tự nhiên. Đúng
c. Số 0 là số hữu tỉ dương. Sai
Vì số 0 không là số hữu tỉ dương cũng không là số hữu tỉ âm.
d. Số nguyên âm không phải là số hữu tỉ âm. Sai
Các số nguyên âm a luôn viết được dưới dạng: 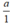 . Do đó, số nguyên âm có là số hữu tỉ âm.
. Do đó, số nguyên âm có là số hữu tỉ âm.
e. Tập hợp Q gồm các số hữu tỉ dương và các số hữu tỉ âm. Sai
Vì tập hợp Q gồm các số hữu tỉ dương, các số hữu tỉ âm và số 0.
Xét xem các số a và b có thể là số vô tỉ hay không, nếu :
a, a + b và a - b là các số hữu tỉ
b, a - b và b là các số hữu tỉ
xin lỗi nhưng mk mới lớp 6 không thể giúp rồi
Câu 2. Trong các câu sau, câu nào đúng?
A. Số hữu tỉ âm nhỏ hơn số hữu tỉ dương.
B. Số 0 là số hữu tỉ dương.
C. Số nguyên âm không phải là số hữu tỉ âm.
D. Tập hợp gồm các số hữu tỉ dương và các số hữu tỉ âm.
Giai thich :)))
`#3107.101107`
2.
A. Số hữu tỉ âm nhỏ hơn số hữu tỉ dương - Đúng
Vì số hữu tỉ âm nằm bên trái của trục số thực và bé hơn 0
B. Số 0 là số hữu tỉ dương - Sai
Số 0 không phải là số hữu tỉ dương cũng không phải là số hữu tỉ âm
C. Số nguyên âm không phải số hữu tỉ âm - Sai
Các số nguyên âm x có thể được viết dưới dạng `x/1`, do đó số nguyên âm cũng là số hữu tỉ âm
D. Tập hợp Q gồm các số hữu tỉ dương và các số hữu tỉ âm? - Sai
Tập hợp Q bao gồm các số hữu tỉ âm, dương và cả số 0.
`=>` Chọn đáp án A.