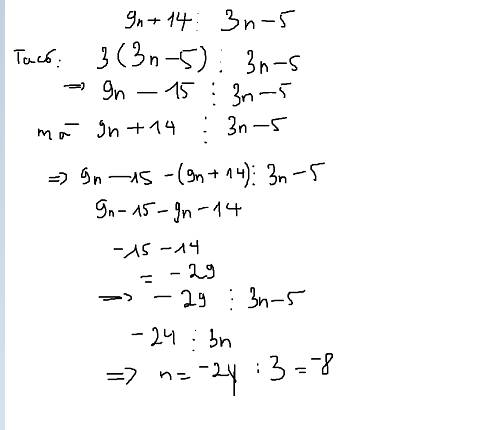9n + 21 chia hết 3n + 2

Những câu hỏi liên quan
Bài1: Tìm chũ số a, b biết :
a, 21a49b chia hết cho 99
b, a-b =2 và 48a597b chia hết cho 99
c, 2a-b=3 và 697a5134b chia hết cho 9
Bài 2: tìm n là số tự nhiên
a, 2n2+14 chia hết cho n+1
b, 3n2+9n +21 chia hết cho 3n+1
c, 4n+15 chia hết cho 3n-1
d, 3n +10 chia hết cho 2n+1
a; 10n2+9n+3chia hết cho2n+5
b; 4-9n-7n2chia hết cho 3n+5
a: \(\Leftrightarrow10n^2+25n-16n-40+43⋮2n+5\)
\(\Leftrightarrow2n+5\in\left\{1;-1;43;-43\right\}\)
hay \(n\in\left\{-2;-3;19;-24\right\}\)
b: \(\Leftrightarrow7n^2+9n-4⋮3n+5\)
\(\Leftrightarrow21n^2+27n-12⋮3n+5\)
\(\Leftrightarrow21n^2+35n-8n-\dfrac{40}{3}+\dfrac{4}{3}⋮3n+5\)
\(\Leftrightarrow3n+5\in\left\{1;-1;2;-2;4;-4\right\}\)
hay \(n\in\left\{-2;-1;-3\right\}\)
Đúng 0
Bình luận (0)
CMR: 9n3 +9n2 +3n -16 không chia hết cho 343 Với mọi n thuộc N
ta có 343=7^3
vì 9n^3 không chia hết cho 7
vì 9n^2 không chia hết cho 7
vì 3n không chia hết cho 7
vì 16 không chia hết cho 7
=> 9n^3+9n^2+3n-16 không chia hết cho 343
Đúng 0
Bình luận (0)
2) Tìm các số nguyên n để 9n + 14 chia hết cho 3n - 5
cíuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuu
Đúng 1
Bình luận (0)
2) Tìm các số nguyên n để 9n + 14 chia hết cho 3n - 5
cíuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuu
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
1. A = 1+2+2^2+....+2^21 cho 7
2. Chứng minh rằng:
A= 1-3+3^2+...+3^99 chia hết cho 4
3. CMR: 9n+24 và 3n+7 là 2 số nguyên tố cùng nhau.
4. Tìm các số nguyên x,y biết:
ab+3a-2b+6=6
Xem chi tiết
Trả lời cho mình nhanh nhé. Ngày mai mình phải nộp rồi.
Giúp mình nhanh nhé

Tìm số tự nhiên n để ( 9n + 15 ) chia hết cho ( 3n - 2 )
Chứng minh rằng với mọi n là stn ta có :
1. n2-5n chia hết cho 2
2. 3n2+9n chia hết cho 6
a) 3n2 - 4n + 5 chia hết cho n - 1
b) n2 - 7n + 2 chia hết cho n - 2
c) n2 + 9n + 6 chia hết cho n - 3
a) 3n + 2 chia hết cho n - 1
⇒⇒ 3n - 3 + 5 chia hết cho n - 1
⇒⇒ 3(n - 1) + 5 chia hết cho n - 1
⇒⇒ 5 chia hết cho n - 1
⇒⇒ n - 1 ∈∈ Ư(5) = {-1; 1; -5; 5}
⇒⇒ n ∈∈ {0; 2; -4; 6}
b) 3n + 24 chia hết cho n - 4
⇒⇒ 3n - 12 + 36 chia hết cho n - 4
⇒⇒ 3(n - 4) + 36 chia hết cho n - 4
⇒⇒ 36 chia hết cho n - 4
⇒⇒ n - 4 ∈∈ Ư(36) = {-1; 1; -2; 2; -3; 3; -4; 4; -6; 6; -9; 9; -12; 12; -18; 18; -36; 36}
⇒⇒ n ∈∈ {-3; 5; 4; 6; -1; 7; 0; 8; -2; 10; -5; 13; -8; 16; -14; 22; -32; 40}
c) 3n + 5 chia hết cho n + 1
⇒⇒ 3n + 3 + 2 chia hết cho n + 1
⇒⇒ 3(n + 1) + 2 chia hết cho n + 1
⇒⇒ 2 chia hết cho n + 1
⇒⇒ n + 1 ∈∈ Ư(2) = {-1; 1; -2; 2}
⇒⇒ n ∈∈ {0; 2; -1; 3}