Bài làm

Xét tam giác AEB và tam giác DFB có:

\(\widehat{BEA}=\widehat{BFD}=90^0\)

Cạnh huyền AB = BD ( Do ABCD là hình thoi nên AB = AC = CD = BD )

Góc nhọn: \(\widehat{A}=\widehat{D}\)( hai góc đối của hình thoi )

=> Tam giác AEB = tam giác DFB ( cạnh huyền - góc nhọn )

=> BE = BF ( hai cạnh tương ứng )

=> Tam giác BEF cân tại B.

Xét tam giác ABE vuông tại E có:

\(\widehat{A}+\widehat{ABE}=90^0\)( hai góc phụ nhau )

hay \(60^0+\widehat{ABE}=90^0\)

=> \(\widehat{ABE}=90^0-60^0=30^0\)

Mà \(\widehat{ABE}=\widehat{DBF}=30^0\)( Vì tam giác AEB = tam giác DFB )

Ta có: \(\widehat{ABD}+\widehat{BDC}=180^0\)( Do BA // DC và hai góc này là hai góc trong cùng phía bù nhau )

=> \(\widehat{ABE}+\widehat{EBF}+\widehat{FBD}+\widehat{BDC}=180^0\)

hay \(30^0+\widehat{EBF}+30^0+60^0=180^0\)

=> \(\widehat{EBF}=180^0-60^0-30^0-30^0\)

=> \(\widehat{EBF}=60^0\)

Mà tam giác EBF cân tại B ( chứng minh trên )

=> Tam giác EBF là tam giác đều. 

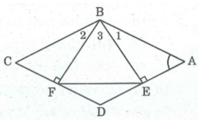
Xét hai tam giác vuông BEA và BFC, ta có:

∠ (BEA) =  ∠ (BFC) = 90 0

∠ A =  ∠ C (tính chất hình thoi)

BA = BC (gt)

Suy ra: ∆ BEA =  ∆ BFC (cạnh huyền, góc nhọn)

Do đó, ta có:

* BE = BF ⇒ ΔBEF cân tại B

*  ∠ B 1  =  ∠ B 2

Trong tam giác vuông BEA, ta có:

∠ A +  ∠ B1=  90 0  ⇒  ∠ B1=  90 0  –  ∠ A =  90 0 - 60 0 = 30 0

⇒  ∠ B 2 =  ∠ B 1  =  30 0

∠ A +  ∠ (ABC) =  180 0  (hai góc trong cùng phía bù nhau)

⇒  ∠ (ABC) =  180 0  –  ∠ A =  180 0 - 60 0 = 120 0

⇒  ∠ (ABC) =  ∠ B 1 +  ∠ B 2 +  ∠ B 3

⇒ ∠ B 3  =  ∠ (ABC) – ( ∠ B 1  +  ∠ B 2 ) =  120 0 - 30 0 + 30 0 = 60 0

Tam giác BEF cân tại B có  ∠ (EBF) =  60 0  nên ∆ BEF đều.