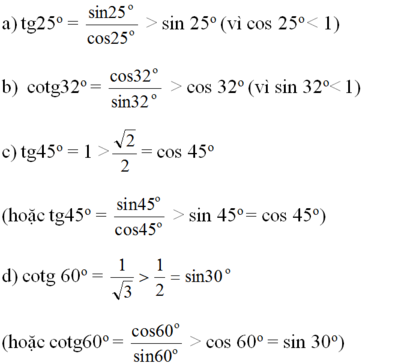so sánh sin47 và cos32

Những câu hỏi liên quan
So sánh:
a
)
t
g
25
°
v
à
sin
25
°
;
b
)
c
o
t
g
32
°
v
à
cos
32
°
c
)
t
g
45
°
v
à
co...
Đọc tiếp
So sánh:
a ) t g 25 ° v à sin 25 ° ; b ) c o t g 32 ° v à cos 32 ° c ) t g 45 ° v à cos 45 ° ; d ) c o t g 60 ° v à sin 30 °
So sánh:
a. \(\tan25°\) và \(\sin25°\)
b. \(\cot32°\) và \(\cos32°\)
c. \(\tan45°\) và \(\cos45°\)
d. \(\cot60°\) và \(\sin30°\)
Lời giải:
a. $\tan 25^0=\frac{\sin 25^0}{\cos 25^0}> \sin 25^0$ do $0< \cos 25^0< 1$
b. $\cot 32^0 = \frac{\cos 32^0}{\sin 32^0}> \cos 32^0$ do $0< \sin 32^0< 1$
c. $\tan 45^0= 1; \cos 45^0=\frac{\sqrt{2}}{2}$ nên $\tan 45^0> \cos 45^0$
d. $\cot 60^0= \frac{\cos 60^0}{\sin 60^0}=\frac{\sin 30^0}{\sin 60^0}> \sin 30^0$ do $0< \sin 60^0< 1$
Đúng 1
Bình luận (0)
So sánh :
a) \(tg25^0\) và \(\sin25^0\)
b) \(cotg32^0\) và \(\cos32^0\)
c) \(tg45^0\) và \(\cos45^0\)
d) \(cotg60^0\) và \(\sin30^0\)
Dùng tính chất và .
ĐS:
a) ;
b) ;
c) ;
d) .
Đúng 0
Bình luận (0)
So sánh:
a) tg250 và sin250
b)cotg320 và cos320;
c) tg450 và cos450;
d) cotg600 và sin300.
Đừng ghi dấu không thôi , các bạn giải rõ giúp mình với nhé ( ví dụ là: Vì sao tg250 > sin250 )
So sánh:a) tg250 và sin250b)cotg320 và cos320;c) tg450 và cos450;d) cotg600 và sin300.Bài a) cô giáo mình giải như thế này này:tg250 frac{sin25}{cos25} cos 25 1 tg250 sin250 Vì sao lại tg250 frac{sin25}{cos25} giải thích giúp mình với, cảm ơn!
Đọc tiếp
So sánh:
a) tg250 và sin250
b)cotg320 và cos320;
c) tg450 và cos450;
d) cotg600 và sin300.
Bài a) cô giáo mình giải như thế này này:
tg250 =\(\frac{\sin25}{cos25}\) cos 25 < 1
=> tg250 > sin250
Vì sao lại tg250 =\(\frac{\sin25}{cos25}\) giải thích giúp mình với, cảm ơn!
a) ta có tan 25 =sin25 phần cos25 và sin25=sin25 phần 1 suy ra sin25 phần cos25> sin25 phần 1 (vì cos25 <1) vậy tan25>sin25( điều 1)
b) ta có cot32= cos32 phần sin32 và cos32= sos32 phần 1 suy ra cos32 phần sin32>cos32 phần 1(vì sin32<1) vậy cot32>cos32
c) ta có tan45=sin45 phần cos45 và cos45= cos45= cos45 phần 1 suy ra sin45 phần cos45> cos45 phần 1(vì cos45<1) vậy tan45>cos45
d) ta có cot60=cos60 phần sin60 và sin30 =cos60 phần 1 suy ra cos60 phần sin60> cos60 phần 1 (vì sin60 <1) vậy cot60>sin30
Đúng 0
Bình luận (0)
trong bài 14 (sgk -77) có yêu cầu chứng minh tan = sin phần cos đó bạn
Đúng 0
Bình luận (0)
Đẳng thức nào sau đây là đúng: *
a. sin50 độ = cot40 độ
b. tan40 độ = cot60 độ
c. cot50 độ = tan45 độ
d. sin58 độ = cos32 độ
\(sin58^0=cos32^0\)
Đáp án D đúng
Đúng 0
Bình luận (0)
Xếp theo thứ tự từ nhỏ đến lớn: \(\sin78^o;\cos14^o;\sin47^o;\cos87^o\)
Ta có: \(cos14^o=sin76^o;cos87^o=sin3^o\). Vì \(3^o< 47^o< 76^o< 78^o\) nên \(sin3^o< sin47^o< sin76^o< sin78^o\). Vậy ta có thứ tự xếp sau: \(cos87^o< sin47^o< cos14^o< sin78^o\)
Đúng 0
Bình luận (0)
Sắp xếp các tỉ số lượng giác sau theo thứ tự tăng dần:
a
)
sin
78
°
,
cos
14
°
,
sin
47
°
,
cos...
Đọc tiếp
Sắp xếp các tỉ số lượng giác sau theo thứ tự tăng dần:
a ) sin 78 ° , cos 14 ° , sin 47 ° , cos 87 ° b ) tg 73 ° , cotg 25 ° , tg 62 ° , cotg 38 °
(Gợi ý: Bài này có 2 cách làm. Cách 1 là sử dụng máy tính. Cách 2 là sử dụng tính chất lượng giác của hai góc phụ nhau để đưa về cùng một tỉ số lượng giác rồi so sánh. Cách 2 nhanh hơn.)
a) Ta có:
sin 78 ° = cos 12 ° ; sin 47 ° = cos 43 ° V ì 12 ° < 14 ° < 43 ° < 87 ° n ê n cos 12 ° > cos 14 ° > cos 43 ° > cos 87 ° S u y r a : cos 87 ° < sin 47 ° < cos 14 ° < sin 78 ° b ) T a c ó : c o t g 25 ° = t g 65 ° ; c o t g 38 ° = t g 52 ° . V ậ y : c o t g 38 ° < t g 62 ° < c o t g 25 ° < t g 73 °
Đúng 0
Bình luận (0)
\(\frac{\sin^390^o-\cot^330^o-\cos^245^o+\tan20^o}{2\sqrt{7}+\sin108^o\cos32^o\tan64^o}\)