tích mình đi

ai tích mình

mình ko tích lại đâu

thanks

a. Gọi M' và N' là giao điểm của tia AM và BN với CD.

Ta có: ∠(M') = ∠A2(sole trong)

∠A1= ∠A2(gt)

⇒ ∠(M') = ∠A1nên ΔADM' cân tại D

* DM là phân giác của ∠(ADM' )

Suy ra: DM là đường trung tuyến (tính chất tam giác cân)

⇒ AM = MM'

∠(N') = ∠B1nên ΔBCN' cân tại C.

* CN là phân giác của ∠(BCN')

Suy ra: CN là đường trung tuyến (tính chất tam giác cân)

⇒ PN = NN'

Suy ra: MN là đường trung bình của hình thang ABN'M'

⇒ MN = M'N' (tính chất đường trung hình hình thang)

Hay MN//CD

b)MN=AB+M′N′/2 (tính chất đường trung bình của hình thang)

⇒MN=AB+M′D+CD+CN′/2(1)

Mà M′D=AD,CN′=BC. Thay vào (1)

MN=AB+AD+CD+BC/2=a+d+c+b/2

góc AMD=180 độ-góc MAD-góc MDA

\(=180^0-\dfrac{180^0-\widehat{BAD}}{2}-\dfrac{180^0-\widehat{ADC}}{2}\)

\(=180^0-\dfrac{1}{2}\widehat{ADC}-90^0+\dfrac{1}{2}\widehat{ADC}=90^0\)

Gọi giao của AM với DC là M'

Xét ΔDM'A có

DM là đường cao, là đường phân giác

nên ΔDM'A cân tại D

=>M là trung điểm của AM'

Gọi giao của BN với DC là N'

Ta có: \(\widehat{BNC}=180^0-\widehat{NBC}-\widehat{NCB}\)

\(=180^0-\dfrac{180^0-\widehat{ABC}}{2}-\dfrac{180^0-\widehat{BCD}}{2}\)

\(=180^0-90^0+\dfrac{1}{2}\widehat{ABC}-90^0+\dfrac{1}{2}\widehat{BCD}\)

=90 độ

Xét ΔCN'B có

CN vừa là đường cao, vừa là phân giác

nên ΔCN'B cân tại C

=>N là trug điểm của BN'

Xét hình thang ABN'M' có

M,N lần lượt là trung điểm của AM' và BN'

nen MN là đường trung bình

=>MN//CD

a) Gọi E, F lần lượt là giao điểm của AM và CD, BN và CD 

Ta có : AB//CD (gt) => E = A1 (so le trong)

 Mà A1 =A2 (gt) 

Nên A2 = E 

Xét ΔADE cân tại D, có DM là p/giác nên DM đồng thời là trung tuyến 

=>AM= EM 

Chứng minh tương tự, ta được : 

BN = FN 

Xét hình thang ABEF có : AM=BN(cm trên) 

BN=FN(cm trên) 

Do đó MN là đường TB của HÌNH thang ABEF 

=> MN= \(\frac{EF+AB}{2}\)

MN//AB//EF Vậy MN// CD(đpcm) 

b)Do ED= AD; BC=FC 

Mà ED + DC + CF = EF 

Nên AD + DC + BC = EF 

Lại có MN \(\frac{EF+AB}{2}\)(CM trên) 

Suy ra MN= \(\frac{AD+DC+BC+AB}{2}\)\(=\frac{a+b+c+d}{2}\)

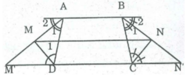
Gọi M' và N' là giao điểm của tia AM và BN với CD.

Ta có: ∠ (M') = ∠ A 2 (sole trong)

∠ A 1 =  ∠ A 2 (gt)

⇒  ∠ (M') =  ∠ A 1 nên ∆ ADM' cân tại D

* DM là phân giác của  ∠ (ADM' )

Suy ra: DM là đường trung tuyến (tính chất tam giác cân)

⇒ AM = MM'

∠ (N') =  ∠ B 1 nên  ∆ BCN' cân tại C.

* CN là phân giác của  ∠ (BCN')

Suy ra: CN là đường trung tuyến (tính chất tam giác cân)

⇒ BN = NN'

Suy ra: MN là đường trung bình của hình thang ABN'M'

⇒ MN // M'N' (tính chất đường trung hình hình thang)

Hay MN//CD