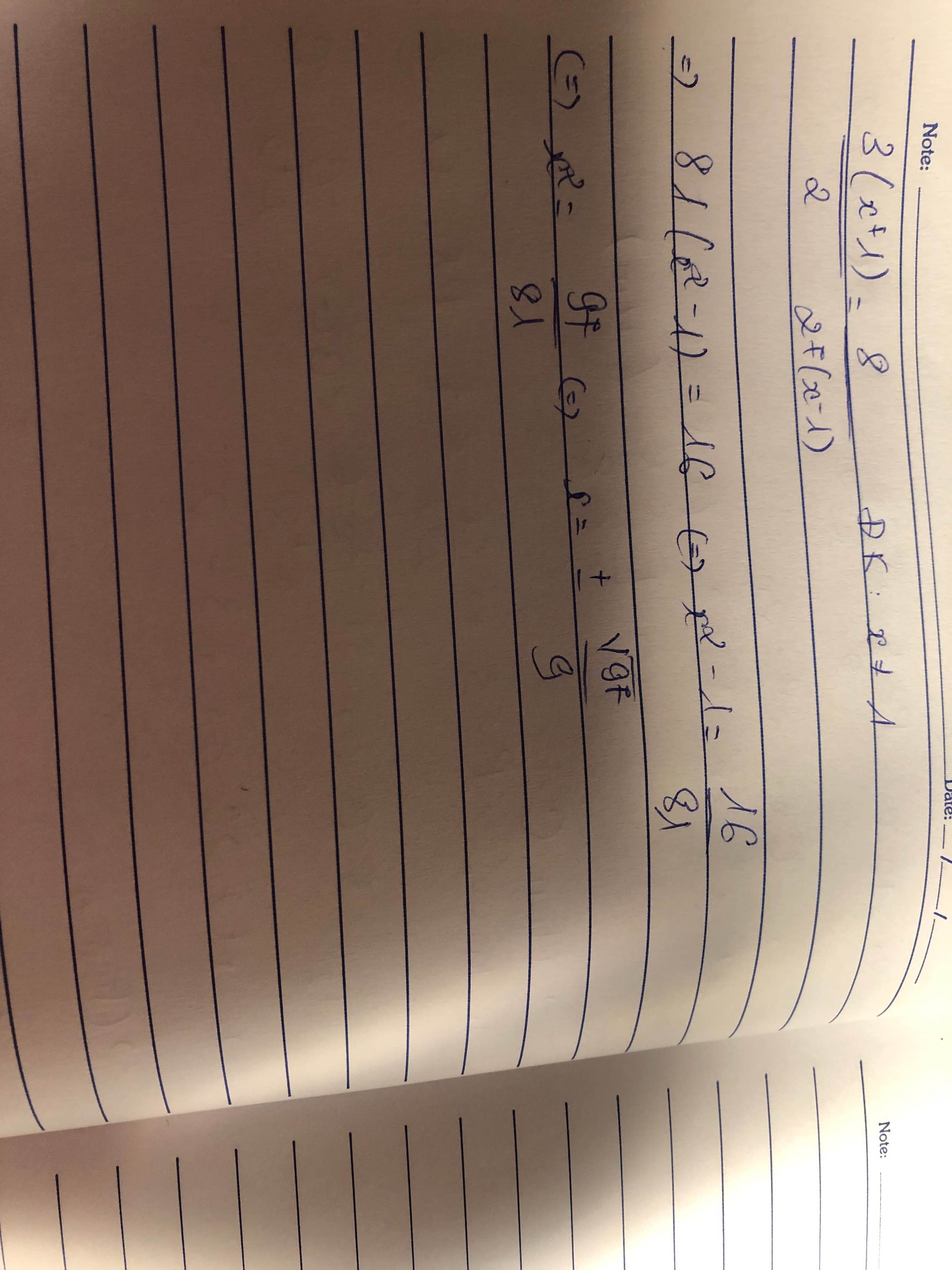\(\Leftrightarrow\dfrac{2}{2.4}+\dfrac{2}{4.6}+...+\dfrac{2}{\left(2x-2\right).2x}=\dfrac{11}{24}\)

\(\Leftrightarrow\dfrac{4-2}{2.4}+\dfrac{6-4}{4.6}+...+\dfrac{2x-\left(2x-2\right)}{\left(2x-2\right).2x}=\dfrac{11}{24}\)

\(\Leftrightarrow\dfrac{1}{2}-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{6}+...+\dfrac{1}{2x-2}-\dfrac{1}{2x}=\dfrac{11}{24}\)

\(\Leftrightarrow\dfrac{1}{2}-\dfrac{1}{2x}=\dfrac{11}{24}\)

\(\Leftrightarrow\dfrac{1}{2x}=\dfrac{1}{2}-\dfrac{11}{24}\)

\(\Leftrightarrow\dfrac{1}{2x}=\dfrac{1}{24}\)

\(\Rightarrow2x=24\)

\(\Rightarrow x=12\)

\(\left(1+\dfrac{1}{1.3}\right).\left(1+\dfrac{1}{2.4}\right).\left(1+\dfrac{1}{3.5}\right).........\left[1+\dfrac{1}{x.\left(x+2\right)}\right]=\dfrac{31}{16}\)

\(\Rightarrow\dfrac{2^2}{1.3}.\dfrac{3^2}{2.4}.\dfrac{4^2}{3.5}........\dfrac{\left(x+1\right)^2}{x.\left(x+2\right)}=\dfrac{31}{16}\)

\(\Rightarrow\dfrac{\left[2.3.4.............\left(x+1\right)\right].\left[2.3.4.............\left(x+1\right)\right]}{\left(1.2.3...................x\right).\left(3.4.5..........................\left(x+2\right)\right)}=\dfrac{31}{16}\)

\(\Rightarrow\dfrac{\left(x+1\right).2}{1.\left(x+2\right)}=\dfrac{31}{16}\)

\(\Leftrightarrow16.2\left(x+1\right)=31.\left(x+2\right)\)

\(\Rightarrow32x+32=31x+62\)

\(\Rightarrow x=30\)

Vậy x=30

Chúc bn học tốt

ĐKXĐ: \(x\notin\left\{0;-2\right\}\)

Ta có: \(\left(1+\dfrac{1}{1\cdot3}\right)\left(1+\dfrac{1}{2\cdot4}\right)\left(1+\dfrac{1}{3\cdot5}\right)\cdot...\cdot\left(1+\dfrac{1}{x\left(x+2\right)}\right)=\dfrac{31}{16}\)

\(\Leftrightarrow\dfrac{1\cdot3+1}{1\cdot3}+\dfrac{1+2\cdot4}{2\cdot4}+\dfrac{1+3\cdot5}{3\cdot5}\cdot...\cdot\dfrac{1+x\left(x+2\right)}{x\left(x+2\right)}=\dfrac{31}{16}\)

\(\Leftrightarrow\dfrac{2\cdot2}{1\cdot3}+\dfrac{3\cdot3}{2\cdot4}+\dfrac{4\cdot4}{3\cdot5}+...+\dfrac{\left(x+1\right)\left(x+1\right)}{x\left(x+2\right)}=\dfrac{31}{16}\)

\(\Leftrightarrow\dfrac{1\cdot2\cdot3\cdot...\cdot\left(x+1\right)}{1\cdot2\cdot3\cdot...\cdot x}\cdot\dfrac{2\cdot3\cdot4\cdot...\cdot\left(x+1\right)}{3\cdot4\cdot5\cdot...\cdot\left(x+2\right)}=\dfrac{31}{16}\)

\(\Leftrightarrow\left(x+1\right)\cdot\dfrac{2}{x+2}=\dfrac{31}{16}\)

\(\Leftrightarrow\dfrac{2x+2}{x+2}=\dfrac{31}{16}\)

\(\Leftrightarrow\dfrac{32x+32}{16\left(x+2\right)}=\dfrac{31\left(x+2\right)}{16\left(x+2\right)}\)

Suy ra: \(32x+32=31x+62\)

\(\Leftrightarrow x=30\)(thỏa ĐK)

Vậy: S={30}

\(\Leftrightarrow\dfrac{3}{1.4}+\dfrac{3}{4.7}+...+\dfrac{3}{x\left(x+3\right)}=\dfrac{375}{376}\)

\(\Leftrightarrow1-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{7}+...+\dfrac{1}{x}-\dfrac{1}{x+3}=\dfrac{375}{376}\)

\(\Leftrightarrow1-\dfrac{1}{x+3}=\dfrac{375}{376}\)

\(\Leftrightarrow\dfrac{1}{x+3}=1-\dfrac{375}{376}=\dfrac{1}{376}\)

\(\Rightarrow x+3=376\)

\(\Rightarrow x=373\)

a) Ta có: \(A=\left(\dfrac{x-5\sqrt{x}}{x-25}-1\right):\left(\dfrac{25-x}{x+2\sqrt{x}-15}-\dfrac{\sqrt{x}+3}{\sqrt{x}+5}+\dfrac{\sqrt{x}-5}{\sqrt{x}-3}\right)\)

\(=\left(\dfrac{\sqrt{x}\left(\sqrt{x}-5\right)}{\left(\sqrt{x}-5\right)\left(\sqrt{x}+5\right)}-1\right):\left(\dfrac{25-x}{\left(\sqrt{x}+5\right)\left(\sqrt{x}-3\right)}-\dfrac{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}{\left(\sqrt{x}+5\right)\left(\sqrt{x}-3\right)}+\dfrac{\left(\sqrt{x}-5\right)\left(\sqrt{x}+5\right)}{\left(\sqrt{x}+5\right)\left(\sqrt{x}-3\right)}\right)\)

\(=\left(\dfrac{\sqrt{x}}{\sqrt{x}+5}-1\right):\left(\dfrac{25-x-\left(x-9\right)+x-25}{\left(\sqrt{x}+5\right)\left(\sqrt{x}-3\right)}\right)\)

\(=\left(\dfrac{\sqrt{x}}{\sqrt{x}+5}-\dfrac{\sqrt{x}+5}{\sqrt{x}+5}\right):\left(\dfrac{25-x-x+9+x-25}{\left(\sqrt{x}+5\right)\left(\sqrt{x}-3\right)}\right)\)

\(=\dfrac{\sqrt{x}-\sqrt{x}-5}{\sqrt{x}+5}:\dfrac{x+9}{\left(\sqrt{x}+5\right)\left(\sqrt{x}-3\right)}\)

\(=\dfrac{-5}{\sqrt{x}+5}\cdot\dfrac{\left(\sqrt{x}+5\right)\left(\sqrt{x}-3\right)}{x+9}\)

\(=\dfrac{-5\left(\sqrt{x}-3\right)}{x+9}\)

Bổ sung phần c và d luôn:

c, C = \(\dfrac{2}{5}\)

\(\Leftrightarrow\) \(\dfrac{x^2-1}{2x^2+3}\) = \(\dfrac{2}{5}\)

\(\Leftrightarrow\) 5(x² - 1) = 2(2x² + 3)

\(\Leftrightarrow\) 5x² - 5 = 4x² + 6

\(\Leftrightarrow\) x² = 11

\(\Leftrightarrow\) x² - 11 = 0

\(\Leftrightarrow\) (x - \(\sqrt{11}\))(x + \(\sqrt{11}\)) = 0

\(\Leftrightarrow\) \(\left[{}\begin{matrix}x-\sqrt{11}=0\\x+\sqrt{11}=0\end{matrix}\right.\)

\(\Leftrightarrow\) \(\left[{}\begin{matrix}x=\sqrt{11}\left(TM\right)\\x=-\sqrt{11}\left(TM\right)\end{matrix}\right.\)

d, Ta có: \(\dfrac{x^2-1}{2x^2+3}\) = \(\dfrac{x^2+\dfrac{3}{2}-\dfrac{5}{2}}{2\left(x^2+\dfrac{3}{2}\right)}\) = \(\dfrac{1}{2}\) - \(\dfrac{5}{4\left(x^2+\dfrac{3}{2}\right)}\)

C nguyên \(\Leftrightarrow\) \(\dfrac{5}{4\left(x^2+\dfrac{3}{2}\right)}\) nguyên \(\Leftrightarrow\) 5 \(⋮\) 4(x² + \(\dfrac{3}{2}\))

\(\Leftrightarrow\) 4(x² + \(\dfrac{3}{2}\)) \(\in\) Ư(5)

Xét các TH:

4(x² + \(\dfrac{3}{2}\)) = 5 \(\Leftrightarrow\) x² = \(\dfrac{-1}{4}\) \(\Leftrightarrow\) x² + \(\dfrac{1}{4}\) = 0 (Vô nghiệm)

4(x² + \(\dfrac{3}{2}\)) = -5 \(\Leftrightarrow\) x² = \(\dfrac{-11}{4}\) \(\Leftrightarrow\) x² + \(\dfrac{11}{4}\) = 0 (Vô nghiệm)

4(x² + \(\dfrac{3}{2}\)) = 1 \(\Leftrightarrow\) x² = \(\dfrac{-5}{4}\) \(\Leftrightarrow\) x² + \(\dfrac{5}{4}\) = 0 (Vô nghiệm)

4(x² + \(\dfrac{3}{2}\)) = -1 \(\Leftrightarrow\) x² = \(\dfrac{-7}{4}\) \(\Leftrightarrow\) x² + \(\dfrac{7}{4}\) = 0 (Vô nghiệm)

Vậy không có giá trị nào của x \(\in\) Z thỏa mãn C \(\in\) Z

Chúc bn học tốt! (Ko bt đề sai hay ko nữa :v)

1: \(=\left|\dfrac{-21+5}{35}\right|+\dfrac{5}{7}\cdot\dfrac{-2}{5}\)

\(=\dfrac{16}{35}+\dfrac{-2}{7}=\dfrac{16}{35}-\dfrac{10}{35}=\dfrac{6}{35}\)

2: =>4^x+1=16

=>x+1=2

=>x=1

a. x=5/6

\(a,\Rightarrow\left(x-\dfrac{1}{2}\right)^3=\dfrac{1}{27}=\left(\dfrac{1}{3}\right)^3\\ \Rightarrow x-\dfrac{1}{2}=\dfrac{1}{3}\Rightarrow x=\dfrac{5}{6}\\ b,\Rightarrow\left(\dfrac{3}{2}\right)^{2x-1}:\left(\dfrac{3}{2}\right)^9=\left(\dfrac{3}{2}\right)^4\\ \Rightarrow2x-1-9=4\\ \Rightarrow2x=14\Rightarrow x=7\\ c,\Rightarrow2^{x-1}+2^{x+2}=9\cdot2^5\\ \Rightarrow2^{x-1}\left(1+2^3\right)=9\cdot2^5\\ \Rightarrow2^{x-1}\cdot9=9\cdot2^5\\ \Rightarrow2^{x-1}=2^5\Rightarrow x-1=5\Rightarrow x=6\\ d,\Rightarrow\left(2x+1\right)^2=12+69=81\\ \Rightarrow\left[{}\begin{matrix}2x+1=9\\2x+1=-9\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=4\\x=-5\end{matrix}\right.\)

\(a,\dfrac{2}{3}+\left(x-\dfrac{1}{2}\right)^3=\dfrac{19}{27}\)

\(\left(x-\dfrac{1}{2}\right)^3=\dfrac{19}{27}-\dfrac{2}{3}\)

\(\left(x-\dfrac{1}{2}\right)^3=\dfrac{1}{27}\)

\(\Rightarrow\left(x-\dfrac{1}{2}\right)^3=\left(\dfrac{1}{3}\right)^3\)

\(\Rightarrow x-\dfrac{1}{2}=\dfrac{1}{3}\)

\(x=\dfrac{1}{2}+\dfrac{1}{3}\)

\(x=\dfrac{1}{5}\)

đấy nhá

b) Ta có: \(\left|x\right|-\dfrac{3}{4}=\dfrac{5}{3}\)

\(\Leftrightarrow\left|x\right|=\dfrac{5}{3}+\dfrac{3}{4}=\dfrac{20}{12}+\dfrac{9}{12}=\dfrac{29}{12}\)

\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{29}{12}\\x=-\dfrac{29}{12}\end{matrix}\right.\)

c) Ta có: \(\left|2x-\dfrac{1}{3}\right|+\dfrac{5}{6}=1\)

\(\Leftrightarrow\left|2x-\dfrac{1}{3}\right|=\dfrac{1}{6}\)

\(\Leftrightarrow\left[{}\begin{matrix}2x-\dfrac{1}{3}=\dfrac{1}{6}\\2x-\dfrac{1}{3}=\dfrac{-1}{6}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}2x=\dfrac{1}{6}+\dfrac{1}{3}=\dfrac{1}{2}\\2x=\dfrac{1}{6}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{1}{4}\\x=\dfrac{1}{12}\end{matrix}\right.\)