Cho đường tròn tâm O tiếp xúc với 2 tia Ax;Ay tại2 điểm B;C. Đường thẳng song song với Ax từ C cắt đường tròn O tại M .CM cắt AB tại N. Chứng minh rằng:
a, tam giác ANC đồng dạng với tam giác MNA
b, AN=NB
Cho nửa đường tròn (O) đường kính AB, trên nửa mặt phẳng bờ AB chứa nửa đường tròn đó, kẻ hai tia tiếp tuyến Ax, By với (O). Gọi (I) là đường tròn tiếp xúc với Ax tại C và tiếp xúc ngoài với nửa đường tròn (O) tại F. Kẻ tiếp tuyến CE với (O) (E là tiếp điểm, E khác A), AE cắt tia By tại D. Cho AB = 2R.
a) Tính AC.BD theo R. Chứng minh CE^2 = CF.CB.
b) Đường thẳng vuông góc với By tại D cắt OE tại J, CE cắt DF tại G. Chứng minh:
- DF là tiếp tuyến của (O).
- G là tâm của đường tròn nội tiếp tam giác OIJ
Cho nửa đường tròn (O) đường kính AB, trên nửa mặt phẳng bờ AB chứa nửa đường tròn đó, kẻ hai tia tiếp tuyến Ax, By với (O). Gọi (I) là đường tròn tiếp xúc với Ax tại C và tiếp xúc ngoài với nửa đường tròn (O) tại F. Kẻ tiếp tuyến CE với (O), (E là tiếp điểm, E khác A), AE cắt tia By tại D. Cho AB = 2R.
a). Tính AC.BD theo R. Chứng minh : CE2 = CF.CB.
b). Đường thẳng vuông góc với By tại D cắt OE tại J, CE cắt DF tại G.Chứng minh:
- DF là tiếp tuyến của (O).
- G là tâm của đường tròn nội tiếp tam giác OIJ.
Cho nửa đường tròn tâm O đường kính AB=2R. Trên cùng một nửa mặt phẳng bờ AB có chứa nửa đường tròn kẻ các tia tiếp tuyến Ax,By của đường tròn.Trên Ax,By lấy C,D sao cho CD=AC+BD. CMR: a,COD = 90* b, AB tiếp xúc với đường trong ngoại tiếp tam giác COD
Cho nửa đường tròn (O;R) đường kính AB=2R.Kẻ 2 tiếp tuyến Ax,By của nửa đường tròn (O) .Tiếp tuyến thứ 3 tiếp xúc với nửa đường tròn O tại M cắt Ax,By lần lượt tại D và E.a)Chứng minh tâm giác DOE vuông.b)Chứng minh AD.BE=R^2
cho 2 đường tròn o và o tiếp xúc ngoài tại a. Trên tia Ax vuông góc với OO' lấy một điểm M. Vẽ tiếp tuyến MB với đường tròn (O),tiếp tuyến MC với đường tròn (O'), tia BO cắt tia CO tại N a. Chứng minh : MA=MB=MC b. Chứng minh tứ giác MBNC nội tiếp c. Chứng minh BC ⊥ MN
a.Có MA,MB là tiếp tuyến của (O) cắt nhau tại M (gt)
=> MA=MB
Có MA,MC là tiếp tuyến của (O') cắt nhau tại M (gt)
=> MA=MC
Bắc cầu ta được MA=MB=MC
Cho góc xAy khác góc bẹt, điểm B thuộc tia Ax. Hãy dựng đường tròn (O) tiếp xúc với Ax tại B và tiếp xúc với Ay.
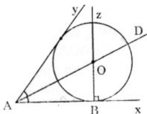
Đường tròn (O) tiếp xúc với hai tia Ax và Ay nên tâm O của (O) nằm trên tia phân giác của góc xAy
Cho góc xAy khác góc bẹt, điểm B thuộc tia Ax. Hãy dựng đường tròn (O) tiếp xúc với Ax tại B và tiếp xúc với Ay.
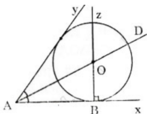
Đường tròn (O) tiếp xúc với hai tia Ax và Ay nên tâm O của (O) nằm trên tia phân giác của góc xAy. (Xem lại Bài 28 trang 116 SGK Toán 9 Tập 1) . Do đó ta có cách dựng:
- Dựng tia phân giác At của góc xAy.
- Dựng đường thẳng Bz qua B và vuông góc với tia Ax.
- Giao điểm O của At và Bz là tâm của đường tròn cần dựng.
- Dựng đường tròn tâm O, bán kính R = OB, ta được đường tròn cần dựng.
Cho đường tròn tâm O đường kính AB = 2R và C là một điểm thuộc đường tròn khác A , B, M là điểm chính giữa của cung nhỏ AC. Kẻ Ax tiếp xúc với (O). Tia BC cắt Ax tại Q, tia AM cắt BQ tại N.
a) Chứng minh các tam giác BaN, MCN cân
b) Khi MB = MQ, tính BC theo R
a ) .Xét t/g ABM và t/g NBM có:
AB là đường kính của đường trong (O)
nên : góc ABM = góc NMB = 90 độ
M là điểm chính giữa của cung nhỏ AC
nên : góc ABM = góc MBN=>góc BAM = góc BNM
=> t/g BAN cân tại đỉnh B
Tứ giác AMCB nội tiếp
=> góc BAM = góc MCN ( cùng bù với góc MCB )
=> góc MCN = góc MNC ( cùng bằng góc BAM)
=> t/g MCN cân tại đỉnh M
b) .
Xét t/g MCB và t/g MNQ ta có:
MC = MN ( theo cm trên : MCN cân) ; MB =MQ ( theo giả thiết)
góc BMC = góc MNQ ( vì : góc MCB = góc MNC ; góc MBC = góc MQN ).
=> t/g MCB = t/g MNQ ( c.g.c ) => BC = NQ
Xét t/g vuông ABQ ta có:
AC vuông góc BQ => \(AB^2=BC.BQ=BC.\left(BN+NQ\right)\)
=> \(AB^2=BC.\left(AB+AC\right)=BC.\left(BC+2R\right)\)
=> \(4R^2=BC\left(BC+2R\right)\Rightarrow BC=\left(\sqrt{5}-1\right)R\)
Cho góc xAy khác góc bẹt, điểm B thuộc tia Ax. Hãy dựng đường tròn (O) tiếp xúc với Ax tại B và tiếp xúc với Ay ?

Cách dựng:
– Dựng tia phân giác At của góc xAy
– Dựng đường thẳng Bz qua B và vuông góc với tia Ax
– Giao điểm O của At và Bz là tâm của đường tròn cần dựng.
– Dựng đường tròn tâm O, bán kính R = OB, ta được đường tròn cần dựng.