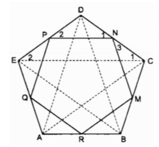
Xét △ ABC và  △  BCD:

AB = BC (gt)

∠ B = ∠ C (gt)

BC = CD (gt)

Do đó:  △  ABC =  △  BCD (c.g.c)

⇒ AC = BD (1)

Xét  △  BCD và  △  CDE:

BC = CD (gt)

∠ C =  ∠ D (gt)

CD = DE (gt)

Do đó:  △  BCD =  △  CDE (c.g.c) ⇒ BD = CE (2)

Xét  △ CDE và  △  DEA:

CD = DE (gt)

∠ D =  ∠ E (gt)

DE = EA (gt)

Do đó:  △  CDE =  △  DEA (c.g.c) ⇒ CE = DA (3)

Xét △  DEA và  △  EAB:

DE = EA (gt)

∠ E =  ∠ A (gt)

EA = AB (gt)

Do đó:  △  DEA =  △  EAB (c.g.c) ⇒ DA = EB (4)

Từ (1), (2), (3), (4) suy ra: AC = BD = CE = DA = EB

Trong  △  ABC ta có RM là đường trung bình

⇒ RM = 1/2 AC (tính chất đường trung bình của tam giác)

Mặt khác, ta có: Trong Δ BCD ta có MN là đường trung bình

⇒ MN = 1/2 BD (tính chất đường trung bình của tam giác)

Trong  △  CDE ta có NP là đường trung bình

⇒ NP = 1/2 CE (tính chất đường trung bình của tam giác)

Trong  △  DEA ta có PQ là đường trung bình

⇒ PQ = 1/2 DA (tính chất đường trung bình của tam giác)

Trong  △  EAB ta có QR là đường trung bình

⇒ QR = 1/2 EB (tính chất đường trung bình của tam giác)

Suy ra: MN = NP = PQ = QR = RM

Ta có:  ∠ A =  ∠ B =  ∠ C =  ∠ D =  ∠ E = ((5-2 ). 180 0 )/5 =  108 0

△  DPN cân tại D

⇒ ∠ (DPN) =  ∠ (DNP) = ( 180 0 -  ∠ D )/2 = ( 180 0  -  108 0 )/2 =  36 0

△  CNM cân tại C

⇒  ∠ (CNM) =  ∠ (CMN) = ( 180 0 -  ∠ D )/2 = ( 180 0  -  108 0 )/2 =  36 0

∠ (ADN) +  ∠ (PNM) +  ∠ (CNM) =  180 0

⇒  ∠ (PNM) =  180 0  - ( ∠ (ADN) +  ∠ (CNM) )

            = 180 0  - ( 36 0  –  36 0 ) =  108 0

△  BMR cân tại B

⇒  ∠ (BMR) =  ∠ (BRM) = ( 180 0 -  ∠ B )/2 = ( 180 0  -  108 0 )/2 =  36 0

∠ (CMN) +  ∠ (BRM) +  ∠ (BMR) =  180 0

⇒  ∠ (NMR) =  180 0  - ( ∠ (CMN) +  ∠ (BMR) )

            =  180 0  - ( 36 0  –  36 0 ) =  108 0

△  ARQ cân tại A

⇒  ∠ (ARQ) =  ∠ (AQR) = ( 180 0 -  ∠ A )/2 = ( 180 0  -  108 0 )/2 =  36 0

∠ (BRM) +  ∠ (MRQ) +  ∠ (ARQ) =  180 0

⇒  ∠ (MRQ) =  180 0  - ( ∠ (BRM) +  ∠ (ARQ) )

            = 180 0  - ( 36 0  –  36 0 ) =  108 0

△  QEP cân tại E

⇒  ∠ (EQP) =  ∠ (EPQ) = ( 180 0 -  ∠ E )/2 = ( 180 0  -  108 0 )/2 =  36 0

∠ (AQR) + ∠ (RQP) +  ∠ (EQP) =  180 0

⇒  ∠ (RQP) =  180 0  - ( ∠ (AQR) +  ∠ (EQP) )

            =  180 0  - ( 36 0  –  36 0 ) =  108 0

∠ (EQP) +  ∠ (QPN) +  ∠ (DPN) =  180 0

⇒  ∠ (QPN) =  180 0  - ( ∠ (EPQ) +  ∠ (DPN) )

            =  180 0  - ( 36 0  –  36 0 ) =  108 0

Suy ra :  ∠ (PNM) =  ∠ (NMR) =  ∠ (MRQ) =  ∠ (RQP) =  ∠ (QPN)

Vậy MNPQR là ngũ giác đều.

1.

a, Trọng Tâm G: \(\left\{{}\begin{matrix}x_G=\dfrac{x_A+x_B+x_C}{3}=\dfrac{8}{3}\\y_G=\dfrac{y_A+y_B+y_C}{3}=\dfrac{8}{3}\end{matrix}\right.\)

\(\Rightarrow G=\left(\dfrac{8}{3};\dfrac{8}{3}\right)\)

b, \(ABCD\) là hình bình hành \(\Leftrightarrow\vec{AB}=\vec{DC}\)

\(\Leftrightarrow\left\{{}\begin{matrix}x_B-x_A=x_C-x_D\\y_B-y_A=y_C-y_D\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}x_D=0\\y_D=6\end{matrix}\right.\)

\(\Rightarrow D=\left(0;6\right)\)

c, \(\vec{AM}=3\vec{BC}\Leftrightarrow\left\{{}\begin{matrix}x_M=x_A+3\left(x_C-x_B\right)=-6\\y_M=y_A+3\left(y_C-y_B\right)=14\end{matrix}\right.\)

\(\Rightarrow M=\left(-6;14\right)\)