a)3x-2≥x+6

<=>3x-x≥6+2

<=>2x≥8

<=>x≥4

tập nghiệm của phương trình là 

\(S=\left\{xIx\ge4\right\}\)

biểu diễn tập nghiệm trên trục số

b)(3x-6)-(-2x-1)≥0

<=>3x-6++1≥0

<=>3x+2x≥6-1

<=>5x≥5

<=>x≥1

tập nghiệm của phương trình là 

\(S=\left\{xIx\ge1\right\}\)

a: =>2x>=8

=>x>=4

b: =>3x-6+2x+1>=0

=>5x-5>=0

=>x>=1

x + 2 > 1

⇔ x > 1 – 2

⇔ x > -1.

Vậy bất phương trình có nghiệm x > -1.

a, \(\frac{2\left(2-3x\right)}{5}< \frac{4-2x}{3}\Leftrightarrow\frac{4-6x}{5}-\frac{4-2x}{3}< 0\)

\(\Leftrightarrow\frac{12-18x-20+10x}{15}< 0\Leftrightarrow-8x-8< 0\Leftrightarrow x>-1\)vì 15 > 0 

-/-/-(----|------> 

    -1    0                           

Vậy tập ngiệm của bft là S = { x | x > -1 }

b, \(x\left(9x+1\right)+1\le\left(1-3x\right)^2\Leftrightarrow9x^2+x+1\le1-6x+9x^2\)

\(\Leftrightarrow7x\le0\Leftrightarrow x\le0\)

-------]--/-/-/-/-->

       0

Vậy tập nghiệm của bft là S = { x | x =< 0 } 

\(\frac{2\cdot\left(2-3x\right)}{5}< \frac{4-2x}{3}\)   

\(\frac{4-6x}{5}< \frac{4-2x}{3}\)   

\(\left(4-6x\right)\cdot3< \left(4-2x\right)\cdot5\)   

\(12-18x< 20-10x\)   

\(10x-18x< 20-12\)   

\(-8x< 8\)   

\(x>-1\)   

\(x\cdot\left(9x+1\right)+1\le\left(1-3x\right)^2\)   

\(9x^2+x+1\le9x^2-6x+1\)   

\(x\le-6x\)   

\(x+6x\le0\)   

\(7x\le0\)   

\(x\le0\)

biểu diễn bn ơi

a) Ta có: 2. (-2) ≤ 3 nên -2 có là nghiệm của bất phương trình

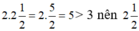+)  không là nghiệm của bất phương trình ,

+) 2π > 3 nên π không là nghiệm của bất phương trình.

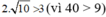+)  nên √10 không là nghiệm của bất phương trình,

Các số là nghiệm của bất phương trình trên là: -2;

Các số không là nghiệm của bất phương trình trên là: 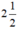; π; √10

b)2x ≤ 3 ⇔ x ≤ 3/2

Biểu diễn tập nghiệm trên trục số là:

2:

a: =>x-4>=0

=>x>=4

b: =>x+1>0

=>x>-1

=>4x>16

=>x>4

\(a,3x-11>5-x\\ \Leftrightarrow3x+x>5+11\\ \Leftrightarrow4x< 16\\ \Leftrightarrow x>4\)

Vậy bất phương trình có nghiệm là: \(S=\left\{x|x>4\right\}\)

biểu diễn

`(x+4)/5 - (x-2)/3 > 2`

`=> (3x+12 - 5x + 10)/15 > 2`

`=> 24 - 2x > 30`

`=> -2x > 6`

`=> x < -3`.

\(\dfrac{x+4}{5}\) \(-\) \(\dfrac{x-2}{3}\) \(>\) \(2\) 

\(=\) \(\dfrac{3x+12-5x+10}{15}\) \(>\) \(2\) 

\(=\) \(24-2x>30\)

\(=\) \(-2x>6\) 

\(=\) \(x< -3\)

x – 1 < 3

⇔ x < 3 + 1 (Chuyển vế và đổi dấu hạng tử -1)

⇔ x < 4

Vậy bất phương trình có nghiệm x < 4.

a: =>2x^2+8x-3x-12<2x^2+2

=>5x<14

=>x<14/5

b: =>\(\dfrac{9x-3-\left(5x+1\right)\left(x-2\right)}{3\left(x-2\right)}-4>0\)

=>\(\dfrac{9x-3-5x^2+10x-x+2-12\left(x-2\right)}{3\left(x-2\right)}>0\)

=>\(\dfrac{-5x^2+18x-1-12x+24}{3\left(x-2\right)}>0\)

=>\(\dfrac{-5x^2+6x+23}{x-2}>0\)

TH1: x-2>0 và -5x^2+6x+23>0

=>x>2 và \(\dfrac{3-2\sqrt{31}}{5}< x< \dfrac{3+2\sqrt{31}}{5}\)

=>\(2< x< \dfrac{3+2\sqrt{31}}{5}\)

TH2: x-2<0 và -5x^2+6x+23<0

=>x<2 và \(\left[{}\begin{matrix}x< \dfrac{3-2\sqrt{31}}{5}\\x>\dfrac{3+2\sqrt{31}}{5}\end{matrix}\right.\)

=>\(x< \dfrac{3-2\sqrt{31}}{5}\)

1: \(\Leftrightarrow x^2+6x+9-6x+3>x^2-4x\)

=>-4x<12

hay x>-3

2: \(\Leftrightarrow6+2x+2>2x-1-12\)

=>8>-13(đúng)

4: \(\dfrac{2x+1}{x-3}\le2\)

\(\Leftrightarrow\dfrac{2x+1-2x+6}{x-3}< =0\)

=>x-3<0

hay x<3

6: =>(x+4)(x-1)<=0

=>-4<=x<=1