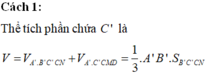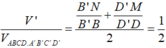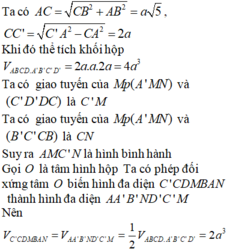Cho hình hộp chữ nhật ABCD.A'B'C'D' có cạnh AB=a√2; AD=a√6 và AA'=2a√2. Tính côsin của góc giữa đường thẳng B'D và mặt phẳng (B'D'C).

Những câu hỏi liên quan
Cho hình hộp chữ nhật ABCD.ABCD có cạnh ABa, BC3a, AC
26
a. Thể tích của khối hộp chữ nhật đó là A. 6
a
3
B. 3
a
3
C. 12
a
3
D. 4
a
3
Đọc tiếp
Cho hình hộp chữ nhật ABCD.A'B'C'D' có cạnh AB=a, BC=3a, A'C= 26 a. Thể tích của khối hộp chữ nhật đó là
A. 6 a 3
B. 3 a 3
C. 12 a 3
D. 4 a 3
Cho hình hộp chữ nhật ABCD.ABCD có AB a, AD 2a, AC
6
a. Thể tích khối hộp chữ nhật ABCD.ABCD bằng: A.
3
a
3
3
B.
2
a
3
3
C.
2
a
3
D.
2...
Đọc tiếp
Cho hình hộp chữ nhật ABCD.A'B'C'D' có AB = a, AD = 2a, AC' = 6 a. Thể tích khối hộp chữ nhật ABCD.A'B'C'D' bằng:
A. 3 a 3 3
B. 2 a 3 3
C. 2 a 3
D. 2 3 a 3
Phương pháp:
Công thức tính thể tích khối hộp chữ nhật ABCD.A'B'C'D' là V = AA'.AB.AD
Cách giải:
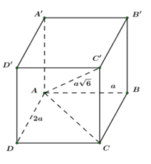
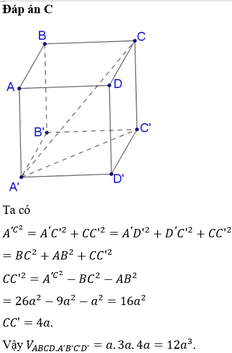
Ta có: ![]() (định lý Pitago)
(định lý Pitago)
Xét tam giác ACC’ vuông tại C ta có:
![]()
![]()
![]()
Chọn C.
Đúng 0
Bình luận (0)
Cho hình hộp chữ nhật ABCD.ABCD có ABa, AD2a, AA3a. Thể tích khối cầu ngoại tiếp hình hộp chữ nhật ABCD.ABCD là
Đọc tiếp
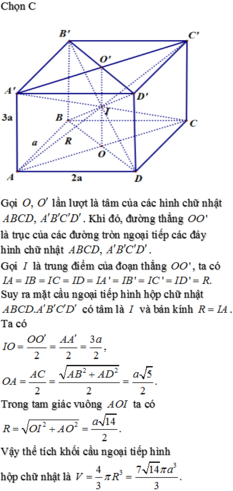
Cho hình hộp chữ nhật ABCD.A'B'C'D' có AB=a, AD=2a, AA'=3a. Thể tích khối cầu ngoại tiếp hình hộp chữ nhật ABCD.A'B'C'D' là
![]()
![]()
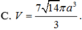
![]()
Cho hình hộp chữ nhật ABCD.ABCD có AB 2cm, AD 3cm, AA 4cm. Thể tích hình hộp chữ nhật ABCD.ABCD ? A. 12
c
m
3
B. 24
c
m
3
C. 18
c
m
3
D. 15
c
m
3
Đọc tiếp
Cho hình hộp chữ nhật ABCD.A'B'C'D' có AB = 2cm, AD = 3cm, AA' = 4cm. Thể tích hình hộp chữ nhật ABCD.A'B'C'D' ?
A. 12 c m 3
B. 24 c m 3
C. 18 c m 3
D. 15 c m 3
Ta có:
V = A B . A D . A A ' = 2 . 3 . 4 = 24 c m 3
Chọn đáp án B.
Đúng 0
Bình luận (0)
Cho hình hộp chữ nhật ABCD.ABCD có AB 2cm, AD 3cm, AA 4cm. Thể tích hình hộp chữ nhật ABCD.ABCD ? A. 12
c
m
3
B. 24
c
m
3
C. 18
c
m
3
D. 15
c
m
3
Đọc tiếp
Cho hình hộp chữ nhật ABCD.A'B'C'D' có AB = 2cm, AD = 3cm, AA' = 4cm. Thể tích hình hộp chữ nhật ABCD.A'B'C'D' ?
A. 12 c m 3
B. 24 c m 3
C. 18 c m 3
D. 15 c m 3
Ta có: V = AB.AD.AA' = 2.3.4 = 24 ( c m 3 )
Chọn đáp án B.
Đúng 0
Bình luận (0)
Cho hình hộp chữ nhật ABCD.ABCD có AB a, BC 2a, AC a. Điểm N thuộc cạnh BB’ sao cho BN 2NB, điểm M thuộc cạnh DD’ sao cho DM 2MD. Mp(AMN) chia hình hộp chữ nhật làm hai phần, tính thể tích phần chứa điểm C. A. 4
a
3
B.
a
3
C. 2
a
3
D. 3
a
3
Đọc tiếp
Cho hình hộp chữ nhật ABCD.A'B'C'D' có AB = a, BC = 2a, AC' = a. Điểm N thuộc cạnh BB’ sao cho BN = 2NB', điểm M thuộc cạnh DD’ sao cho D'M = 2MD. Mp(A'MN) chia hình hộp chữ nhật làm hai phần, tính thể tích phần chứa điểm C'.
A. 4 a 3
B. a 3
C. 2 a 3
D. 3 a 3
Đáp án là C
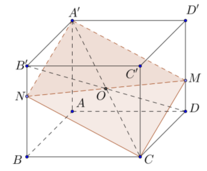
Nhận xét: B'NDM là hình bình hành (B'N = DM, B'N//DM)
=> MN ∩ B'D = O là trung điểm của mỗi đoạn nên O cũng là trung điểm của đường chéo A'C.
Vậy thiết diện tạo bởi mặt (A'MN) và hình chóp là hình bình hành A'NCM.
Ta có: ![]()
Cách 1:
Thể tích phần chứa C' là
![]()
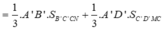
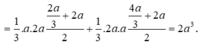
Cách 2: Áp dụng công thức tính nhanh
Gọi thể tích phần chứa C' là V'.
Ta có: 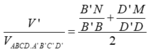
![]()
Cách 3: Nhận xét nhanh do đa diện chứa C' đối xứng với đa diện không chứa C' qua O nên thể tích của hai phần này bằng nhau, suy ra 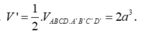
Đúng 0
Bình luận (0)
Cho hình hộp chữ nhật ABCD.ABCD có ABa, BC2a, ACa. Điểm N thuộc cạnh BB’ sao cho BN2NB, điểm M thuộc cạnh DD’ sao cho DM2MD. Mp(AMN) chia hình hộp chữ nhật làm hai phần, tính thể tích phần chứa điểm C. A.
4
a
3
B.
a
3
C.
2
a
3
D.
3
a
3
Đọc tiếp
Cho hình hộp chữ nhật ABCD.A'B'C'D' có AB=a, BC=2a, AC'=a. Điểm N thuộc cạnh BB’ sao cho BN=2NB', điểm M thuộc cạnh DD’ sao cho D'M=2MD. Mp(A'MN) chia hình hộp chữ nhật làm hai phần, tính thể tích phần chứa điểm C'.
A. 4 a 3
B. a 3
C. 2 a 3
D. 3 a 3
Cho hình hộp chữ nhật ABCD.ABCD có ABa, BC2a, ACa . Điểm N thuộc cạnh BB’ sao cho BN2NB, điểm M thuộc cạnh DD’ sao cho DM2MD. mp(AMN) chia hình hộp chữ nhật làm hai phần, tính thể tích phần chứa điểm C A.
4
a
3
B.
a
3
C.
2
a
3...
Đọc tiếp
Cho hình hộp chữ nhật ABCD.A'B'C'D' có AB=a, BC=2a, AC'=a . Điểm N thuộc cạnh BB’ sao cho BN=2NB', điểm M thuộc cạnh DD’ sao cho D'M=2MD. mp(A'MN) chia hình hộp chữ nhật làm hai phần, tính thể tích phần chứa điểm C'
A. 4 a 3
B. a 3
C. 2 a 3
D. 3 a 3
Đáp án là C
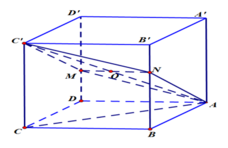
Ta có
![]()
![]()
Khi đó thể tích khối hộp
![]()
Ta có giao tuyến của (A'MN) và (C'D'DC) là C'M
Ta có giao tuyến của (A'MN) và (B'C'CB) là CN
Suy ra AMC'N là hình bình hành
Gọi O là tâm hình hộp. Ta có phép đối xứng tâm O biến hình đa diện C'CDMBAN thành hình đa diện AA'B'ND'C'M
![]()
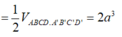
Đúng 0
Bình luận (0)
Cho hình hộp chữ nhật ABCD.ABCD có ABa, BC2a, ACa. Điểm N thuộc cạnh BB’ sao cho BN2NB, điểm M thuộc cạnh DD’ sao cho DM2MD. Mp (AMN) chia hình hộp chữ nhật làm hai phần, tính thể tích phần chứa điểm C A.
4
a
3
B.
a
3
C.
2
a
3
D.
3
a
3
Đọc tiếp
Cho hình hộp chữ nhật ABCD.A'B'C'D' có AB=a, BC=2a, AC'=a. Điểm N thuộc cạnh BB’ sao cho BN=2NB', điểm M thuộc cạnh DD’ sao cho D'M=2MD. Mp (A'MN) chia hình hộp chữ nhật làm hai phần, tính thể tích phần chứa điểm C'
A. 4 a 3
B. a 3
C. 2 a 3
D. 3 a 3
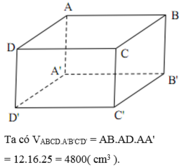
Cho hình hộp chữ nhật ABCD.A'B'C'D' có AB = 12cm, AD = 16cm, AA' = 25cm. Tính thể tích hình hộp chữ nhật ABCD.A'B'C'D'.