Cho \(\Delta ABC\) cân tại A, có 2 đường phân giác BD và CE cắt nhau ở H. M là trung điểm của BC. Chứng minh rằng A,H,M thẳng hàng

Những câu hỏi liên quan
Cho tam giác ABC cân tại A ( Â nhọn) có 2 đường cao BD và CE cắt nhau tại H
a) Chứng minh : AH là tia phân giác của Â
b) Chứng minh : 2 tam giác BEC và CEB bằng nhau
c) Gọi M là Trung Điểm BC. Chứng minh 3 điểm A, H , M thẳng hàng
Vẽ hình và giải dùm mình nha :v
Hình bạn tự vẽ nhé !
a) Vì \(BD;CE\)là hai đường cao mà \(BD;CE\)cắt nhau tại \(H\)
\(\Rightarrow H\)là trực tâm của \(\Delta ABC\)
\(\Rightarrow AH\)là đường cao thứ ba mà \(\Delta ABC\left(AB=AC\right)\)nên \(AH\)đồng thời là tia phân giác của \(\widehat{BAC}\)(1)
b) Xét \(\Delta BEC;\Delta CDB\)có :
\(\widehat{BEC}=\widehat{CDB}=90^o\left(gt\right)\)
\(\widehat{CBE}=\widehat{BCD}\)(vì tam giác ABC cân A)\(\)
\(BC\)cạnh huyền chung
Từ 3 điều trên \(\Rightarrow\Delta BEC=\Delta CDB\left(CH-GN\right)\)
c) Vì \(M\)là trung điểm của \(BC\)\(\Rightarrow BM=CM\)\(\Rightarrow AM\)là đường trung tuyến đồng thời là đường phân
giác của \(\widehat{BAC}\)(2)
Từ (1) và (2)\(\Rightarrow AH;AM\)là tia phân giác của \(\widehat{BAC}\)\(\Rightarrow A;H;M\)thẳng hàng
k cho mình nhé !
Đúng 0
Bình luận (0)
Cho tam giác ABC cân tại A ( Â nhọn ) có 2 đường cao BD và CE cắt nhau tại H
a) chứng minh AH là tia phân giác của Â
b) chứng minh tam giác BEC = tam giác CDB
c) gọi M là trung điểm của BC . Chứng minh 3 điểm A , H , M thẳng hàng
Làm hộ câu c) ạ
bạn cm AM là trung tuyến
đồng thời dựa vào tam giác ABC cân và AH là đường cao ta cm được AH là trung tuyến
suy ra AM trùng với AH
vậy A,H,M thẳng hàng
Đúng 0
Bình luận (0)
Xét \(\Delta AMB\) và \(\Delta AMC\)có:
\(AB=AC\)
\(AM\) là cạnh chung
\(BM=CM\)
\(\Rightarrow\Delta AMB=\Delta AMC\left(c.c.c\right)\)
\(\Rightarrow\widehat{AMB}=\widehat{AMC}=\frac{180^0}{2}=90^0\)
Do BD và CE là 2 đường cao cắt nhau tại H nên AH là đường cao mà AM cũng là đường cao nên A,H,M thẳng hàng.
Đúng 0
Bình luận (0)
cho tam giác ABC cân tại a đường phân giác BD và CE cắt nhau tại D a) chứng minh BD=CE b) DE song song BC c) gọi H là điểm chung của BC chứng minh AOH thẳng hàng
a:
BD là phân giác của \(\widehat{ABC}\)
=>\(\widehat{ABD}=\widehat{CBD}=\dfrac{1}{2}\cdot\widehat{ABC}\left(1\right)\)
CE là phân giác của \(\widehat{ACB}\)
=>\(\widehat{ACE}=\widehat{BCE}=\dfrac{1}{2}\cdot\widehat{ACB}\left(2\right)\)
ΔABC cân tại A
=>\(\widehat{ABC}=\widehat{ACB}\left(3\right)\)
Từ (1),(2),(3) suy ra \(\widehat{ABD}=\widehat{CBD}=\widehat{ACE}=\widehat{ECB}\)
Xét ΔABD và ΔACE có
\(\widehat{ABD}=\widehat{ACE}\)
AB=AC
\(\widehat{BAD}\) chung
Do đó: ΔABD=ΔACE
=>BD=CE
b: ΔABD=ΔACE
=>AD=AE
Xét ΔABC có \(\dfrac{AE}{AB}=\dfrac{AD}{AC}\)
nên DE//BC
c: Sửa đề: Gọi H là trung điểm của BC
Xét ΔOBC có \(\widehat{OBC}=\widehat{OCB}\left(cmt\right)\)
nên ΔOCB cân tại O
=>OB=OC
=>O nằm trên đường trung trực của BC(1)
AB=AC
=>A nằm trên đường trung trực của BC(2)
HB=HC
=>H nằm trên đường trung trực của BC(3)
Từ (1),(2),(3) suy ra A,O,H thẳng hàng
Đúng 3
Bình luận (0)
Cho tam giác ABC cân tại A(góc A=90).có BD ,CE là hai đường cao của tam giác(D thuộc AC,E thuộc AB).đường thẳng BD cắt CE tại H
a. Chứng minh BD=CE
b. Chứng minh tam giác ADE cân và DE song song với BC
c. Gọi M là trung điểm của BC. Chứng minh 3 điểm A,H,M thẳng hàng
Giúp mình vẽ hình và giải bài toán với ạ
Cho tam giác ABC cân tại A. Các đường cao BD và CE cắt nhau tại H
Gọi M là trung điểm của HC, N là trung điểm của HB, I là giao điểm của BM và CN. Chứng minh 3 điểm A,H,I thẳng hàng
Cho tam giác ABC cân tại A ( góc A nhọn ) kẻ hai đường cao BD và CE cắt nhau tại một H ( D thuộc AC; E thuộc AC )
a) Chứng minh AH là tia phân giác của góc A
b) Chứng minh tam giác BEC = tam giác CDB
c) Gọi M là trung điểm của BC. Chứng minh ba điểm A, H, M thẳng hàng.
Cho tam giác ABC cân tại A các đường cao BD và CE cắt nhau tại H Chứng minh AD = AE cho AB = 10 cm AD = 6 cm Tính khoảng cách từ điểm B đến cạnh AC biết Bac = 50 độ tính BC Gọi M là trung điểm của BC Chứng minh ba điểm A M N thẳng hàng.
a: Xét ΔABD vuông tại D và ΔACE vuông tại E có
AB=AC
góc BAD chung
Do đó: ΔABD=ΔACE
Suy ra: AD=AE
b: \(BD=\sqrt{10^2-6^2}=8\left(cm\right)\)
d: Xét ΔHBC có \(\widehat{HBC}=\widehat{HCB}\)
nên ΔHBC cân tại H
=>HB=HC
hay H nằm trên đường trung trực của BC(1)
Ta có: ΔABC cân tại A
mà AM là đường trung tuyến
nên AM là đường trung trực của BC(2)
Từ (1) và (2) suy ra A,H,M thẳng hàng
Đúng 2
Bình luận (0)
Cho tam giác ABC nội tiếp đưòng tròn (O), hai đường cao BD và CE cắt nhau tại H. Vẽ đường kính AFa, Tứ giác BFCH là hình gì?b, Gọi M là trung điểm của BC. Chứng minh rằng ba điểm H, M, F thẳng hàngc, Chứng minh OM
1
2
AH
Đọc tiếp
Cho tam giác ABC nội tiếp đưòng tròn (O), hai đường cao BD và CE cắt nhau tại H. Vẽ đường kính AF
a, Tứ giác BFCH là hình gì?
b, Gọi M là trung điểm của BC. Chứng minh rằng ba điểm H, M, F thẳng hàng
c, Chứng minh OM = 1 2 AH
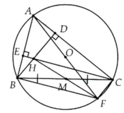
a,Chứng minh được BFCH là hình bình hành
b, Sử dụng kết quả câu a), suy ra HF đi qua M
c, Chú ý: OM là đường trung bình của ∆AHF => ĐPCM
Đúng 0
Bình luận (0)
Cho tam giác ABC có ba góc nhọn ( AB<AC). M là trung điểm của BC. Qua M kẻ đường vuông góc với tia phân giác của góc A tại H( H không trùng với M ), đường thẳng này cắt AB và AC lần lượt tại D và E. Chứng minh rằng:
a) Tam giác ADE cân
b) BD=CE
. Cho tam giác ABC cân ở A , trên cạnh AB và AC lần lượt lấy hai điểm E và D sao cho AD= AE ; BD cắt CE tại G . Chứng minh rằng:
a) BD =CE;
b) tam giác GDE cân;
c) Gọi M là trung điểm của BC . Chứng minh ba điểm A ,G ,M thẳng hàng.
d) Cho AB=13 cm, MB=5 cm . Tính độ dài đoạn AM
a: Xét ΔBEC và ΔCDB có
BE=CD
\(\widehat{EBC}=\widehat{DCB}\)
BC chung
Do đó: ΔBEC=ΔCDB
Suy ra: CE=DB
b: Xét ΔGBC có \(\widehat{GCB}=\widehat{GBC}\)
nên ΔGBC cân tại G
=>GB=GC
Ta có: GB+GD=BD
GE+GC=CE
mà BD=CE
và GB=GC
nên GD=GE
hay ΔGDE cân tại G
c: Ta có: AB=AC
nên A nằm trên đường trung trực của BC(1)
Ta có: GB=GC
nên G nằm trên đường trung trực của BC(2)
Ta có: MB=MC
nên M nằm trên đường trung trực của BC(3)
Từ (1), (2) và (3) suy ra A,G,M thẳng hàng
Đúng 2
Bình luận (0)



















