Nếu sinx+cosx=1/2 thì sinx, cosx Bằng

Những câu hỏi liên quan
Nếu sinx + cosx = 1/2 thì 3sinx + 2cosx bằng
![]()
![]()
![]()
![]()
Chọn A.
Ta có:
sinx + cosx = ½ nên ( sinx + cosx)2 = ¼
Do đó sinx. cosx = -3/8
Khi đó sinx; cosx là nghiệm của phương trình
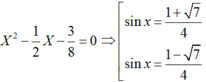
Ta có sinx + cos x = ½ nên 2( sinx + cosx) = 1
+) Với 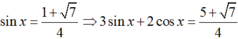
+) Với 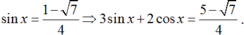
Đúng 0
Bình luận (0)
Nếu sinx + cosx 1/2 thì 3sinx + 2cosx bằng
Đọc tiếp
Nếu sinx + cosx= 1/2 thì 3sinx + 2cosx bằng
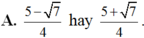
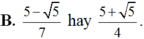
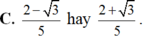
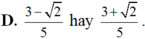
Chọn A.
Từ giả thiết ta suy ra: (sinx+ cosx) 2 = ¼
Suy ra: 2sinx.cosx = -3/4 hay sinx.cosx = -3/8
Khi đó sinx; cosx là nghiệm của phương trình
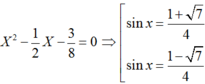
Do sinx + cosx = ½ nên 2(sinx + cosx) = 1
+) Với 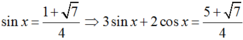
+) Với 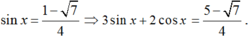
Đúng 0
Bình luận (0)
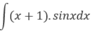 bằng:
bằng:
A. (x + 1)cosx + sinx + C B. -(x + 1)cosx + sinx + C
C. -(x + 1)sinx + cosx + C D. (x + 1)cosx - sinx + C
Đáp án: B.
Hướng dẫn: Đặt u = (x + 1), v' = sinx.
Đúng 0
Bình luận (0)
∫
x
+
1
.
s
i
n
x
d
x
bằng:A. (x + 1)cosx + sinx + C B. -(x + 1)cosx + sinx + CC. -(x + 1)sinx + cosx + C D. (x + 1)cosx - sinx + C
Đọc tiếp
∫ x + 1 . s i n x d x bằng:
A. (x + 1)cosx + sinx + C B. -(x + 1)cosx + sinx + C
C. -(x + 1)sinx + cosx + C D. (x + 1)cosx - sinx + C
Đáp án: B.
Hướng dẫn: Đặt u = (x + 1), v' = sinx.
Đúng 0
Bình luận (0)
Cmr:
1) (Sinx)/(1+cosx)+(1+cosx)/sinx=2/sinx
2) cosx/(1-sinx)=cot(bi/4-x/2)
\(\frac{sinx}{1+cosx}+\frac{1+cosx}{sinx}=\frac{sin^2x+\left(1+cosx\right)^2}{sinx\left(1+cosx\right)}=\frac{sin^2x+cos^2x+2cosx+1}{sinx\left(1+cosx\right)}\)
\(=\frac{2+2cosx}{sinx\left(1+cosx\right)}=\frac{2\left(1+cosx\right)}{sinx\left(1+cosx\right)}=\frac{2}{sinx}\)
\(\frac{cosx}{1-sinx}=\frac{cos2.\frac{x}{2}}{1-sin2.\frac{x}{2}}=\frac{cos^2\frac{x}{2}-sin^2\frac{x}{2}}{sin^2\frac{x}{2}+cos^2\frac{x}{2}-2sin\frac{x}{2}.cos\frac{x}{2}}=\frac{\left(cos\frac{x}{2}-sin\frac{x}{2}\right)\left(cos\frac{x}{2}+sin\frac{x}{2}\right)}{\left(cos\frac{x}{2}-sin\frac{x}{2}\right)^2}\)
\(=\frac{sin\frac{x}{2}+cos\frac{x}{2}}{cos\frac{x}{2}-sin\frac{x}{2}}=\frac{\sqrt{2}cos\left(\frac{\pi}{4}-\frac{x}{2}\right)}{\sqrt{2}sin\left(\frac{\pi}{4}-\frac{x}{2}\right)}=cot\left(\frac{\pi}{4}-\frac{x}{2}\right)\)
Đúng 1
Bình luận (0)
Nếu
sin
x
+
cos
x
1
2
thì
sin
2
x
bằng A.
3
4
B.
3
8
C.
2
2
D.
-
3
4
Đọc tiếp
Nếu sin x + cos x = 1 2 thì sin 2 x bằng
A. 3 4
B. 3 8
C. 2 2
D. - 3 4
2/sinx- sinx/1+ cosx=1+cosx/sinx
\(\frac{2}{sinx}-\frac{sinx}{1+cosx}=\frac{2\left(1+cosx\right)-sin^2x}{sinx\left(1+cosx\right)}=\frac{2+2cosx-sin^2x}{sinx\left(1+cosx\right)}\)
\(=\frac{\left(1-sin^2x\right)+2cosx+1}{sinx\left(1+cosx\right)}=\frac{cos^2x+2cosx+1}{sinx\left(1+cosx\right)}=\frac{\left(cosx+1\right)^2}{sinx\left(1+cosx\right)}=\frac{1+cosx}{sinx}\)
Đúng 0
Bình luận (0)
Giải phương trình:
1,\(sin^3x+cos^3x=1-\dfrac{1}{2}sin2x\)
2,\(|cosx-sinx|+2sin2x=1\)
3,\(2sin2x-3\sqrt{6}|sinx+cosx|+8=0\)
4,\(cosx+\dfrac{1}{cosx}+sinx+\dfrac{1}{sinx}=\dfrac{10}{3}\)
1.
\(sin^3x+cos^3x=1-\dfrac{1}{2}sin2x\)
\(\Leftrightarrow\left(sinx+cosx\right)\left(sin^2x+cos^2x-sinx.cosx\right)=1-sinx.cosx\)
\(\Leftrightarrow\left(sinx+cosx\right)\left(1-sinx.cosx\right)=1-sinx.cosx\)
\(\Leftrightarrow\left(1-sinx.cosx\right)\left(sinx+cosx-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sinx.cosx=1\\sinx+cosx=1\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}sin2x=2\left(vn\right)\\\sqrt{2}sin\left(x+\dfrac{\pi}{4}\right)=1\end{matrix}\right.\)
\(\Leftrightarrow sin\left(x+\dfrac{\pi}{4}\right)=\dfrac{1}{\sqrt{2}}\)
\(\Leftrightarrow\left[{}\begin{matrix}x+\dfrac{\pi}{4}=\dfrac{\pi}{4}+k2\pi\\x+\dfrac{\pi}{4}=\pi-\dfrac{\pi}{4}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=k2\pi\\x=\dfrac{\pi}{2}+k2\pi\end{matrix}\right.\)
Đúng 1
Bình luận (0)
2.
\(\left|cosx-sinx\right|+2sin2x=1\)
\(\Leftrightarrow\left|cosx-sinx\right|-1+2sin2x=0\)
\(\Leftrightarrow\left|cosx-sinx\right|-\left(cosx-sinx\right)^2=0\)
\(\Leftrightarrow\left|cosx-sinx\right|\left(1-\left|cosx-sinx\right|\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sin\left(x-\dfrac{\pi}{4}\right)=0\\\left|cosx-sinx\right|=1\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x-\dfrac{\pi}{4}=k\pi\\cos^2x+sin^2x-2sinx.cosx=1\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{4}+k\pi\\1-sin2x=1\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{4}+k\pi\\sin2x=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{4}+k\pi\\x=\dfrac{k\pi}{2}\end{matrix}\right.\)
Đúng 1
Bình luận (0)
3.
\(2sin2x-3\sqrt{6}\left|sinx+cosx\right|+8=0\)
\(\Leftrightarrow2\left(sinx+cosx\right)^2-3\sqrt{6}\left|sinx+cosx\right|+6=0\)
\(\Leftrightarrow\left[{}\begin{matrix}\left|sinx+cosx\right|=\sqrt{6}\left(vn\right)\\\left|sinx+cosx\right|=\dfrac{\sqrt{6}}{2}\end{matrix}\right.\)
\(\Leftrightarrow\left|sin\left(x+\dfrac{\pi}{4}\right)\right|=\dfrac{\sqrt{3}}{2}\)
\(\Leftrightarrow sin\left(x+\dfrac{\pi}{4}\right)=\pm\dfrac{\sqrt{3}}{2}\)
...
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
chứng minh: cosx/sinx-cosx + sinx/sinx+cosx=1+cot2x/1-cot2x











