Hai đường tròn tiếp xúc trong tại A.Dây cung CD của đường tròn lớn tiếp xúc với đường nhỏ tại P. CM: AP là phan giác CAD
Những câu hỏi liên quan
Bài 1: Cho tam giác nhọn ABC nội tiếp đường tròn (O). Đường tròn (I) qua A và tiếp xúc với BC tại B. Đường tròn (K) qua A và tiếp xúc với BC tại C. Các đường tròn (I) và(K) cắt tại M. Đường thẳng AM cắt đường tròn (O) tại N. C/m: BMCN là hình bình hànhBài 2: Cho tam giác đều ABC nội tiếp đường tròn (O). Trên cung nhỏ BC lấy điểm M và vẽ đường tròn (I) tiếp xúc trong với (O) tại M. Gọi giao điểm MA, MB, MC với (I) theo tứ tự D,E,F a) C/m: tam giác DEF đều. b) Từ A,B,C vẽ các tiếp tuyến với đư...
Đọc tiếp
Bài 1: Cho tam giác nhọn ABC nội tiếp đường tròn (O). Đường tròn (I) qua A và tiếp xúc với BC tại B. Đường tròn (K) qua A và tiếp xúc với BC tại C. Các đường tròn (I) và(K) cắt tại M. Đường thẳng AM cắt đường tròn (O) tại N. C/m: BMCN là hình bình hành
Bài 2: Cho tam giác đều ABC nội tiếp đường tròn (O). Trên cung nhỏ BC lấy điểm M và vẽ đường tròn (I) tiếp xúc trong với (O) tại M. Gọi giao điểm MA, MB, MC với (I) theo tứ tự D,E,F
a) C/m: tam giác DEF đều.
b) Từ A,B,C vẽ các tiếp tuyến với đường tròn (I) lần lượt là AP,BQ,CR( P,Q,R là tiếp điểm). C/m: AP=PQ+CR
Cho đường tròn (I) tiếp xúc trong với đường tròn (O) tại A . Đường kính AB của đường tròn (O) cắt đường tròn (I) tại điểm thứ hai C khác A . Từ B vẽ tiếp tuyến BP với đường tròn (I) cắt đường tròn (O) tại Q .Chứng minh AP là phân giác của góc IAQ
cho hai đường tròn (O) và (O') cắt nhau tại A và B .Dây AC của đường tròn (O) tiếp xúc với đường tròn (O') tại A.Dây AD của đường tròn (O') tiếp xúc với đường tròn (O) tại A.Gọi K là điểm đối xứng với A qua trung điểm I của OO' ,E là điểm đối xứng với A và B.cmr:
a)AB vuông góc với KB
b)Bốn điểm A,C,E,D nằm trên cùng một đường tròn
Cho hai đường tròn (O) và (O’) tiếp xúc ngoài tại A. Gọi CD là tiếp tuyến chung ngoài của hai đường tròn (C ∈ (O), D ∈ (O’)). Tính số đo góc CAD
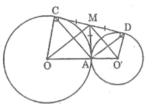
Kẻ tiếp tuyến chung tạ IA cắt CD tại M
Trong đường tròn (O) ta có:
MA = MC (tính chất hai tiếp tuyến cắt nhau)
Trong đường tròn (O’) ta có :
MA = MD (tính chất hai tiếp tuyến cắt nhau)
Suy ra : MA = MC = MD = 12 CD
Tam giác ACD có đường trung tuyến AM ứng với cạnh CD bằng nửa cạnh CD nên tam giác ACD vuông tại A
Suy ra : 
Đúng 0
Bình luận (0)
Cho đường tròn (O, 5 cm), dây CD= 8cm. Vẽ đường thẳng xy song song với CD và tiếp xúc với đường tròn O tại A nằm trên cung nhỏ CD . Khoảng cách giữa xy và CD là.... cm
viết đáp án là được nka
Cho hai đường tròn đồng tâm. Trong đường tròn lớn vẽ hai dây bằng nhau AB = CD và cùng tiếp xúc với đường tròn nhỏ tại M và N sao cho AB vuông góc với CD tại I. Tính bán kính đường tròn nhỏ biết IA = 3cm và IB = 9cm.
Cho tam giác ABC nội tiếp đường tròn (O). Đường phân giác AD của tam giác ABC cắt cung BC ở E. Đường tròn (I) tiếp xúc trong với (O) và tiếp xúc với BC tại T cắt AD ở M, N (N nằm giữa A và M); CM cắt đường tròn (O) tại K. Vẽ dây KL//AB. Chứng minh rằng ba điểm C, N, L thẳng hàng.
CM được S,T,E thẳng hàng
Xét tam giác ECT zà tam giác EST có \(\widehat{CET}\left(chung\right),\widehat{ECT}=\widehat{ESC}\)
=>tam giác ECT=tam giác EST(g.g)
=>\(\frac{EC}{ES}=\frac{ET}{EC}=>ET.ES=EC^2\)
xét tam giác EMT zà tam giác ESN có \(\widehat{MET}\left(chung\right),\widehat{EMT}=\widehat{ESN}\)
=> tam giác ECT = tam giác ESN(g.g)
=>\(\frac{EM}{ES}=\frac{ET}{EN}=>ET.ES=EM.EN=EM.EN\\\)
Nên \(EC^2=EM.EN=\left(=ET.ES\right)=\frac{EC}{EN}=\frac{EM}{EC}\)
tam giác ECM = tam giasc ENC (c.g.c)
=>\(\widehat{EMC}=\widehat{ENC}\)
=>\(\widehat{ECD}+\widehat{DCM}=\widehat{NAC}+\widehat{NCA}\)
mà \(\widehat{ECD=\widehat{NAC}}\)
nên \(\widehat{DCM}=\widehat{NCA}\)
ta có \(KL//AB=>\widebat{BK}=\widebat{AL}=>\widehat{DCM}=\widehat{LCA}\)
ta có\(\widehat{NCA}=\widehat{LCA}\left(=\widehat{DCM}\right)\)
=> hai tia CN , CL trùng nhau .zậy C,N,L thẳng hàng
Cho dường tròn ( O' ) tiếp xúc với đường tròn ( O ) tại A . Dây BC của đường tròn lớn tiếp xúc với đường tròn nhỏ tại H. Gọi D , E theo thứ tự là giao điểm ( khác A ) của AB , AC với dường tròn nhỏ . Chứng minh :
a) DE song song BC
b) AH là tia phân giác góc BAC .
Bài 1: Cho đường tròn (O1) tiếp xúc trong với đường tròn (O) tại A . Đường kính AB của đường tròn (O) cắt đường tròn (O1) tại điểm thứ hai C khác A . Từ B vẽ tiếp tuyến BP với đường tròn (O1) cắt đường tròn (O) tại Q .Chứng minh AP là phân giác của góc QAB.
Mấy bro giúp mình với T^T