Tồn tại 2 số phức khác nhau có modul bằng nhau và phần thực bằng nhau. Là số nào?

Những câu hỏi liên quan
Cho a,b,c là 3 số phức phân biệt khác 0 và modul của chúng bằng nhau .Nếu một nghiệm của phương trình az2 + bz + c = 0 có môđun bằng 1 thì khẳng định nào sau đây đúng.
A. c2 = ab
B. a2 = bc
C. b = ac
D. b2 = ac
Chọn D.
Giả sử z1; z2 là nghiệm của phương trình đã cho với |z| = 1.
Theo định lý Viet ta có 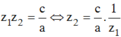 .Suy ra
.Suy ra 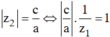
Bởi vì 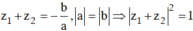 , suy ra
, suy ra ![]()
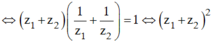
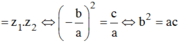
Đúng 0
Bình luận (0)
Cho số phức z cóphần thực bằng 2 và phần ảo bằng -3.Modul của số phức 3+iz là A.. B. . C. D..
Đọc tiếp
Cho số phức z cóphần thực bằng 2 và phần ảo bằng -3.Modul của số phức 3+iz là
A.![]() .
.
B. ![]() .
.
C. ![]()
D.![]() .
.
Gọi
z
1
,
z
2
là 2 số phức có phần thực bằng nhau và
z
1
z
2
thì
A
.
z
1
z
2
B
.
z
1...
Đọc tiếp
Gọi z 1 , z 2 là 2 số phức có phần thực bằng nhau và z 1 = z 2 thì
A . z 1 = z 2
B . z 1 = - z 2
C . z 1 = z 2 h o ặ c z 1 ¯ = z 2
D . z 1 = - z 2 ¯
Có tồn tại hai số dương a và b khác nhau sao cho 1 phần a - 1 phần b bằng 1 phần a-b
Biết tập hợp điểm M biểu diễn số phức z là đường thẳng (d): 3x + 2y – 5 = 0. Tìm số phức z sao cho phần thực và phần ảo bằng nhau
A. z = 5 + 5i
B. z = 5 – 5i
C. z = -5 + 5i
D. z = 1 + i
cho 51 số tự nhiên khác o và khác nhau không quá 100 . Chứng minh rằng tồn tại 2 trong số 51 số đó có tổng bằng 101
Cho 51 số tự nhiên khác 0 và khác nhau không quá 100. Chứng minh rằng tồn tại 2 trong 51 số ấy có tổng bằng 101
Gọi 51 số đó là a1;a2;a3;...;a50;a51
Không làm mất tính tổng quát, ta giả sử \(a_1< a_2< a_3< ...< a_{51}\)(nhóm số 1 có 51 số)
Xét nhóm số thứ 2 có 51 hiệu: \(100-a_1>100-a_2>100-a_3>...>100-a_{51}\)
Tổng cộng 2 nhóm có 102 số mà 102 số này không quá 100 và khác 0 nên chúng nhận các giá trị 1;2;3;...;100 có 100 giá trị. Vậy theo nguyên lí Đi-rích-lê thì có [102/100]+1=2 số nhận cùng 1 giá trị. Mà hai số này hiển nhiên không thuộc cùng 1 nhóm nên nó sẽ thuộc hai nhóm khác nhau. Gọi chúng là 101-\(a_m\)=\(a_n\) suy ra 100=\(a_m+a_n\)hay ta có đpcm
Đúng 0
Bình luận (0)
Sửa khúc cuối nhé!: Gọi hai số đó là \(a_n;101-a_m\left(1\le m;n\le51\right)\Rightarrow a_n=101-a_m\)hay \(a_m+a_n=101\)vậy ta có đpcm
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
a) số thập phân nhỏ nhất có 4 chữ số khác nhau ở cả phần nguyên và phần thập phân mà chữ số hàng trăm bằng 2 là:
b) số thập phân lớn nhất có 4 chữ số khác nhau ở cả phần nguyên và phần thập phân viết được từ 5 số 0,1,3,5,7, là:
c) số thập phân nhỏ nhất có 5 chữ số khác nhau ở cả phần nguyên và phần thập phân mà chữ số phần mười của nó bằng 0 là:
Cho 53 số nguyên dương khác nhau có tổng bằng 1998. Chứng minh rằng trong 53 số nguyên đã cho bao giờ cũng tồn tại 2 số có tổng bằng 53













