Giải:

Dùng biến đổi tương đương chứng minh được:

\(\left(x^2+x+2\right)^2=x^4+5x^3+4x+4>x^4+2x^3+2x^2+x+3>\) \(x^4+2x^3+x^2=\left(x^2+x\right)^2\)

\(\Rightarrow x^4+2x^3+2x^2+x+3=\left(x^2+x+1\right)^2\)

\(\Leftrightarrow x^4+2x^3+2x^2+x+3=x^4+2x^3+3x^2+2x+1\)

\(\Leftrightarrow x^2+x-2=0\Leftrightarrow\orbr{\begin{cases}x=1\\x=-2\end{cases}}\)

Vậy \(x=1\) hoặc \(x=-2\) thì phương trình trên là số chính phương

dùng phương pháp hệ số bất định ý bạn gọi đa thức đó là bình phương của đa thức (x^2+ax+b)^2 rồi khai triển là ok

Đặt: \(y^2=\) \(x^4+\left(x+1\right)^3-2x^2-2x\)

= \(x^4+x^3+x^2+x+1\) là số chính phương 

<=> \(4y^2=4x^4+4x^3+4x^2+4x+4\)

Ta có: 

\(4y^2=4x^4+4x^3+4x^2+4x+4>4x^4+4x^3+x^2=\left(2x^2+x\right)^2\)

\(4y^2=4x^4+4x^3+4x^2+4x+4\le4x^4+4x^3+9x^2+4x+4=\left(2x^2+x+2\right)^2\)

=> \(\left(2x^2+x\right)^2< \left(2y\right)^2\le\left(2x^2+x+2\right)^2\)

=> \(\orbr{\begin{cases}4y^2=\left(2x^2+x+2\right)^2\\4y^2=\left(2x^2+x+1\right)^2\end{cases}}\)

TH1: \(4y^2=\left(2x^2+x+2\right)^2\)

hay \(4x^4+4x^3+4x^2+4x+4=4x^4+4x^3+9x^2+4x+4\)

<=> \(x=0\)thỏa mãn

Th2: \(4y^2=\left(2x^2+x+1\right)^2\)

hay \(4x^4+4x^3+4x^2+4x+4=4x^4+5x^2+1+4x^3+2x\)

<=> \(x^2-2x-3=0\)

<=> x = 3 hoặc x = -1. thử lại thỏa mãn 

Vậy x = 0 ; x = -1 hoặc x = 3

a. \(x=\left\{4;9;16\right\}\)

b. \(x=1\)

c. \(x=\left\{-2;-1\right\}\)

Mode 5 3 trên máy tính Casio fx-570 :

a) a=1,b=-2,c=-4

b) a=1,b=-2,c=7 

MK ko biế đúng ko nữa , sai thì ý kiến

a)

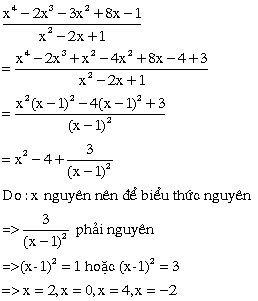
b)

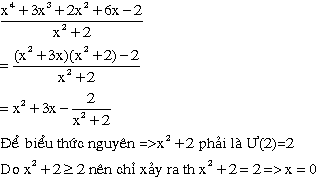
Chúc các bn hok tốt

Tham khảo nhé

Dây là 4 số  nguyên dương liên tiếp, còn phần  kia tương tự nha

Đặt A = n.(n+1)(n+2)(n+3) với n ≥ 1; n € N 
A = [n.(n+3)].[(n+1)(n+2)] = (n² + 3n).(n²+3n+2) 
= t(t+2) (với t = n² + 3n ≥ 4 ; t € N) 
Ta thấy 
t² < A = t² + 2t < t² + 2t + 1 = (t+1)² 
=> A nằm giữa 2 số chính phương liên tiếp 
=> A không phải là số chính phương (đpcm)

bạn ơi, mấy bn hok giỏi ko onl ùi

chắc tại mưa nên mấy bn ấy k onl

2/ 

a) \(\frac{1}{x}+\frac{1}{y}=\frac{1}{3}\) (\(x,y\ne0;x,y\ge1\))

Vai trò của x và y là bình đẳng,giả sử \(x\ge y\ge1\)

Hiển nhiên,ta có: \(\frac{1}{y}< \frac{1}{3}\Rightarrow y>3\).Mà y nguyên nên \(y\ge4\)

Mặt khác, do \(x\ge y\ge1\)nên \(\frac{1}{x}\le\frac{1}{y}\).Do vậy:

\(\frac{1}{3}=\frac{1}{x}+\frac{1}{y}\le\frac{1}{y}+\frac{1}{y}=\frac{2}{y}\)

\(\Rightarrow\frac{2}{y}\ge\frac{1}{3}\Rightarrow y\le6\)

Từ đó,ta xác định được khoảng giá trị của y là: \(4\le y\le6\)

+Với y = 4 suy ra x = 12

+Với y = 5 suy ra x = 2/15 (loại,vì x không là số nguyên)

+Với y = 6 suy ra x = 6

Vậy các nghiệm của phương trình: (4;12), (12;4), (6,6)