Chứng minh rằng các bất phương trình sau có nghiệm là mọi số thực x
2x2-2x+1>0
Những câu hỏi liên quan
Cho phương trình: x² - mx + m - 1 = 0(x là ẩn) a) Chứng minh rằng phương trình luôn có nghiệm với mọi giá trị của m b) Tìm giá trị của m để phương trình có 2 nghiệm x1, x2 thoả mãn: x1 - 2x2 = 1
cho 2 phương trình bậc hai x2 - 2x + m = 0 (1)
(1) Tìm m để phương trình (1) có nghiệm
(2) Chứng minh rằng với mọi m, phương trình (1) không thể có hai nghiệm cùng là số âm
(3) Tìm m để phương trình (1) có hai nghiệm thỏa mãn x1 - 2x2 =5
(1) Phương trình 1 có nghiệm
<=> \(\Delta'\ge0\)<=> \(1-m\ge0\Leftrightarrow m\le1\)
(2) Gọi x1 , x2 là 2 nghiệm của phương trình
x1+x2=2>0 => Phương trình có ít nhất một nghiệm dương => Không thẻ có 2 nghiệm cùng là số âm
(3) x1+x2=2, x1-2x2=5
=> x1=3, x2=-1
mà x1.x2=m => m=-3
Đúng 1
Bình luận (0)
em vẫn thắc mắc câu (3) ạ, chị giải thích rõ cho em với
Đúng 0
Bình luận (0)
Theo đề vài X1 -2. x2 =5 (1)
Theo định lí Viet
x1 +x2=2 (2)
x1. x2=m (3)
Từ (1) (2) Suy ra x1=3, x2=-1
Thay vào (3) suy ra m=-3
Đúng 0
Bình luận (0)
Tìm tất cả các giá trị thực của tham số m sao cho bất phương trình
(
1
+
2
x
)
(
3
-
m
)
m
+
2
x
2
-
5
x
-
3
nghiệm đúng với mọ...
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m sao cho bất phương trình ( 1 + 2 x ) ( 3 - m ) > m + 2 x 2 - 5 x - 3 nghiệm đúng với mọi x ∈ - 1 2 ; 3 ?
A. m > 1 .
B. m>0.
C. m<1.
D. m<0.
Cho bất phương trình
x
4
+
x
2
+
m
3
-
2
x
2
+
1
3
+
x
2
x
2...
Đọc tiếp
Cho bất phương trình x 4 + x 2 + m 3 - 2 x 2 + 1 3 + x 2 x 2 - 1 > 1 - m (m là tham số). Tìm tất cả các giá trị thực của tham số m để bất phương trình nghiệm đúng với mọi x > 1
A. m > 1
B. m ≥ 1
C. m > 5 4
D. m ≥ 5 4
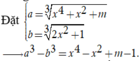
Khi đó bất phương trình trở thành
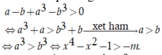
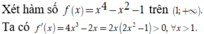
Suy ra hàm số f(x) đồng biến trên 
Do đó yêu cầu bài toán 
Chọn B.
Đúng 0
Bình luận (0)
Cho hàm số
f
x
2
x
-
2
-
x
. Có bao nhiêu số nguyên m để bất phương trình
f
x
3
-
2
x
2
+
3
x...
Đọc tiếp
Cho hàm số f x = 2 x - 2 - x . Có bao nhiêu số nguyên m để bất phương trình f x 3 - 2 x 2 + 3 x - m + f 2 x - 2 x 2 - 5 < 0 có nghiệm đúng với mọi x ∈ 0 ; 1 .
A. 7.
B. 3.
C. 9.
D. 5.
chứng minh rằng bất phương trình sau nghiệm đúng với mọi x: \(\frac{-4}{x^2-2x+2}\)-5<0
Ta có \(x^2-2x+2=\left(x-1\right)^2+1>0\)
\(\Rightarrow\frac{-4}{x^2-2x+2}< 0\)
\(\Rightarrow\frac{-4}{x^2-2x+2}-5< 0\)(đúng vóiư mọi x)
chứng minh mọi số thực là x đều là nghiệm của bất phương trình sau
\(2x^2-4x+5>0\)
mong ai đó giúp mình với
\(2x^2-4x+5=2x^2-4x+2+3=2\left(x-1\right)^2+3>0\)
ta có điều phải chứng minh
Với m là tham số thực dương khác 1. Hãy tìm tập nghiêm S của bất phương trình logm(2x2 + x + 3)
≤
logm(3x2 - x). Biết rằng x 1 là một nghiệm của bất phương trình.
Đọc tiếp
Với m là tham số thực dương khác 1. Hãy tìm tập nghiêm S của bất phương trình logm(2x2 + x + 3) ≤ logm(3x2 - x). Biết rằng x = 1 là một nghiệm của bất phương trình.
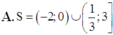
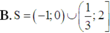
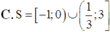
Đáp án C
Vì x = 1 là một nghiệm của bất phương trình
Khi đó, bất phương trình
Đúng 0
Bình luận (0)
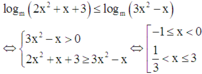
CM các bất phương trình sau luôn dương vs mọi x
1)2x2-2x+17>0
2)-x2+6x-18<0
3)|x-1|+|x|+2>1
BPT thì làm sao gọi là luôn dương hả bạn? Đề phải là CMR các BPT sau luôn đúng với mọi $x$.
1.
Ta có: $2x^2-2x+17=x^2+(x^2-2x+1)+16=x^2+(x-1)^2+16\geq 16>0$ với mọi $x\in\mathbb{R}$
Do đó BPT luôn đúng với mọi $x$
2.
$-x^2+6x-18=-(x^2-6x+18)=-[(x^2-6x+9)+9]=-[(x-3)^2+9]$
$=-9-(x-3)^2\leq -9<0$ với mọi $x\in\mathbb{R}$
Vậy BPT luôn đúng với mọi $x$
3.
$|x-1|+|x|+2\geq 0+0+2=2>1$ với mọi $x\in\mathbb{R}$
Do đó BPT luôn đúng với mọi $x$
Đúng 0
Bình luận (0)