Phát biểu định nghĩa đường trung tuyến của tam giác vẽ hình và ghi giả thiết kết luận

Những câu hỏi liên quan
Phát biểu định nghĩa tính chất 3 đường trung tuyến của tam giác vẽ hình và ghi giả thuyết kết luận
Tính chất ba đường trung tuyến của tam giác
Định lý: Ba đương trung tuyến của tam giác cùng đi qua điểm. điểm đó cách đỉnh một khoảng bằng 2/3 độ dài đường trung tuyến đi qua đỉnh ấy.
Giao điểm của ba đường trung tuyến gọi là trọng tâm
GT : G là trọng tâm ∆ ABC
KL : AG/AD = BG/BE = CG/CF = 2/3
Đúng 2
Bình luận (2)
TK:https://loigiaihay.com/ly-thuyet-tinh-chat-ba-duong-trung-tuyen-cua-tam-giac-c42a5574.html
Đúng 0
Bình luận (0)
1. Phát biểu, vẽ hình, ghi giả thiết - kết luận của định lí Ta-let, định lí đảo, hệ quả
2. Phát biểu, vẽ hình, ghi giả thiết - kết luận của tính chất đường phân giác trong tam giác
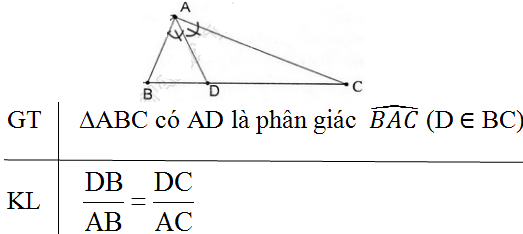
Phát biểu định lí về tính chất của đường phân giác trong tam giác (vẽ hình, ghi giả thiết và kết luận).
Định lý:
Trong tam giác, đường phân giác của một góc chia cạnh đối diện thành hai đoạn thẳng tỉ lệ với hai cạnh kề của hai đoạn ấy.
Đúng 0
Bình luận (0)
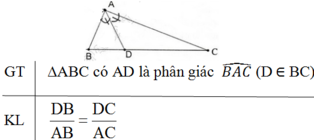
Phát biểu định lí về tính chất của đường phân giác trong tam giác (vẽ hình, ghi giả thiết và kết luận) ?
Định lý:
Trong tam giác, đường phân giác của một góc chia cạnh đối diện thành hai đoạn thẳng tỉ lệ với hai cạnh kề của hai đoạn ấy.
Đúng 0
Bình luận (0)
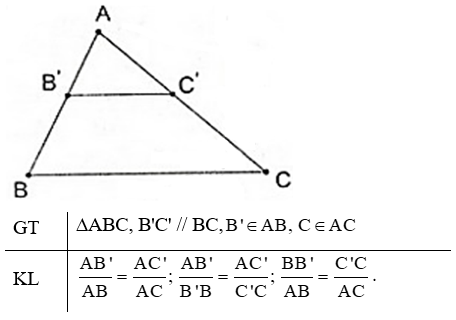
Phát biểu, vẽ hình, ghi giả thiết và kết luận của định lí Talet trong tam giác.
Định lí Talet trong tam giác:
Nếu một đường thẳng song song với một cạnh của một tam giác và cắt hai cạnh còn lại thì nó định ra trên hai cạnh ấy những đoạn thẳng tương ứng tỉ lệ.
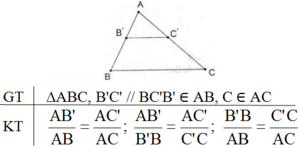
Đúng 0
Bình luận (0)
Phát biểu, vẽ hình, ghi giả thiết và kết luận của định lí Ta - lét trong tam giác ?
Định lí Talet trong tam giác:
Nếu một đường thẳng song song với một cạnh của một tam giác và cắt hai cạnh còn lại thì nó định ra trên hai cạnh ấy những đoạn thẳng tương ứng tỉ lệ.
Đúng 1
Bình luận (0)
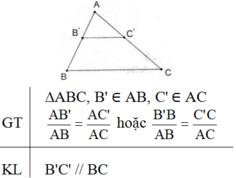
Phát biểu, vẽ hình, ghi giả thiết và kết luận của định lí Talet đảo.
Định lí Talet đảo:
Nếu một đường thẳng cắt hai cạnh của một tam giác và định ra trên hai cạnh ấy những đoạn thẳng tương ứng tỉ lệ thì đường thẳng đó song song với cạnh còn lại của tam giác.
Đúng 0
Bình luận (0)
1) Nêu định nghĩa và tính chất của hai góc đối đỉnh? Vẽ hình? Ghi giả thiết, kết luận.
2) Phát biểu định nghĩa đường trung trực của đoạn thẳng? Vẽ hình minh họa.
3) Phát biểu dấu hiệu nhận biết hai đường thẳng song song? Vẽ hình ghi giả thiết, kết luận.
4) Phát biểu tiên đề ơclit? Vẽ hình minh họa.
5) Phát biểu định lí về tổng 3 góc của một tam giác? Định nghĩa và tính chất góc ngoài của tam giác.
6) Phát biểu các trường hợp bằng nhau của hai tam giác? Vẽ hình ghi giả thiết, kết luận.
Đọc tiếp
1) Nêu định nghĩa và tính chất của hai góc đối đỉnh? Vẽ hình? Ghi giả thiết, kết luận.
2) Phát biểu định nghĩa đường trung trực của đoạn thẳng? Vẽ hình minh họa.
3) Phát biểu dấu hiệu nhận biết hai đường thẳng song song? Vẽ hình ghi giả thiết, kết luận.
4) Phát biểu tiên đề ơclit? Vẽ hình minh họa.
5) Phát biểu định lí về tổng 3 góc của một tam giác? Định nghĩa và tính chất góc ngoài của tam giác.
6) Phát biểu các trường hợp bằng nhau của hai tam giác? Vẽ hình ghi giả thiết, kết luận.
1)
Lý thuyết về hai góc đối đỉnh.
Kiến thức cơ bản:
1. Hai góc đối đỉnh:
Hai góc đối đỉnh là hai góc mà mối cạnh của góc này là tia đối của một cạnh của góc kia.
2. Tính chất:
Hai góc đối đỉnh thì bằng nhau
VD: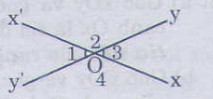
ˆO1O1^ đối đỉnh với ˆO3⇒ˆO1=ˆO3O3^⇒O1^=O3^
ˆO2O2^ đối đỉnh với ˆO4⇒ˆO2=ˆO4
ĐỊNH LÝ:
Hai góc đối đỉnh thì bằng nhau
Hai góc đối đỉnh là 2 góc có cạnh của góc này là tia đối của cạnh góc kia
Đúng 1
Bình luận (2)
2)
A. KIẾN THỨC CƠ BẢN
1. Định nghĩa đường trung trực của một đoạn thẳng
Đường thẳng đi qua trung điểm của đoạn thẳng và vuông góc với đoạn thẳng gọi là đường trung trực của đoạn thẳng ấy
d là đường trung trực của đoạn thẳng AB
2. Định lí 1:
Điểm nằm trên đường trung trực của một đoạn thẳng thì cách đều hai mút của đoạn thẳng đó
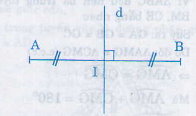
GT : d là trung trực của AB
M ∈ d
KL : MA = MB
Định lí 2:
Điểm cách đều hai mút của một đoạn thẳng thì nằm trên đường trung trực của đoạn thẳng đó

3. Nhận xét
Từ định lí thuận và đảo ta có:
Tập hợp các điểm cách đều hai mút của một đoạn thẳng là đường trung trực của đoạn thẳng đó.
Đúng 0
Bình luận (2)
3)
Lý thuyết về hai đường thẳng song song.
Tóm tắt kiến thức:
1. Khái niệm

- Hai đường thẳng song song là hai đường thẳng không có điểm chung. Ký hiệu a//b.
- Hai đường thẳng phân biệt thì hoặc cắt nhau hoặc song song.
2. Dấu hiệu nhận biết hai đường thẳng song song
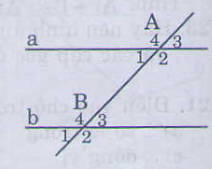
Nếu đường thẳng c cắt hai đường thẳng a, b và trong các góc tạo thành có một cặp góc so le trong bằng nhau (hoặc cặp góc đồng vị bằng nhau) thì a và b song song với nhau.
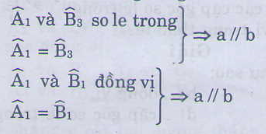
giả thiết kết luận thì..............sorry nha
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
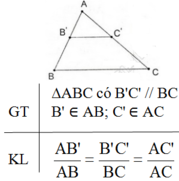
Phát biểu, vẽ hình, ghi giả thiết và kết luận về hệ quả của định lí Talet.
Hệ quả của định lí Talet:
Nếu một đường thẳng cắt hai cạnh của một tam giác và song song với cạnh còn lại thì nó tạo thành một tam giác mới có ba cạnh tương ứng với tỉ lệ ba cạnh của tam giác đã cho.
Đúng 0
Bình luận (0)