vẽ đồ thị hàm số
a) y = |x| - 2
b) y = |2x + 1|

Những câu hỏi liên quan
vẽ đồ thị các hàm số
a. y = x + 2
b. y = -1/2 x + 1
Lập bảng biến thiên và vẽ đồ thị hàm số
a) y = |x-1|+|2x-4|
b) y = \(\left\{{}\begin{matrix}2x-1,x\ge1\\-x+2,x< 1\end{matrix}\right.\)
Vẽ trên cũng một hệ trục tọa độ Oxy đồ thị của các hàm số
a) y = x b) y=3x
c) y = -2x d) Y = -x
Bài 1. Cho hàm số y 2x-1a) Tính giá trị của hàm số y khi x0; x1; x -2b) Tìm giá trị của x khi y3Bài 2. Cho hàm số y -3xa) Vẽ đồ thị hàm sốb) Tìm trên đồ thị hàm số điểm có hoành độ bằng 2c) Tìm trên đồ thị hàm số điểm có tung độ bằng -6
Đọc tiếp
Bài 1. Cho hàm số
y= 2x-1
a) Tính giá trị của hàm số y khi x=0; x=1; x= -2
b) Tìm giá trị của x khi y=3
Bài 2. Cho hàm số
y= -3x
a) Vẽ đồ thị hàm số
b) Tìm trên đồ thị hàm số điểm có hoành độ bằng 2
c) Tìm trên đồ thị hàm số điểm có tung độ bằng -6
Bài 1:
a: x=0 => y=-1
x=1 =>y=1
Đúng 1
Bình luận (0)
cho hàm số y=ax+b. Xác định hàm số
a) a=1 và đồ thị hàm số cắt trục tung tại điểm có tung dộ =3. vẽ đồ thị vừa tìm
b) b=3 đồ thị hàm số song song vs đg thẳng y=2x+1
c) dồ thị hàm số là đg thẳng di qua gốc tọa dộ và di qua diểm A(1;-3)
a: Thay x=0 và y=3 vào y=x+b, ta được:
b+0=3
hay b=3
Đúng 0
Bình luận (0)
Giúp mik với, mik cần gấp lắm!
Cho hàm số y=f(x)=-2x
a/ Vẽ đồ thị hàm số y=-2
b/ Điểm M(-2021; 4042) có thuộc đồ thị hàm số y=-2x không? Vì sao?
b: Vì \(y_M=4042=-2\cdot\left(-2021\right)=-2\cdot x_M\)
nên điểm M thuộc đồ thị
Đúng 0
Bình luận (0)
Bài 1 a) Khảo sát và vẽ đồ thị hàm số y=x³-2x²+x (C) b) từ đồ thị (C) suy ra đồ thị các hàm số sau: y=|x³-2x²+x|, y=|x|³ -2x²+|x| Bài 2: Khảo sát và vẽ đồ thị hàm số y=x⁴-2x²-3 (C). Từ đồ thị (C) suy ra đồ thị hàm số y=|y=x⁴-2x²-3|
Cho hàm số y=(m+2)x+m với m là tham số
a,,Tìm m để đồ thị hàm số cắt trục hoành tại điểm có hoành độ =2
b,,Tìm m để đồ thị hàm số cắt trục tung tại điểm có tung độ =2
Cho hàm sốa) Tìm a biết đồ thị hàm số đi qua điểm A(2;1).b) Với a vừa tìm được, tính giá trị của y(2),y(-1),y(2021) .c) Vẽ đồ thị hàm số với a vừa tìm được.
Cho hai đường thẳng (d):y=2x-2 và (d’) :y=(m+1) x+6 (m≠-1)
a)Vẽ đồ thị hàm số (d):y=2X-2
B)Tìm m để đồ thị hai hàm số (d)và (d’) có thị song song với nhau
c)Tìm m để khoảng cách từ gốc tọa độ o đến đường thẳng (d’) bằng 3√2
a: 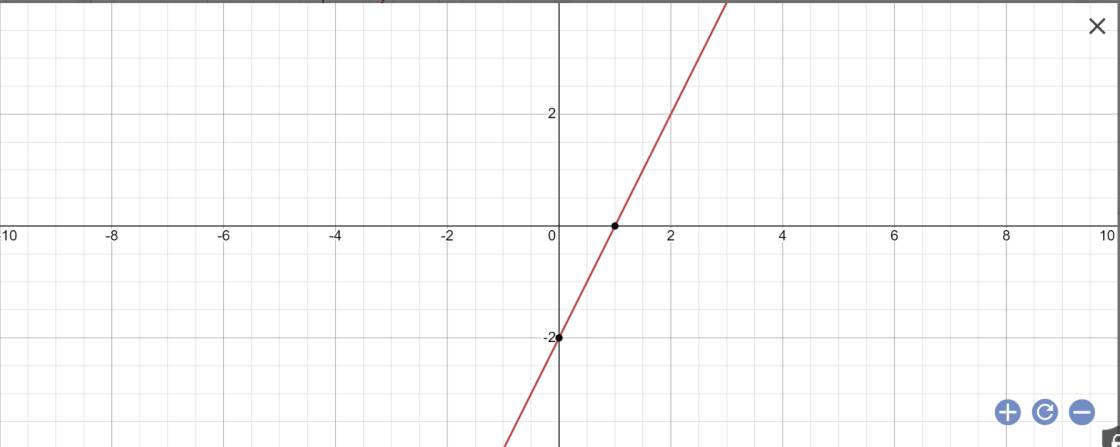
b: Để (d)//(d') thì \(\left\{{}\begin{matrix}m+1=2\\6< >-2\left(đúng\right)\end{matrix}\right.\)
=>m+1=2
=>m=1
c:
(d'): y=(m+1)x+6
=>(m+1)x-y+6=0
Khoảng cách từ O đến (d') là:
\(d\left(O;\left(d'\right)\right)=\dfrac{\left|0\cdot\left(m+1\right)+0\cdot\left(-1\right)+6\right|}{\sqrt{\left(m+1\right)^2+\left(-1\right)^2}}\)
\(=\dfrac{6}{\sqrt{\left(m+1\right)^2+1}}\)
Để \(d\left(O;\left(d'\right)\right)=3\sqrt{2}\) thì \(\dfrac{6}{\sqrt{\left(m+1\right)^2+1}}=3\sqrt{2}\)
=>\(\sqrt{\left(m+1\right)^2+1}=\sqrt{2}\)
=>\(\left(m+1\right)^2+1=2\)
=>\(\left(m+1\right)^2=1\)
=>\(\left[{}\begin{matrix}m+1=1\\m+1=-1\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}m=0\\m=-2\end{matrix}\right.\)
Đúng 2
Bình luận (0)















