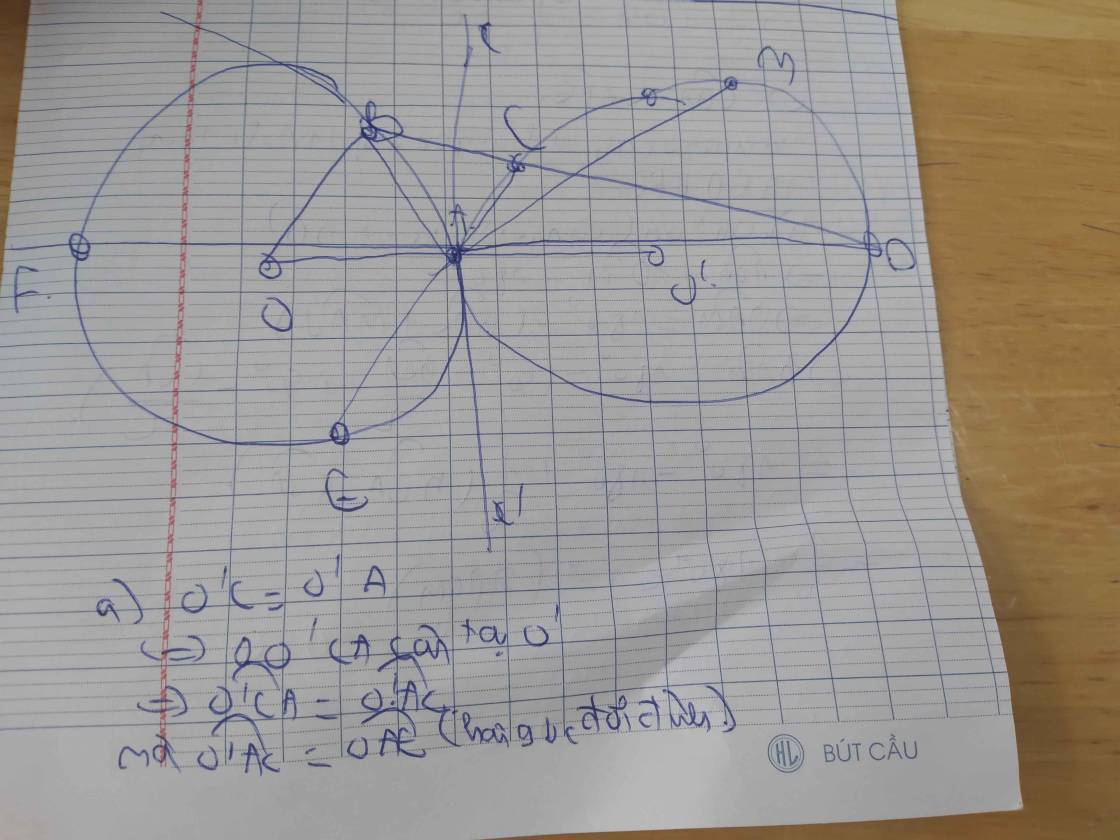
Cho (o) và (o’) tiếp xúc ngoài tại A.1 tiếp tuyến của (o) tại B cắt (o’) tại C và D(C nằm giữa B và D) .Các tia CA và DA cắt (o’) theo thứ tự tại E và F .a)CMR EF//CD b)Gọi M là điểm chính giữa của cung CD(M và A khác phía đối với CD ).Tính góc BAM

Những câu hỏi liên quan
Cho (o) và (o’) tiếp xúc ngoài tại A.1 tiếp tuyến của (o) tại B cắt (o’) tại C và D(C nằm giữa B và D) .Các tia CA và DA cắt (o’) theo thứ tự tại E và F .a)CMR EF//CD b)Gọi M là điểm chính giữa của cung CD(M và A khác phía đối với CD ).Tính góc BAM
cho 2 đường tròn (o) (o') tiếp xúc ngoài tại a. 1 tiếp tuyến của đường tròn (o) tại B cắt (o') tại c và d (c nằm giữa d và b ) . các tia ca,da cắt (o) tại e và f
a) kẻ tiếp tuyênd chung xAx' của 2 đường tròn chứng minh ef//cd
b) gọi m là điểm chính giữa của cung cd (m và a khác phía đối với cd) chứng minh rằng BAM = 90 độ
Cho hai đường tròn (o) và (o') tiếp xúc ngoài với nhau tại A . Một tiếp tuyến của đường tròn O tại điểm B cắt đường tròn (o') tại C và D các tia CA DAcắt đường tròn O theo thứ tự tại E và F
Chứng minh EF song song với CD
Gọi M là điểm chính giữa cung CD tính số đo góc BAM
Cho hai đường tròn (O) và (O’) tiếp xúc ngoài với nhau tại điểm A. Một tiếp tuyến của đường tròn (O) tại điểm B cắt (O’) tại C và D (C nằm giữa B và D). Các tia CA, DA cắt (O) tại E và F. a. Kẻ tiếp tuyến chung của hai đường tròn. Chứng minh rằng . b. Gọi M là điểm chính giữa của cung CD (M và A khác phía đối với CD). Chứng minh rằng .
Cho hai đường tròn (O) và (O’) tiếp xúc ngoài với nhau tại điểm A. Một tiếp tuyếncủa đường tròn (O) tại điểm B cắt (O’) tại C và D (C nằm giữa B và D). Các tia CA, DA cắt(O) tại E và F.a. Kẻ tiếp tuyến chung xAx của hai đường tròn. Chứng minh rằng EF//CD .b. Gọi M là điểm chính giữa của cung CD (M và A khác phía đối với CD). Chứngminh rằng BAM90 độ .
Đọc tiếp
Cho hai đường tròn (O) và (O’) tiếp xúc ngoài với nhau tại điểm A. Một tiếp tuyến
của đường tròn (O) tại điểm B cắt (O’) tại C và D (C nằm giữa B và D). Các tia CA, DA cắt
(O) tại E và F.
a. Kẻ tiếp tuyến chung xAx' của hai đường tròn. Chứng minh rằng EF//CD .
b. Gọi M là điểm chính giữa của cung CD (M và A khác phía đối với CD). Chứng
minh rằng BAM=90 độ .
Câu 1: Cho (O;R) và điểm A nằm ngoài đường tròn (O). Vẽ 2 tiếp tuyến AB, AC của (O) (B,C: tiếp điểm). Vẽ cát tuyến ADE của (O); D nằm giữa D & E; tia AD nằm giữa 2 tia AB và AO.a) Gọi H là giao điểm của OA và BC. C/m: DEOH nội tiếpb) Đường thẳng AO cắt (O) tại M và N (M nằm giữa A và O). C/m: EH.AD MH.ANCâu 2: Cho nửa đường tròn tâm (O;R) đường kính AB và điểm C trên đường tròn sao cho CACB. Gọi M là trung điểm của dây cung AC. Nối BM cắt cung AC tại E; AE và BC kéo dài cắt nhau tại D.a) C/m: MO...
Đọc tiếp
Câu 1: Cho (O;R) và điểm A nằm ngoài đường tròn (O). Vẽ 2 tiếp tuyến AB, AC của (O) (B,C: tiếp điểm). Vẽ cát tuyến ADE của (O); D nằm giữa D & E; tia AD nằm giữa 2 tia AB và AO.
a) Gọi H là giao điểm của OA và BC. C/m: DEOH nội tiếp
b) Đường thẳng AO cắt (O) tại M và N (M nằm giữa A và O). C/m: EH.AD= MH.AN
Câu 2: Cho nửa đường tròn tâm (O;R) đường kính AB và điểm C trên đường tròn sao cho CA=CB. Gọi M là trung điểm của dây cung AC. Nối BM cắt cung AC tại E; AE và BC kéo dài cắt nhau tại D.
a) C/m: MOCD là hình bình hành
b) Vẽ đường tròn tâm E bán kính EA cắt (O) tại điểm thứ 2 là N. Kẻ EF vuông góc với AC, EF cắt AN tại I, cắt (O) tại điểm thứ 2 là K; EB cắt AN tại H. C/m: BHIK nội tiếp.
Câu 3: Cho (O;R). Từ điểm S nằm ngoài đường tròn sao cho SO=2R. Vẽ tiếp tuyến SA,SB (A,B là tiếp tuyến). Vẽ cát tuyến SDE (D nằm giữa S và E), điểm O nằm trong góc ESB. Từ O kẻ đường vuông góc với OA cắt SB tại M. Gọi I là giao điểm của OS và (O).
a) C/m: MI là tiếp tuyến của (O)
b) Qua D kẻ đường vuông góc với OB cắt AB tại H và EB tại K. C/m: H là trung điểm của DK.
cho đường tròn tâm O và điểm A nằm ngoài đường tròn.một cát tuyến qua A cắt đường tròn (O) tại B và C( B nằm giữa A và C) các tiếp tuyến của (O) tại B và C cắt nhau tại D Đường thẳng D vuông góc với OA cắt (O) tại E và F( E nằm giưa D và F ) gọi M là giao điểm của DO và và BC
1.Cho (O;R). Qua điểm M nằm trong đương tròn vẽ các dây CD và EF không đi qua O. Tiếp tuyến tại C và D của (O) cắt nhau ở A, tiếp tuyến tại E và F của (O) cắt nhau tại B. Chứng minh OM vuông góc với AB2. Cho (O) và đường thẳng d không cắt (O). Gọi H là hình chiếu của (O) trên d. Từ H vẽ các cát tuyến HCD và HAB với (O) (C nằm giữa H và D, A nằm giữa H và B, các cát tuyến không đi qua O). Tiếp tuyến tại A của (O) cắt d tại M. Tiếp tuyến tại C của (O) cắt d tại M. Chứng minh ΔOMN cân
Đọc tiếp
1.Cho (O;R). Qua điểm M nằm trong đương tròn vẽ các dây CD và EF không đi qua O. Tiếp tuyến tại C và D của (O) cắt nhau ở A, tiếp tuyến tại E và F của (O) cắt nhau tại B. Chứng minh OM vuông góc với AB
2. Cho (O) và đường thẳng d không cắt (O). Gọi H là hình chiếu của (O) trên d. Từ H vẽ các cát tuyến HCD và HAB với (O) (C nằm giữa H và D, A nằm giữa H và B, các cát tuyến không đi qua O). Tiếp tuyến tại A của (O) cắt d tại M. Tiếp tuyến tại C của (O) cắt d tại M. Chứng minh ΔOMN cân
1.Cho (O;R). Qua điểm M nằm trong đương tròn vẽ các dây CD và EF không đi qua O. Tiếp tuyến tại C và D của (O) cắt nhau ở A, tiếp tuyến tại E và F của (O) cắt nhau tại B. Chứng minh OM vuông góc với AB2. Cho (O) và đường thẳng d không cắt (O). Gọi H là hình chiếu của (O) trên d. Từ H vẽ các cát tuyến HCD và HAB với (O) (C nằm giữa H và D, A nằm giữa H và B, các cát tuyến không đi qua O). Tiếp tuyến tại A của (O) cắt d tại M. Tiếp tuyến tại C của (O) cắt d tại M. Chứng minh ΔOMN cân
Đọc tiếp
1.Cho (O;R). Qua điểm M nằm trong đương tròn vẽ các dây CD và EF không đi qua O. Tiếp tuyến tại C và D của (O) cắt nhau ở A, tiếp tuyến tại E và F của (O) cắt nhau tại B. Chứng minh OM vuông góc với AB
2. Cho (O) và đường thẳng d không cắt (O). Gọi H là hình chiếu của (O) trên d. Từ H vẽ các cát tuyến HCD và HAB với (O) (C nằm giữa H và D, A nằm giữa H và B, các cát tuyến không đi qua O). Tiếp tuyến tại A của (O) cắt d tại M. Tiếp tuyến tại C của (O) cắt d tại M. Chứng minh \(ΔOMN\) cân
1.Cho (O;R). Qua điểm M nằm trong đương tròn vẽ các dây CD và EF không đi qua O. Tiếp tuyến tại C và D của (O) cắt nhau ở A, tiếp tuyến tại E và F của (O) cắt nhau tại B. Chứng minh OM vuông góc với AB
2. Cho (O) và đường thẳng d không cắt (O). Gọi H là hình chiếu của (O) trên d. Từ H vẽ các cát tuyến HCD và HAB với (O) (C nằm giữa H và D, A nằm giữa H và B, các cát tuyến không đi qua O). Tiếp tuyến tại A của (O) cắt d tại M. Tiếp tuyến tại C của (O) cắt d tại M. Chứng minh ΔOMN cân
Đúng 0
Bình luận (0)