tim x y ϵ N
(X+1)+(2y-1)
Tim x , y ϵ N thỏa mãn :
\(2017^x+1+\left|y-2016\right|=y-2016\)
Tim x , y ϵ N thỏa mãn :
\(2017^x+1+\left|y-2016\right|=y-2016\)
làm lại
Ta có : xϵN nên 2017^x>0. Mà|y−2016|>0
=>2017^x+1+|y−2016|>0=>y−2016>0
=>|y−2016|=y−2016
Ta lại có
2017^x+1+y−2016=y−2016
=>2017^x+1=0
=>2017^x=-1(vô lý vì 2017^x>0)
Từ trên suy ra không có giá trị x, y thỏa mãn đề bài
Vậy không có giá trị x, y thỏa mãn đề bài
Vì x là số tự nhiên nên 2017^x>0.
Mà ![]() y-2016
y-2016 ![]() >0
>0
Suy ra: 2017^x+1+![]() y-2016
y-2016 ![]() >0
>0
=>y-2016>0=>![]() y-2016
y-2016 ![]() =y-2016
=y-2016
Ta có
2017^x+1+y-2016=y-2016
=>2017^x+1=0
=>2017^x=-1(vô lý vì 2017^x>0)
Từ trên suy ra : không có giá trị cuả x,y thỏa mãn đề bài
Vậy không có giá trị cuả x,y thỏa mãn đề bài
Tìm x, y ϵ Z biết :
(x + 1)(2y – 5) = 143
Ta thấy (x+1)(2y-5)=143=11.13=13.11=143.1=1.143
Suy ra ta có 4 trường hợp sau:
-Nếu x+1=11suy ra x=10 ; 2y-5=13 suy ra y=9
-Nếu x+1=13 suy ra x=12 ; 2y-5=11 suy ra y=8
-Nếu x+1=143 suy ra x=142 ; 2y-5=1 suy ra y=3
-Nếu x+1=1 suy ra x=0 ; 2y-5=143 suy ra y=74
Vậy x=10 thì y=9
x=12 thì y=8
x=142 thì y=3
x=0 thì y=74
bài 4 tìm x;y ϵ N
a 2y*(3x-1)+9x-3=7
b 3xy-2x+3y-9=0
Lời giải:
a. $2y(3x-1)+9x-3=7$
$2y(3x-1)+3(3x-1)=7$
$(3x-1)(2y+3)=7$
Vì $3x-1, 2y+3$ đều là số nguyên với mọi $x,y\in N$, và $2y+3>0$ nên ta có bảng sau: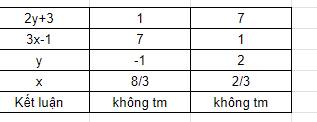
b.
$3xy-2x+3y-9=0$
$x(3y-2)+3y-9=0$
$x(3y-2)+(3y-2)-7=0$
$(3y-2)(x+1)=7$
Đến đây bạn cũng lập bảng tương tự như phần a.
Tìm x,y ϵ Z:
3x-2y+6xy=1
Lời giải:
$3x-2y+6xy=1$
$\Rightarrow (3x+6xy)-(2y+1)=0$
$\Rightarrow 3x(1+2y)-(2y+1)=0$
$\Rightarrow (1+2y)(3x-1)=0$
$\Rightarrow 1+2y=0$ hoặc $3x-1=0$
$\Rightarrow y=\frac{-1}{2}$ hoặc $x=\frac{-1}{3}$ (vô lý vì $x,y$ là số nguyên)
Vậy không tồn tại $x,y$ thỏa mãn đề.
Tìm x; y (x < y) biết x ϵ N*, y ϵ N* và \(\dfrac{1}{x}\) + \(\dfrac{1}{y}\) = \(\dfrac{1}{8}\)
Lời giải:
$\frac{1}{x}+\frac{1}{y}=\frac{1}{8}$
$\Rightarrow \frac{x+y}{xy}=\frac{1}{8}$
$\Rightarrow 8(x+y)=xy$
$\Rightarrow xy-8x-8y=0$
$\Rightarrow x(y-8)-8(y-8)=64$
$\Rightarrow (x-8)(y-8)=64$
Do $x,y$ tự nhiên nên $x-8,y-8\in\mathbb{Z}$
$\Rightarrow x-8$ là ước của $64$. Mà $x-8>-8$ với mọi $x\in\mathbb{N}^*$ nên:
$x-8\in\left\{1; 2; 4; 8; 16; 32; 64; -1; -2; -4\right\}$
Đến đây bạn chỉ cần chịu khó xét các TH là được.
Bài 4: tìm x,y ϵ Z, biết:
a) (x - 3) (2y - 6) = 5
b) (2x + 1) (y + 2)= 10
c) xy - 5x + 2y = 7
d) xy - 3x - 4y = 5
a, \(x,y\in Z\Rightarrow\left\{{}\begin{matrix}x-3,2y-6\in Z\\x-3,2y-6\inƯ\left(5\right)=\left\{\pm1;\pm5\right\}\end{matrix}\right.\)
Ta có bảng:
| x-3 | -1 | -5 | 1 | 5 |
| 2y-6 | -5 | -1 | 5 | 1 |
| x | 2 | -2 | 4 | 8 |
| y | \(\dfrac{1}{2}\left(loại\right)\) | \(\dfrac{5}{2}\left(loại\right)\) | \(\dfrac{11}{2}\left(loại\right)\) | \(\dfrac{7}{2}\left(loại\right)\) |
Vậy không có x,y thỏa mãn đề bài
b, tương tự câu a
\(c,xy-5x+2y=7\\ \Rightarrow x\left(y-5\right)+2y-10=-3\\ \Rightarrow x\left(y-5\right)+2\left(y-5\right)=-3\\ \Rightarrow\left(x+2\right)\left(y-5\right)=-3\)
Rồi làm tương tự câu a
\(d,xy-3x-4y=5\\ \Rightarrow x\left(y-3\right)-4y+12=17\\ \Rightarrow x\left(y-3\right)-4\left(y-3\right)=17\\ \Rightarrow\left(x-4\right)\left(y-3\right)=17\)
Rồi làm tương tự câu a
Bài 1: Tìm số tự nhiên nhỏ nhất có:
a) 7 ước
b) 15 ước
Bài 2: Tìm x,y ϵ N biết:
a) (2x+1) . (y-3)=10
b) (3x -2) . (2y -3)=1
c) (x+1) . (2y-1)=12
d) x+6 = y(x-1)
e) x-3 = y(x+2)
a)(2x+1).(y-3)=10
có:10=1.10=2.5=10.1=5.2
xét:2x+1=1 ; y-3=10
2x=1-1=0 y=10+3=13(nhận)
x=0:2=0(nhận)
......(xét tiếp các trường hợp còn lại)
Vậy............
b)(3x-2).(2y-3)=1
\(\Leftrightarrow\) 3x-2=1 hoặc 2y-3=1
3x=1+2=3 2y=1+3=4
x=3:3=1 y=4:2=2
Vậy x=1 và y=2
c làm tương tự phần a