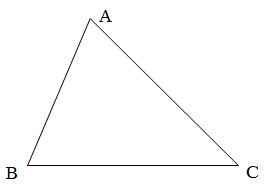
Cho tam giác ABC có ba góc nhọn ( AB<AC). Vẽ về phía ngoài tam giác ABC các tam giác đều ABD, ACE. Gọi I là giao điểm của CD và BE, K là giao điểm của AB và DC.
a) Chứng minh rằng: Δ ADC= ΔABe
b) Chứng minh rằng: ∠ DIB = 60o
c) Gọi M và N là trung điểm của CD và BE. Chứng minh rằng \(\Delta AMN\) đều
d) Chứng minh rằng: IA là tia phân giác của góc DIE