Cho ΔABC có AB=12cm, AC=5cm, BC=13cm
a. ΔABC là tam giác gì? Vì sao?
b. Gọi I là giao điểm của các tia phân giác của góc B và góc C , qua O kẻ DE//BC (D ∈ AB, E ∈ AC). Chứng minh ΔIDB và ΔICE cân. Chứng minh rằng DE = BD + ẺC
Bài 4 Cho ΔABC có AB = 5cm, AC = 12cm, BC = 13cm. a) Chứng minh ΔABC vuông. b) Vẽ tia phân giác của góc B cắt cạnh AC tại E. Từ E kẻ ED vuông góc BC. Chứng minh BA = BD, EA = ED. c) Gọi K là giao điểm của hai tia BA và DE. Chứng minh EK = EC.
Tin nhắn đã được thu hồi
a: Xét ΔABC có \(BC^2=AB^2+AC^2\)
nên ΔABC vuông tại A
b: Xét ΔBAE vuông tại A và ΔBDE vuông tại D có
BE chung
\(\widehat{ABE}=\widehat{DBE}\)
Do đó: ΔBAE=ΔBDE
Suy ra: BA=BD; EA=ED
c: Xét ΔAEK vuông tại A và ΔDEC vuông tại D có
EA=ED
\(\widehat{AEK}=\widehat{DEC}\)
Do đó:ΔAEK=ΔDEC
Suy ra: EK=EC
Phần1: Cho tam giác ABC vuông tại A, có B = 60 và AB = 5cm. Tia phân giác của góc B cắt AC tại D. Kẻ vuông góc với BC tại E. Chứng minh:
a:KC vuông góc với AC
b:AK song song với BC
Phần2: Cho tam giác ABC có AB = 12cm, AC = 5cm, BC = 13cm. Chứng minh:
a:ABC là tam giác gì? Vì sao?
b:Gọi I là giao điem của các tia phân giác của góc B và C, qua I kẻ DE song song BC ( D thuộc AB, E thuộc AC)
Chứng minh: tam giác IDB cân và DE = BD + EC
Ai giải 2 phần này giúp mình nha!
Cho ΔABC vuông tại B có góc C bằng 30 độ. Tia phân giác của góc A cắt BC tại M. Kẻ MN vuông góc với AC (N ∈ AC).
a) Chứng minh rằng AB = AN
b) Gọi I là giao điểm của NM và AB. Chứng minh ΔIMB = ΔCMN
c) ΔIAC là tam giác gì? Vì sao?
d) Tính BC biết AC = 8cm
a,Ta có : ABC^+BAC^+BCA^=180* ( đl tổng 3 góc )
=> 90*+BAC^+30*=180*
=>BAC^=180*-120*=60*
Do AM là tia p/g của BAC^
=> BAM^=MAN^=60*/2=30*
Xét tam giác vuông ABM và tam giác vuông ANM
AM cạnh chung
BAM^=MAN^
=>tam giác ABM = tam giác ANM ( ch-gn )
=>AB=AN (2 cạnh tương ứng)
b,Xét tam giác vuông IBM và tam giác vuông CNM
BMI^=NMC^ ( đối đỉnh )
BM = NM ( cm câu a )
=> tam giác IBM = tam giác CNM ( cgv-gn )
c, Ta có : BMI^ + MBI^ + BIM ^ = 180*
=>BMI^ + 90* + 30* = 180*
=> BMI^=180*-120*=60*
Do BMI^=CMN^
=>BMI^=CMN^=60*
Lại có IMN^=180* ( góc bẹt )
Mà : IMC^+CMN^=180*
=>IMC^=180*-60*=120*
Mặt khác : IM=MC (cm câu b)
=> tam giác IMC cân tại M
=>MIC^=MCI^
dễ thấy : IMC^+MIC^+MCI^=180*
=>MIC^+MCi^=180*-120*=60*
do :MIC^=MCI^
=>MIC^=MCI^=60*/2=30*
Ta có :+)AIC^=BIM^+CIM^=30*+30*=60*
+)ACI^=NCM^+MCI^=30*+30*=60*
+)IAC^=60*
=>tam giác IAC là tam giác đều
cho tam giác ABC vuông có AB=3cm AC=4cm BC=5cm
a) tam giác ABC là tam giác gì vì sao
b) gọi H là hình chiếu của A trên BC tia phân giác góc BAH cắt BC tại D qua A kẻ đường thẳng song song với BC trên đó lấy E sao cho AE=BD (E và C cùng phía với AB) chứng minh AB=DE
c) chứng minh tam giác ADC cân
đ) gọi NH là trung điểm của AD,I là giao điểm của AH và ĐỂ chứng minh C,I,M thẳng hàng
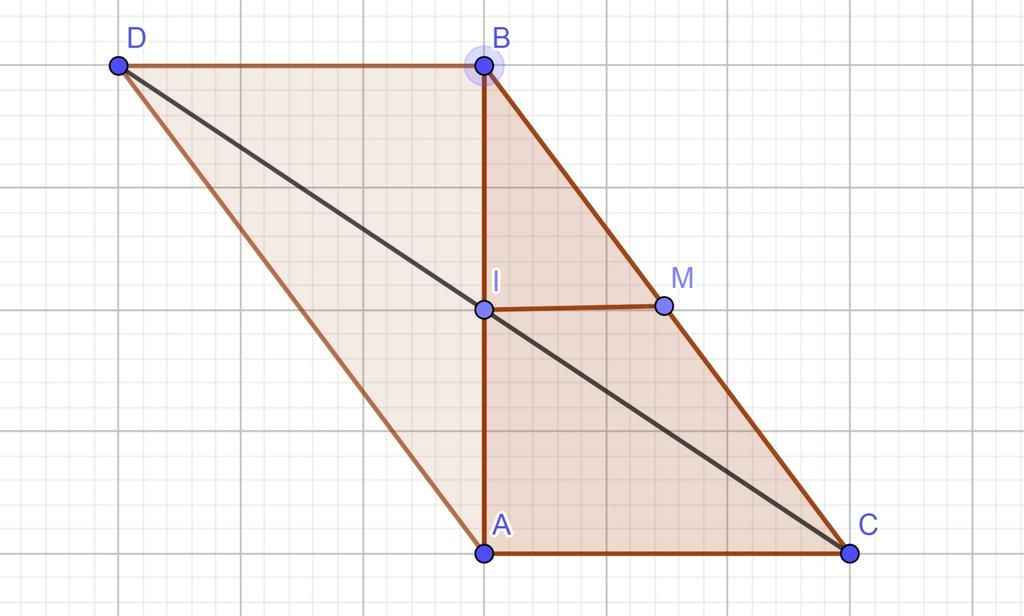
Cho tam giác ABC có A= 90 độ, AC = 5cm, BC = 13cm. Gọi I là trung điểm của cạnh AB, D là điểm đối xứng với C qua I.
a) Tứ giác ADBC là hình gì? Vì sao?
b) Gọi M là trung điểm của cạnh BC. Chứng minh: MI vuông góc với AB. Tính diện tích ΔABC.
a) Xét tứ giác \(ADBC\) ta có :
\(IB=IA\left(g.t\right)\)
\(IC=IC\) ( \(D\) đối xứng qua \(I\))
Vì tứ giác có 2 đường chéo cắt nhau tại trung điểm mỗi đường
Vậy tứ giác \(ADBC\) là hình bình hành
b) Xét \(\Delta ABC\) ta có :
\(IA=IB\left(g.t\right)\)
\(MB=MC\left(g.t\right)\)
\(\Rightarrow IM\) là đường trung bình \(\Delta ABC\)
Do đó : \(IM\text{/ / }AC\)
Mà \(AB\text{⊥}AC\left(A=90^o\right)\)
Vậy \(IM\text{⊥}AB\)
Áp dụng định lí pytago \(\Delta ABC\) ta có :
\(BC^2=AB^2+AC^2\)
\(\Rightarrow AB=\sqrt{BC^2-AC^2}=\sqrt{13^2-5^2}=12\left(cm\right)\)
\(S_{\Delta ABC}=\dfrac{1}{2}.AB.AC=\dfrac{1}{2}.13.5=30\left(cm^2\right)\)
Cho ΔABC có 3 góc nhọn, AB < AC < BC. Các tia phân giác của góc A và góc C cắt nhau tại O. Từ O kẻ OF ⊥ BC, từ O kẻ OH ⊥ AC. Lấy điểm I trên đoạn FC sao cho FI = AH. Gọi K là giao điểm của FH và AI a. Chứng minh ΔFCH cân b. Chứng minh OK = OI c. Goi M la diem tren doan HF sao cho MI=IF .Chung minh MI song song viu AC.D,Chunng minh k la trung diem cua DE.e,chứng minh BD la phan giac ABC.,f,chứng minh B,O,K thẳng hàng
Cho ΔABC có 3 góc nhọn, AB < AC < BC. Các tia phân giác của góc A và góc C cắt nhau tại O. Từ O kẻ OF ⊥ BC, từ O kẻ OH ⊥ AC. Lấy điểm I trên đoạn FC sao cho FI = AH. Gọi K là giao điểm của FH và AI a. Chứng minh ΔFCH cân b. Chứng minh OK = OI c. Goi M la diem tren doan HF sao cho MI=IF .Chung minh MI song song viu AC.D,Chunng minh k la trung diem cua DE.e,chung minh BD la phan giac ABC.,f,chung minh B,O,K thang hang
Bài 3: Cho ΔABC vuông tại A , vẽ tia phân giác BD của góc ABC (D AC). Trên cạnh BC lấy điểm E sao cho BE = AB . a) Chứng minh: ΔABD = ΔEBD b) Chứng minh: Tam giác ADE là tam giác cân. Vẽ AH vuông góc với BC (H BC) . Chứng minh : AH // DE và BAH ACH c) Chứng minh: AE là tia phân giác của góc HAC. d) Gọi K là giao điểm của AB và ED. Chứng minh: AK = EC và AE //
a) Xét tgiac ABD và EBD có:
+ AB = BE
+ BD chung
+ góc ABD = EBD
=> Tgiac ABD = EBD (c-g-c)
=> đpcm
b) Tgiac ABD = EBD (cmt) => AD = DE (hai cạnh t/ứng)
Xét tgiac ADE có AD = DE => Tgiac ADE cân tại D
=> đpcm
c) AH \(\perp\)BC, DE\(\perp\)BC => AH\(//\)DE
=> góc HAE = AED (2 góc SLT do AH\(//\)DE)
Mà tgiac ADE cân tại D (cmt) => góc AED = DAE
=> góc HAE = DAE
=> AE là tia pgiac góc HAC (đpcm)
d) Xét tgiac ADK và EDC có:
+ góc DAK = DEC = 90o
+ góc ADK = EDC (2 góc đối đỉnh)
+ AD = DE (do tgiac ABD = EBD)
=> Tgiac ADK = EDC (g-c-g)
=> AK = EC và KD = DC (2 cạnh t/ứng)
=> Tgiac KDC cân tại K => Góc DCK = (180o- góc KDC) /2
Tgiac AED cân tại D => góc EAD = (180o- góc ADE) /2
Mà góc ADE = KDC (2 góc đối đỉnh) => góc DCK = EAD
Mà 2 góc này SLT => AE \(//\)KC
=> đpcm
Cho ΔABC vuông tại B có góc C bằng 30 độ. Tia phân giác của góc A cắt BC tại M. Kẻ MN vuông góc với Ac (N ∈ AC).
a) C/m rằng AB=AN.
b) Gọi I là giao điểm của NM và Ab. C/m ΔIMB = ΔCMN.
c) ΔIAC là tam giác gì? Vì sao?
d) Tính BC biết AC=8cm
mọi người ơi làm ơn giúp mình với ạaaaaaa
a: Xét ΔABM vuông tại B và ΔANM vuông tại N có
AM chung
\(\widehat{BAM}=\widehat{NAM}\)
Do đó:ΔABM=ΔANM
Suy ra: AB=AN
b: Xét ΔIMB vuông tại B và ΔCMN vuông tại N có
MB=MN
\(\widehat{IMB}=\widehat{CMN}\)
Do đó: ΔIMB=ΔCMN
c: Ta có: ΔIMB=ΔCMN
nên BI=NC
Ta có: AB+BI=AI
AN+NC=AC
mà AB=AN
và BI=NC
nên AI=AC
hay ΔAIC cân tại A
B1. Cho ΔABC có Aˆ=90∘. AB = AC, điểm D thuộc cạnh AB, điểm E thuộc cạnh AC sao cho AD = AE. Đường thẳng qua D và vuông góc với BE cắt đường thẳng CA ở K. CMR: AK = AC
B2. Cho ΔABC, I là trung điểm của AB, đường thẳng qua I và song song với BC cắt AC ở K. Đường thẳng qua K và song song với AB cắt BC ở H. CMR
a) KH = IB
b) AK = KC
B3. Cho ΔABC có Aˆ = 60∘. Tia phân giác của Bˆ cắt AC ở D, tia phân giác của Cˆ cắt AB ở E. Gọi O là giao điểm của BD và CE.
a) Tính BOCˆ
b) C/m CD = OE
B4. Cho ΔABC. Ở phía ngoài ΔABC vẽ các tam giác vuông tại A là ABD và ACE có AB = AD, AC = AE. Kẻ AH vuông góc với BC, gọi I là giao điểm của HA và DE. CMR: DI = IE
Giúp em với !! T7 phải nộp rồiii