Cho x, y, z \(\ge\)0 thỏa mãn x2017 + x2017 + x2017 = 3. Tìm GTLN : x2 + y2 + z2

Những câu hỏi liên quan
Cho x1−12017=x2−22016=x3−32016=...=x2017−20171x1−12017=x2−22016=x3−32016=...=x2017−20171 và x1+x2+...+x2017=2017.2018
Tìm x1,x2,...,x2017?
Cho x1−12017=x2−22016=x3−32016=...=x2017−20171x1−12017=x2−22016=x3−32016=...=x2017−20171 và x1+x2+...+x2017=2017.2018
Tìm x1,x2,...,x2017?
Tính giá trị biểu thức:a) A 3
x
2
- 2
(
x
-
y
)
2
- 3
y
2
tại x 4 và y -4;b) B 4(x - 2)(x +1) +
(
2
x
-
...
Đọc tiếp
Tính giá trị biểu thức:
a) A = 3 x 2 - 2 ( x - y ) 2 - 3 y 2 tại x = 4 và y = -4;
b) B = 4(x - 2)(x +1) + ( 2 x - 4 ) 2 + ( x + 1 ) 2 tại x = - 1 2 ;
c*) C = x 2 (y-z) + y 2 (z-x) + z 2 (x-y) tại x = 6, y = 5 và z = 4;
d*) D = x 2017 - 10 x 2016 + 10 x 2015 - . . . - 10 x 2 + l0x -10 với x = 9.
a) Tìm được A = (x- y)(x + 5y).
Thay x = 4 và y = -4 vào A tìm được A = -128.
b) Tìm được B = 9 ( x - 1 ) 2 .
Thay x = - 4 vào B tìm được B = 81 4 .
c) Tìm được C = (x - y)(y - z)(x - z).
Thay x = 6,y = 5 và z = 4 vào C tìm được C = 2.
d) Thay 10 = x +1 vào D và biến đổi ta được D = -1.
Đúng 1
Bình luận (0)
Cho \(\dfrac{x1-1}{2017}=\dfrac{x2-2}{2016}=\dfrac{x3-3}{2016}=...=\dfrac{x2017-2017}{1}\) và x1+x2+...+x2017=2017.2018
Tìm x1,x2,...,x2017?
cái chỗ x3-3/2016 phải là x3-3/2015, viết lộn
Đúng 0
Bình luận (0)
cho x, y, z ≥ 0 thỏa mãn x + y + z =6. Tìm GTNN và GTLN của
A = x2 + y2 + z2
Bạn tham khảo lời giải tại đây:
cho \(x,y,z\ge0\) thỏa mãn \(x y z=6\). tìm GTLN và GTNN của biểu thức \(A=x^2 y^2 z^2\) - Hoc24
Đúng 0
Bình luận (0)
a)x2016=x2017
b)(x-5)2015=(x-5)2014
c5x+5x+2=650
d)x2017=x2
a) x=1 hoặc x=0
b) x=5 hoặc x=6
c) x=64,8
d) x=1 hoặc x=0
Đúng 0
Bình luận (0)
a) 2016x = 2017x
=> 2016x - 2017x =0
=> x(2016 - 2017) =0
=> x(-1)=0
=>x=0:(-1)=0
b) (x-5)2015=(x-5)2014
=> (x-5)2015 - (x-5)2014=0
=> (x-5)(2015-2014)=0
=> x-5=0
=>x=5
c)5x + 5x +2 =650
=> 10x + 2 =650
=> 10x =648
=> x = \(\frac{648}{10}=64,8\)
d) 2017x =2x
=> 2017x -2x =0
=> 2015x=0
=>x=0
Đúng 0
Bình luận (0)
Cho hàm số f(x) có đạo hàm trên R thỏa mãn
f
(
x
)
-
2018
f
(
x
)
2018
.
2017
.
x
2017
.
e
2018
x
với mọi
x
∈
R
;
f
(
0
)
2018
.
Giá trị của f(1) là A. ...
Đọc tiếp
Cho hàm số f(x) có đạo hàm trên R thỏa mãn f ' ( x ) - 2018 f ( x ) = 2018 . 2017 . x 2017 . e 2018 x với mọi x ∈ R ; f ( 0 ) = 2018 . Giá trị của f(1) là
A. f ( 1 ) = 2018 e - 2018
B. f ( 1 ) = 2019 e - 2018
C. f ( 1 ) = 2018 e 2018
D. f ( 1 ) = 2019 e 2018
Cho hàm số f(x) có đạo hàm trên
ℝ
thỏa mãn f’(x) – 2018f(x) 2018.x2017.e2018x với mọi
x
∈
ℝ
và f(0) 2018. Tính giá trị f(1). A. f(1) 2019e2018. B. f(1) 2018e-2018. C. f(1) 2018e2018. D. f(1) 2017e2018.
Đọc tiếp
Cho hàm số f(x) có đạo hàm trên ℝ thỏa mãn f’(x) – 2018f(x) = 2018.x2017.e2018x với mọi x ∈ ℝ và f(0) = 2018. Tính giá trị f(1).
A. f(1) = 2019e2018.
B. f(1) = 2018e-2018.
C. f(1) = 2018e2018.
D. f(1) = 2017e2018.
Chọn A

Lấy tích phân từ 0 đến 1 của 2 vế:
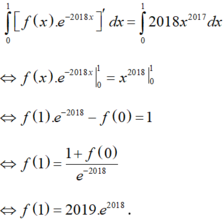
Đúng 0
Bình luận (0)
Các số thực a,b,c,x,y,z thỏa mãn
a
2
+
b
2
+
c
2
-
2
a
+
4
c
+
4
0
và
x
2
+
y
2
+
z
2
-
4
x
+
4
y
+
4...
Đọc tiếp
Các số thực a,b,c,x,y,z thỏa mãn a 2 + b 2 + c 2 - 2 a + 4 c + 4 = 0 và x 2 + y 2 + z 2 - 4 x + 4 y + 4 = 0 . Tìm GTLN của S = a - x 2 + b - y 2 + z - c 2 .
![]()
![]()
![]()
![]()
Cmr nếu x/y=z/t thì [(x-y)/(z-t)]2017=(x2017+y2017)/(z2017+t2017)













