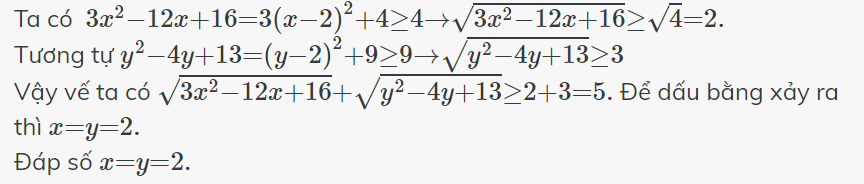giai p.t : \(\sqrt{3x^2-12x+16}+\sqrt{y^2-4y+13}=5\)
Những câu hỏi liên quan
Giải pt:
\(\sqrt{3x^2-12x+16}+\sqrt{y^2-4y+13}=5\)
28 tháng 5 2022 lúc 22:20
Giải phương trình:
\(\sqrt{4x^2-12x+16}+\sqrt{y^2-4y+13}=5\)
24 tháng 2 2022 lúc 22:38
giải phương trình: \(\sqrt{3x^2-12x-6}\) +\(\sqrt{y^2-4y+13}\) =5
a)\(\sqrt{3x^2-12x+16}+\sqrt{y^2-4y+13}=5\)
b)\(x^2+4x+5=2\sqrt{2x+3}\)
b/ \(\Rightarrow2x+3+2\sqrt{2x+3}-x^2-6x-8=0\)
Đặt \(a=\sqrt{2x+3}\left(a\ge0\right)\)
\(\left(1\right)\Rightarrow a^2+2a-x^2-6x-8=0\)
Có: \(\Delta=1+x^2+6x+8=x^2+6x+9=\left(x+3\right)^2\)
\(\Rightarrow\sqrt{\Delta}=x+3\)
\(\Rightarrow a=\frac{-1+x+3}{1}=x+2\)
hoặc \(a=\frac{-1-x-3}{1}=-x-4\)
+) Với a = x + 2 \(\Leftrightarrow\sqrt{2x+3}=x+2\left(x\ge-2\right)\)
......... tự giải ra x
+) Với a = -x - 4 \(\Leftrightarrow\sqrt{2x+3}=-x-4\left(x\le-4\right)\)
.........tự giải ra x
Đúng 0
Bình luận (0)
a)\(\sqrt{x-5}-\frac{x-14}{3+\sqrt{x-5}}=3\)
b)\(\sqrt{3x^2-12x+16}+\sqrt{y^2-4y+13}=5\)
c) \(3x^2+2x=2\sqrt{x^2+x}+1-x\)
a) Đk: x \(\ge\) 5
\(\sqrt{x-5}-\frac{x-14}{3x+\sqrt{x-5}}=3\)
\(\sqrt{x-5}\left(3+\sqrt{x-5}\right)-\frac{x-14}{3\sqrt{x-3}}\left(3+\sqrt{x-5}\right)=3\left(3+\sqrt{x-5}\right)\)
\(\sqrt{x-5}\left(3+\sqrt{x-5}\right)-\left(x-14\right)=3\left(3+\sqrt{x-5}\right)\)
\(3\sqrt{x-5}+9-\left(3\sqrt{x-5}+9\right)=9+3\sqrt{x-5}-\left(3\sqrt{x-5}+9\right)\)
=> Luôn đúng với x \(\ge\) 5
chúc bạn học tốt
Đúng 0
Bình luận (0)
giúp mk vs mk cảm ơn nhiều lắm
GIải phương trình: \(\sqrt{3x^2-12x+16}\) +\(\sqrt{y^2-4y+13}\)=5
Bạn tham khảo lời giải của tớ nha!
Nhờ các thầy cô trên Online Math giải giùm e câu này:
x+y+z = 3
Tìm Max P = \(\sqrt{3x^2-12x+16}-\sqrt{y^2-4y+13}=5\)
Giai PT:
a,\(x^2-7x+\sqrt{x^2-7x+8}=12\)
b,\(\sqrt{3x^2+12x+16}+\sqrt{y^2+4x^2+13}=5\)
c.\(\sqrt{x-3}+\sqrt{5-x}=x^2-8x+18\)
Giải phương tình:
a) \(x^2-7x+\sqrt{x^2-7x+8}=12
\)
b)\(\sqrt{3x^2+12x+16}+\sqrt{y^2-4y+13}=5\)
c)\(\sqrt{x-3}+\sqrt{5-x}=x^2-8x+18\)
a) ĐK: x2 - 7x + 8 ≥ 0
Đặt √(x2 - 7x + 8) = a (1)
⇔ a2 + a - 20 = 0
⇔ a = 4 hoặc a = -5
Thay vào (1) là tìm được x, kết hợp với ĐK là xong.
Đúng 0
Bình luận (0)
b) Dễ chứng minh Vế Trái lớn hơn hoặc bằng 0.
Dấu "=" xảy ra khi x = -4; y= 4. ....... là nghiệm của pt
Đúng 0
Bình luận (2)