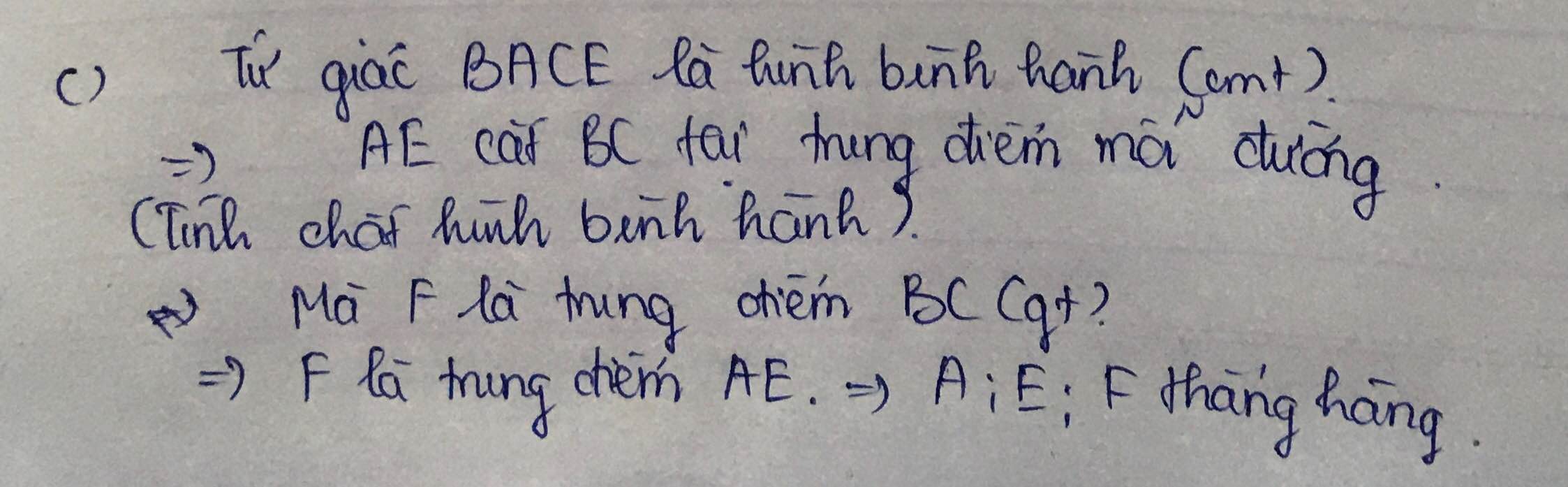Chứng minh \(E=mc^2\)

Những câu hỏi liên quan
Cho tam giác ABC. Lấy M là một điểm nằm trong tam giác
a) Chứng minh tổng 3 đoạn thẳng (MA+MB+MC) lớn hơn một nửa chu vi tam giác ABC
b)Lấy E là trung điểm đoạn MC. Vẽ EF vuông góc MC tại E. (F thuộc AC)
Chứng minh FM=FC
c)Chứng minh AC > AM
Vẽ luôn hình giúp mình
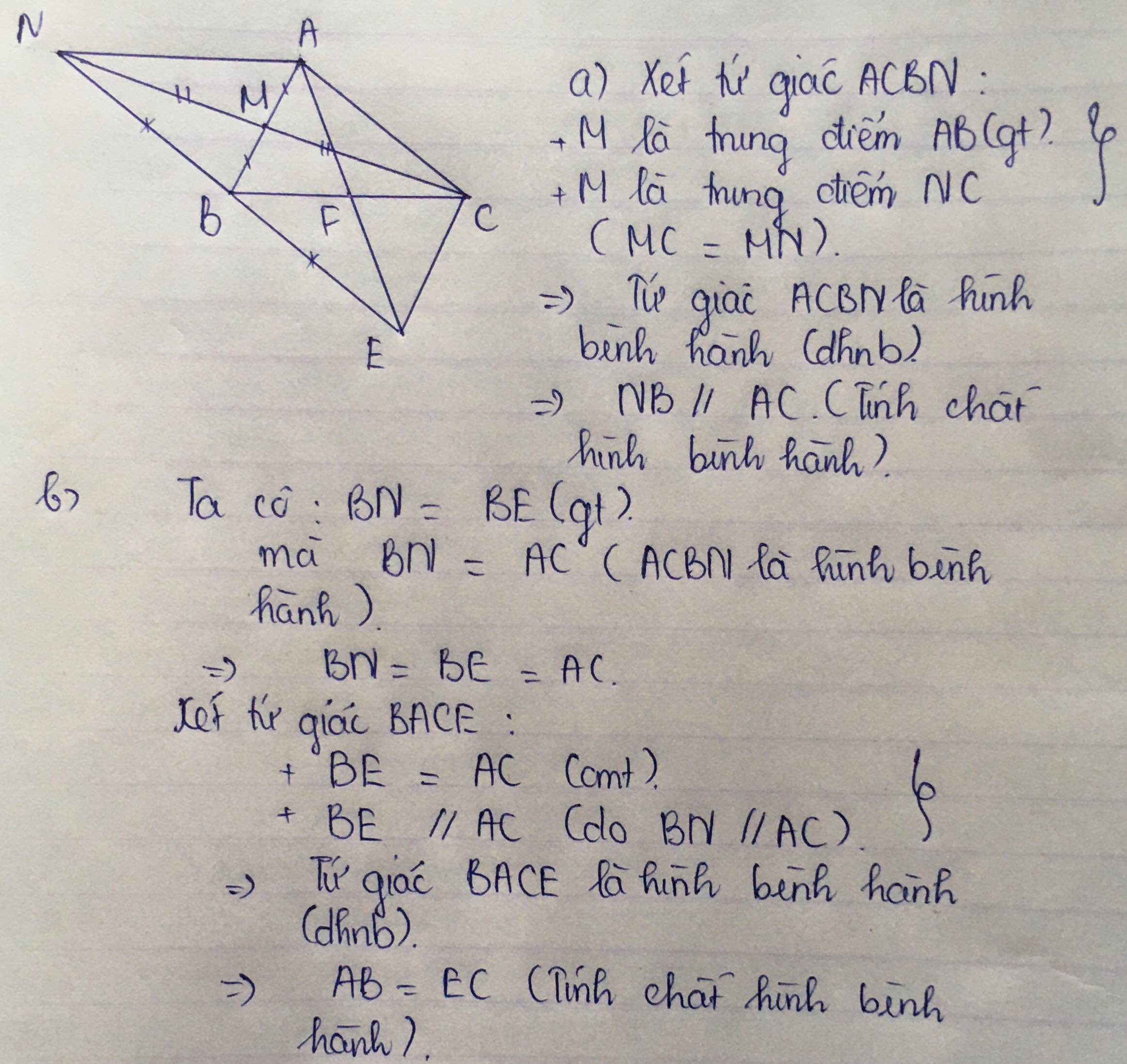
cho tam giác ABC,M là trung điểm của AB. Trên tia đối của tia MC lấy điểm N sao cho MC =MN
A. chứng minh rằng NB//AC
B. trên tia đối tia BN lấy điểm E sao cho BN=BE. Chứng minh: AB=EC
C. gọi F là trung điểm của BC. Chứng minh A,E,F thẳng hàng
tham khảo
mik ko thể vẽ hình đc
SORRY
Giải thích các bước giải:
a.*Xét ΔMBN,ΔMAC có:
MA=MB( vì M là trung điểm BA)
ˆNMB=ˆMC (2 góc đối đỉnh)
MN=MC
⇔ΔMNB=ΔMCA(c.g.c)
⇒ˆMNB=ˆMCA
⇒BN//AC
Vậy BN//AC
b.Từ câu a ⇒AC=BN
Ta có
BN//AC
⇒AC//BE
⇒ˆEAC=ˆAEB
*Xét ΔABE,ΔECA có:
AE chung
ˆAEB=ˆEAC
BE=AC
⇔ ΔABE=ΔECA(c.g.c)
⇒AB=EC
Vậy AB=EC
c.Ta có
AC//BE
⇒ˆACB=ˆCBE
⇒ˆACF=ˆFBE
*Xét ΔACF và ΔBEF có:
FB=FC( F là trung điểm của BC)
ˆACF=ˆEBF
AC=BE
⇔ΔACF=ΔEBF(c.g.c)
⇒ˆAFC=ˆBFE
⇒A,F,E thẳng hàng
Vậy A;F;E thẳng hàng
Đúng 0
Bình luận (1)
Cho tam giác ABC có AB = AC, trên cạnh BC lấy điểm M sao cho BM = MC.
a) Chứng minh
b) Chứng minh AM vuông góc với BC
c) Trên cạnh AC lấy điểm E sao cho AE = EC. Trên tia đối của tia EM vẽ điểm D sao cho E là trung điểm của đoạn MD. Chứng minh .
d) Chứng minh rằng DE=1/2.AB và DE//AB
e) Trên AD và MC lấy K và H sao cho AK = CH. Chứng minh Ba điểm K, E, H thẳng hàng
giúp mk câu d vs ! mk cảm ơn nhiều !
Bài 1. Cho ΔABC có trung tuyến AD (D BC) và phân giác trong BE (E AC). Dường thẳng qua E và song song với AD lần lượt cắt BC và AB tại M và N.a) Chứng minh rằng: MN . BD BM . AD.b) Chứng minh rằng: MN/AD + ME/AD 2.c) Chứng minh rằng: BC/BA MC/MDd) AD cắt BE tại I. Chứng minh rằng: IB/IE - BC/BA 1.Bài 2. Cho ΔABC (C 90°), có đường phân giác AD. Vẽ AE, CF, BN vuông góc với tia AD (F, N thuộc tia AD và E thuộc đường thẳng BC). Tia EF cắt cạnh AB tại I và cắt tia NB tại M. Chứng minh rằng:a) AB...
Đọc tiếp
Bài 1. Cho ΔABC có trung tuyến AD (D BC) và phân giác trong BE (E AC). Dường thẳng qua E và song song với AD lần lượt cắt BC và AB tại M và N.a) Chứng minh rằng: MN . BD = BM . AD.b) Chứng minh rằng: MN/AD + ME/AD = 2.c) Chứng minh rằng: BC/BA = MC/MDd) AD cắt BE tại I. Chứng minh rằng: IB/IE - BC/BA = 1.Bài 2. Cho ΔABC (C > 90°), có đường phân giác AD. Vẽ AE, CF, BN vuông góc với tia AD (F, N thuộc tia AD và E thuộc đường thẳng BC). Tia EF cắt cạnh AB tại I và cắt tia NB tại M. Chứng minh rằng:a) AB/AC = BN/FCb) AE là tia phân giác ngoài tại A của ΔABC. Từ đó suy ra EB/EC = AB/ACc) B là trung điểm của MN.d) ID FC.
Bài 1:
a: Xét ΔBNM có AD//NM
nên MN/AD=BM/BD
=>MN*BD=AD*BM
b: ME/AD=CM/CD=CM/BD
MN/AD+ME/AD=BM/BD+CM/BD=BC/BD=2
c:
Xét ΔBÂC có BE là phân giác
nen CE/CA=BC/BA
=>MC/MD=CE/CA=BC/BA
Đúng 0
Bình luận (0)
Cho tam giác ABC , M là trung điểm của AB . Trên tia đối của tia MC lấy điểm N sao cho MC= MN.
a. Chứng minh NB//AC
b. Trên tia đối BN lấy điểm E sao cho BN= BE. Chứng minh AB=EC.
c. Gọi F là trung điểm của BC. Chứng minh A, E , F thẳng hàng
a) Xét \(\Delta BNM\)và \(\Delta ACM\)có :
NM = MC ( gt )
\(\widehat{NMB}=\widehat{CMA}\)( hai góc đối đỉnh )
MB = MA ( gt )
Suy ra : \(\Delta BNM\)= \(\Delta ACM\)( c.g.c )
\(\Rightarrow NB=AC\)( hai cạnh tương ứng )
\(\Rightarrow\widehat{BNM}=\widehat{ACM}\)( hai góc tương ứng )
Mà hai góc này ở vị trí so le trong nên NB // AC
b) Xét \(\Delta BNC\)có \(\widehat{EBC}\)là góc ngoài nên \(\widehat{EBC}\)= \(\widehat{BNC}+\widehat{BCN}\)hay \(\widehat{EBC}\)= \(\widehat{ACM}+\widehat{BCN}=\widehat{ACB}\)
Xét \(\Delta BEC\)và \(\Delta BAC\)có :
BE = AC ( vì NB = BE = AC )
\(\widehat{EBC}\)= \(\widehat{ACB}\)( cmt )
BC ( cạnh chung )
Suy ra : \(\Delta BEC\)= \(\Delta BAC\)( c.g.c )
\(\Rightarrow AB=EC\)( hai cạnh tương ứng )
c) Vì \(\widehat{EFC}=\widehat{AFB}\)( hai góc đối đỉnh )
Mà \(\widehat{AFB}=180^o-\widehat{AFC}\)
\(\Rightarrow\widehat{EFC}+\widehat{AFC}=180^o-\widehat{AFC}+\widehat{AFC}=180^o\)
\(\Rightarrow\widehat{AFE}\)là góc bẹt nên A,F,E thẳng hàng
Đúng 0
Bình luận (0)
Tam giác ABC vuông tại A pg BM (M€ AC) trên BC lấy E sao BE=AB. a, cm tg BAM = tg BEM. F là giao của m và đường thẳng AB. b,Chứng minh FM = MC .c,chứng minh AM nhỏ hơn MC d,Chứng minh AE song song FC
Cho tam giác ABC; M, N lần lượt là trung điểm của AB, AC. a) Tứ giác BMNC là hình gì ? Vì sao ? b) Lấy điểm E đối xứng với M qua N. Chứng minh: AE // MC; BM = CE c) Gọi O là trung điểm của MC. Chứng minh rằng: Ba điểm B, O, E thẳng hàng.
a: Xét ΔABC có
M là trung điểm của AB
N là trung điểm của AC
Do đó: MN là đường trung bình của ΔABC
Suy ra: MN//BC
hay BMNC là hình thang
Đúng 0
Bình luận (0)
Cho △ABC nhọn (AB AC), gọi M là trung điểm của AB. Trên tia đối của tia MC, lấy điểm N sao cho MNMC. a) Chứng minh: △AMN △BMC và AC // BN. b) Gọi E, F lần lượt là trung điểm của AC, NB. Chứng minh: AF BE. c) Chứng minh: M là trung điểm FE.
Đọc tiếp
Cho △ABC nhọn (AB < AC), gọi M là trung điểm của AB. Trên tia đối của tia MC, lấy điểm N sao cho MN=MC.
a) Chứng minh: △AMN= △BMC và AC // BN.
b) Gọi E, F lần lượt là trung điểm của AC, NB. Chứng minh: AF = BE.
c) Chứng minh: M là trung điểm FE.
Chứng minh:
E=mc2
Ai đúng kb
Pương trình E=mc2 giải thích tại sao Uranium lại có thể liên tiếp, trong hàng triệu năm, bắn ra những tia li ti chạy với tốc độ khủng khiếp, tại sao mặt trời và các ngôi sao có thể tuôn ánh sáng và sức nóng trong hàng tỷ tỷ năm. Nó còn cho chúng ta thấy năng lượng ghê gớm chứa trong nhân nguyên tử và tiên đoán chỉ cần một lượng rất nhỏ Uranium cũng đủ tạo ra một trái bom có sức công phá hủy diệt cả một thành phố.
Đúng 0
Bình luận (0)