Cho đường thẳng a và b phân bieetjcungf vuông góc cới đường thẳng c thứ tự tại A và B. Một đường thẳng d cắt đường thẳng a tại D và cắt đường thẳng b tại C sao cho góc DCB=50 độ
a) Chứng minh đường thẳng a song song vớib
b) Tính góc ADC
Những câu hỏi liên quan
Câu 2: Cho hai đường thẳng a và b song song với nhau, đường thẳng c vuông góc với đt a tại A, vuông góc vớiđt b tại B. Đường thẳng d cắt đường thẳng a tại C và cắt đường thẳng b tại D. Biết ̂ACD=50° . Hãy vẽ hình, ghi GT-KL và tính số đo BDC
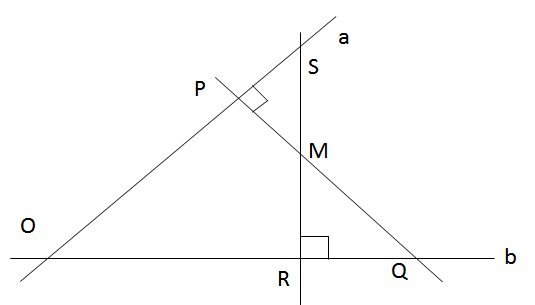
Cho hai đường thẳng phân biệt không song song a và b, điểm M nằm bên trong hai đường thẳng này. Qua M lần lượt vẽ đường thẳng c vuông góc với a tại P, cắt b tại Q và đường thẳng d vuông góc với b tại R, cắt a tại S. Chứng minh rằng đường thẳng qua M, vuông góc với SQ cũng đi qua giao điểm của a và b ?
(a) và (b) không song song nên (a) cắt (b), gọi giao điểm là O. Tam giác OSQ có PQ và RS là hai đường cao gặp nhau tại M nên M là trực tâm của tam giác nên đường thẳng vẽ từ M và vuông góc với SQ là đường cao thứ ba của tam giác tức là đường vuông góc với SQ vẽ từ M cũng đi qua giao điểm của a và b
Đúng 0
Bình luận (0)
(a) và (b) không song song nên (a) cắt (b), gọi giao điểm là O. Tam giác OSQ có PQ và RS là hai đường cao gặp nhau tại M nên M là trực tâm của tam giác nên đường thẳng vẽ từ M và vuông góc với SQ là đường cao thứ ba của tam giác tức là đường vuông góc với SQ vẽ từ M cũng đi qua giao điểm của a và b
Đúng 0
Bình luận (0)
Vì a và b không song song nên chúng cắt nhau giả sử tại A.
Xét ΔAQS có:
QP ⊥ AS (vì QP ⊥ a)
SR ⊥ AQ (vì SR ⊥ b)
Ta có QP và RS cắt nhau tại M. Vậy M là trực tâm của ΔAQS.
=> Đường thẳng đi qua M và vuông góc với QS tại H sẽ là đường cao thứ ba của ΔAQS.
Vậy MH phải đi qua đỉnh A của ΔAQS hay đường thẳng vuông góc với QS đi qua giao điểm của a và b (đpcm).
Đúng 0
Bình luận (0)
Cho hai đường thẳng phân biệt không song song a và b, điểm M nằm bên trong hai đường thẳng này. Qua M lần lượt vẽ đường thẳng c vuông góc với a tại P, cắt b tại Q và đường thẳng d vuông góc với b tại R, cắt a tại S. Chứng minh rằng đường thẳng qua M, vuông góc với SQ cũng đi qua giao điểm của a và b.
Gọi A là giao điểm của a và b.
Theo giả thiết c ⟘ a hay SR ⟘ AQ hay SR là đường cao của ΔASQ.
d ⟘ b hay PQ ⟘ AS hay QP là đường cao của ΔASQ.
SR cắt QP tại M ⇒ M là trực tâm của ΔASQ
⇒ AM ⟘ SQ
Vậy đường thẳng đi qua M và vuông góc với SQ cũng đi qua A (đpcm).
Đúng 0
Bình luận (0)
Cho hai đường thẳng phân biệt không song song a và b, điểm M nằm bên trong hai đường thẳng này. Qua M lần lượt vẽ đường thẳng c vuông góc với a tại P, cắt b tại Q và đường thẳng d vuông góc với b tại R, cắt a tại S. Chứng minh rằng đường thẳng qua M, vuông góc với SQ cũng đi qua giao điểm của a và b.
Cho ΔABC cân tại A. Đường thẳng vuông góc với AB tại B cắt đường thẳng vuông góc với AC tại C ở D; M là trung điểm BC.a) Chứng minh: AD là phân giác của và A, M, D thẳng hàng. b) Qua B kẻ đường thẳng vuông góc AC cắt AC tại K, cắt AD tại I. Chứng minh: BC là đường trung trực của ID.
Đọc tiếp
Cho ΔABC cân tại A. Đường thẳng vuông góc với AB tại B cắt đường thẳng vuông góc với AC tại C ở D; M là trung điểm BC.
a) Chứng minh: AD là phân giác của 
b) Qua B kẻ đường thẳng vuông góc AC cắt AC tại K, cắt AD tại I. Chứng minh: BC là đường trung trực của ID.
a) Xét ΔABD vuông tại B và ΔACD vuông tại C có
AD chung
AB=AC(ΔABC cân tại A)
Do đó: ΔABD=ΔACD(Cạnh huyền-cạnh góc vuông)
Suy ra: \(\widehat{BAD}=\widehat{CAD}\)(hai góc tương ứng)
mà tia AD nằm giữa hai tia AB,AC
nên AD là tia phân giác của \(\widehat{BAC}\)(đpcm)
Ta có: ΔABD=ΔACD(cmt)
nên DB=DC(hai cạnh tương ứng)
Ta có: DB=DC(cmt)
nên D nằm trên đường trung trực của BC(Tính chất đường trung trực của một đoạn thẳng)(1)
Ta có: AB=AC(ΔABC cân tại A)
nên A nằm trên đường trung trực của BC(Tính chất đường trung trực của một đoạn thẳng)(2)
Ta có: MB=MC(M là trung điểm của BC)
nên M nằm trên đường trung trực của BC(Tính chất đường trung trực của một đoạn thẳng)(3)
Từ (1), (2) và (3) suy ra A,M,D thẳng hàng(đpcm)
Đúng 1
Bình luận (0)
Cho đường tròn (O; R), một điểm A nằm ngoài đường tròn, một đường thẳng d vuông góc với OA tại A, đường thẳng OA cắt (O) tại B và C (B nằm giữa O và A). Từ C vẽ tia Cx cắt (O) tại D và cắt d tại E.
a) Chứng minh rằng CB.CA = CD.CE
b) Cho ACE=30 độ , OA = 2R. Tính CE và AE theo R
Cho đường tròn (O) đường kính BC , A là một điểm thuộc (O) sao cho AB < AC , D là điểm giữa O và C . Đường thẳng vuông góc với BC tại D cắt AC tại E và cắt đường thẳng BE tại F a, Chứng minh tứ giác ABDE và ADCF nội tiếp b, Chứng minh góc AEF = góc ABC c, Tiếp tuyến tại A của (O) cắt DE tại M . Chứng minh tam giác AME cân tại M
a: góc BAC=1/2*sđ cung BC=90 độ
Vì góc BAE+góc BDE=180 độ
=>BAED nội tiếp
góc CAF=góc CDF=90 độ
=>CFAD nội tiếp
b: góc AEF+góc AFE=90 dộ
góc ABC+góc ACB=90 độ
mà góc AFE=góc ACB(=90 độ-góc B)
nên góc AEF=góc ABC
c: góc MAE=1/2*sđ cung AC
góc MEA=góc DEC=90 độ-góc ACB=góc ABC=1/2*sđ cung AC
=>góc MAE=góc MEA
=>ΔMAE cân tại M
Đúng 0
Bình luận (0)
Cho đường tròn (O) đường kính BC , A là một điểm thuộc (O) sao cho AB < AC , D là điểm giữa O và C . Đường thẳng vuông góc với BC tại D cắt AC tại E và cắt đường thẳng BE tại F a, Chứng minh tứ giác ABDE và ADCF nội tiếp b, Chứng minh góc AEF = góc ABC c, Tiếp tuyến tại A của (O) cắt DE tại M . Chứng minh tam giác AME cân tại M
a: góc BAC=1/2*sđ cung BC=90 độ
Vì góc BAE+góc BDE=180 độ
=>BAED nội tiếp
góc CAF=góc CDF=90 độ
=>CFAD nội tiếp
b: góc AEF+góc AFE=90 dộ
góc ABC+góc ACB=90 độ
mà góc AFE=góc ACB(=90 độ-góc B)
nên góc AEF=góc ABC
Đúng 0
Bình luận (0)
cho tam giác abc có các phân giác ngoài ở đỉnh b và c cắt nhau tại k
a) chứng minh ak là phân giác của góc A
b)qua C kẻ đường thẳng vuông góc với CK cắt AK tại I. Qua A kẻ đường thẳng d vuông góc với AK. Chứng minh 3 đường thẳng d; BI; CK đồng qui
c) Hai đường thẳng d và BK cắt nhau tại H. Chứng minh 3 điểm H,I,C thẳng hàng
tích mình đi
ai tích mình
mình tích lại
thanks
Đúng 0
Bình luận (0)