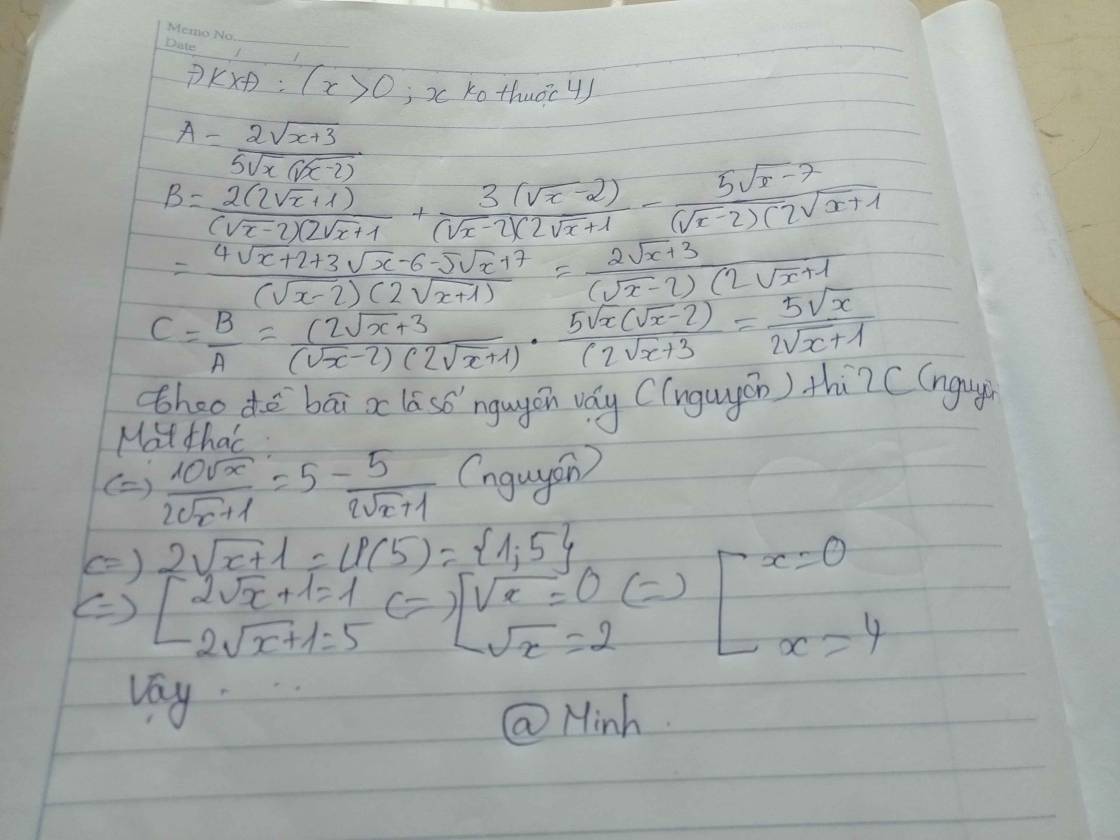Cho M= \(\sqrt{x^2-5x+14}-\sqrt{x^2-5x+10}\)=0. Tính giá trị biểu thức liên hợp của vế phải

Những câu hỏi liên quan
Bài 1 : Cho \(\sqrt{x^2-5x+14}+\sqrt{x^2-5x+10}=2\) Tính giá trị biểu thức M = \(\sqrt{x^2-5x+10}+\sqrt{x^2-5x+10}\)
Bài 2 : Tìm GTNN của : Q = \(\sqrt{x^2+4x+4}+\sqrt{x^2-4x+4}\)
Bài 1 : Cho biểu thức R left[frac{2sqrt{x}}{sqrt{x}+3}+frac{sqrt{x}}{sqrt{x}-3}-frac{3cdotleft(sqrt{x}+3right)}{x-9}right]:left(frac{2sqrt{x}-2}{sqrt{x}-3}-1right)a/ Rút gọn Rb/ Tìm các giá trị của x để R -1Bài 2 : Cho sqrt{x^2-5x+14}-sqrt{x^2-5x+10}2Tính giá trị biểu thức M sqrt{x^2-5x+14}+sqrt{x^2-5x+10}Bài 3 : Tìm GTNN của : Q sqrt{x^2+4x+4}+sqrt{x^2-4x+4}
Đọc tiếp
Bài 1 : Cho biểu thức R = \(\left[\frac{2\sqrt{x}}{\sqrt{x}+3}+\frac{\sqrt{x}}{\sqrt{x}-3}-\frac{3\cdot\left(\sqrt{x}+3\right)}{x-9}\right]:\left(\frac{2\sqrt{x}-2}{\sqrt{x}-3}-1\right)\)
a/ Rút gọn R
b/ Tìm các giá trị của x để R < -1
Bài 2 : Cho \(\sqrt{x^2-5x+14}-\sqrt{x^2-5x+10}=2\)Tính giá trị biểu thức M =\(\sqrt{x^2-5x+14}+\sqrt{x^2-5x+10}\)
Bài 3 : Tìm GTNN của : Q = \(\sqrt{x^2+4x+4}+\sqrt{x^2-4x+4}\)
\(R=\left[\frac{2\sqrt{x}}{\sqrt{x}+3}+\frac{\sqrt{x}}{\sqrt{x}-3}-\frac{3\left(\sqrt{x}+3\right)}{x-9}\right]:\left(\frac{2\sqrt{x}-2}{\sqrt{x}-3}-1\right)\)
a/ \(R=\left[\frac{2\sqrt{x}}{\sqrt{x}+3}+\frac{\sqrt{x}}{\sqrt{x}-3}-\frac{3\left(\sqrt{x}+3\right)}{\left(\sqrt{x}+3\right)\left(\sqrt[]{x-3}\right)}\right]:\left(\frac{2\sqrt{x}-2-\sqrt{x}+3}{\sqrt{x}-3}\right)\)
=> \(R=\left[\frac{2\sqrt{x}}{\sqrt{x}+3}+\frac{\sqrt{x}}{\sqrt{x}-3}-\frac{3}{\sqrt[]{x-3}}\right]:\frac{\sqrt{x}+1}{\sqrt{x}-3}\)
=> \(R=\left[\frac{2\sqrt{x}}{\sqrt{x}-3}+1\right]:\frac{\sqrt{x}+1}{\sqrt{x}-3}\)
=> \(R=\left[\frac{2\sqrt{x}+\sqrt{x}-3}{\sqrt{x}-3}\right].\frac{\sqrt{x}-3}{\sqrt{x}+1}\)
=> \(R=\frac{3\sqrt{x}-3}{\sqrt{x}-3}.\frac{\sqrt{x}-3}{\sqrt{x}+1}=\frac{3\left(\sqrt{x}-1\right)}{\sqrt{x}+1}\)
b/ Để R<-1 => \(\frac{3\left(\sqrt{x}-1\right)}{\sqrt{x}+1}< -1\)
<=> \(3\sqrt{x}-3< -\sqrt{x}-1\)
<=> \(4\sqrt{x}< 2\)=> \(\sqrt{x}< \frac{1}{2}\) => \(-\frac{1}{4}< x< \frac{1}{4}\)
Đúng 0
Bình luận (0)
Chỗ => R = \(\left(\frac{2\sqrt{x}}{\sqrt{x}-3}+1\right):\frac{\sqrt{x}+1}{\sqrt{x}-3}\) là sao vậy ạ?
Đúng 0
Bình luận (0)
Thì \(\frac{\sqrt{x}}{\sqrt{x}-3}-\frac{3}{\sqrt{x}-3}=\frac{\sqrt{x}-3}{\sqrt{x}-3}=1\)
Đúng 0
Bình luận (0)
Cho biểu thức \(\sqrt{x^2-5x+14}-\sqrt{x^2-5x+10}=2\). Tính \(A=\sqrt{x^2-5x+14}+\sqrt{x^2-5x+10}\)
ta có
\(2A=\left(\sqrt{x^2-5x+14}-\sqrt{x^2-5x+10}\right)\left(\sqrt{x^2-5x+14}+\sqrt{x^2-5x+10}\right)\)
⇔ 2A=x2-5x+14-x2+5x-10
⇔2A= 4
⇔ A=2
Đúng 0
Bình luận (0)
Tìm giá trị nhỏ nhất của
M = \(\sqrt{x^2-5x+14}+\sqrt{x^2-5x+10}\)
Giải các phương trình sau bằng phương pháp nhân thêm lượng liên hợp.
a) \(\sqrt{3x+1}+2x=\sqrt{x-4}-5;\)
b) \(\sqrt{3x+5}+x=6+\sqrt{2x+11};\)
c) \(\sqrt{x^2+5x+5}+x^2=\sqrt{x+2}-3x-2.\)
a)\(\sqrt{3x+1}+2x=\sqrt{x-4}-5\left(ĐKXĐ:x\ge4\right)\)
\(\Leftrightarrow\left(\sqrt{3x+1}-\sqrt{x-4}\right)+\left(2x+5\right)=0\)
\(\Leftrightarrow\frac{3x+1-x+4}{\sqrt{3x+1}+\sqrt{x-4}}+\left(2x+5\right)=0\)
\(\Leftrightarrow\frac{2x+5}{\sqrt{3x+1}+\sqrt{x-4}}+\left(2x+5\right)=0\)
\(\Leftrightarrow\left(2x+5\right)\left(\frac{1}{\sqrt{3x+1}+\sqrt{x-4}}+1\right)=0\)
a') (tiếp)
\(\Leftrightarrow\orbr{\begin{cases}2x+5=0\\\frac{1}{\sqrt{3x+1}+\sqrt{x-4}}+1=0\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=-2,5\left(KTMĐKXĐ\right)\\\frac{1}{\sqrt{3x+1}+\sqrt{x-4}}+1=0\end{cases}}\)
Xét phương trình \(\frac{1}{\sqrt{3x+1}+\sqrt{x-4}}+1=0\)(1)
Với mọi \(x\ge4\), ta có:
\(\sqrt{3x+1}>0\); \(\sqrt{x-4}\ge0\)
\(\Rightarrow\sqrt{3x+1}+\sqrt{x-4}>0\Rightarrow\frac{1}{\sqrt{3x+1}+\sqrt{x-4}}>0\)
\(\Rightarrow\frac{1}{\sqrt{3x+1}+\sqrt{x-4}}+1>0\)
Do đó phương trình (1) vô nghiệm.
Vậy phương trình đã cho vô nghiệm.
b) \(\sqrt{3x+5}+x=6+\sqrt{2x+11}\left(ĐKXĐ:x\ge-\frac{5}{3}\right)\)\(\Leftrightarrow\left(\sqrt{3x+5}-\sqrt{2x+11}\right)+\left(x-6\right)=0\)
\(\Leftrightarrow\frac{3x+5-2x-11}{\sqrt{3x+5}+\sqrt{2x+11}}+\left(x-6\right)=0\)
\(\Leftrightarrow\frac{x-6}{\sqrt{3x+5}+\sqrt{2x+11}}+\left(x-6\right)=0\).
\(\Leftrightarrow\left(x-6\right)\left(\frac{1}{\sqrt{3x+5}+\sqrt{2x+11}}+1\right)=0\)
Xem thêm câu trả lời
Cho \(\sqrt{x^2-5x+14}-\sqrt{x-5x+10}=2\)
Tính \(M=\sqrt{x^2-5x+14}+\sqrt{x^2-5x+10}\)
Đặt \(\sqrt{x^2-5x+14}=a\) và \(\sqrt{x^2-5x+10}=b\) \(\left(a,b>0\right)\)
\(\Rightarrow a-b=2\)
\(\Rightarrow a^2-b^2=x^2-5x+14-x^2+5x-10=4\)
\(\Leftrightarrow\left(a-b\right)\left(a+b\right)=4\)
\(\Leftrightarrow a-b=2\)
\(\Leftrightarrow\sqrt{x^2-5x+14}+\sqrt{x^2-5x+10}=2\left(đpcm\right)\)
Đúng 0
Bình luận (0)
CHO BIỂU THỨC A=\(\left(\frac{2}{\sqrt{x}-2}+\frac{3}{2\sqrt{x}+1}-\frac{5\sqrt{x}-7}{2x-3\sqrt{x}-2}\right):\frac{2\sqrt{x}+3}{5x-10\sqrt{x}}\left(x>0;x#4\right)\) X#4)
1, tính giá trị của A khi x=\(3-2\sqrt{2}\)
2. tìm x sao cho A nhận giá trị là một số nguyên
Giúp em với:
Cho: \(\sqrt{x^2-5x+14}-\sqrt{x^2-5x+10}=2\)
Tính: M= \(\sqrt{x^2-5x+14}+\sqrt{x^2-5x+10}\)
Ta có
(\(\sqrt{x^2-5x+14}+\sqrt{x^2-5x+10}\))(\(\sqrt{x^2-5x+14}-\sqrt{x^2-5x+10}\)) = 4
=> M = 2
Đúng 0
Bình luận (0)
em ngố vậy nhân hai cái với nhau là được mà
Đúng 0
Bình luận (0)
Châu nói gì mà kì vậy? Nói thì nói mà có biết giải ko??
Đúng 0
Bình luận (0)
Cho hai biểu thức \(A=\dfrac{2\sqrt{x}+3}{5x-10\sqrt{x}}\) và \(B=\dfrac{2}{\sqrt{x}-2}+\dfrac{3}{2\sqrt{x}+1}-\dfrac{5\sqrt{x}-7}{2x-3\sqrt{x}-2}\) với x>0, x≠4. Tìm x sao cho \(\dfrac{B}{A}\)nhận giá trị là một số nguyên.