\(x-y=xy-1\)

\(\Rightarrow x-y-xy+1=0\)

\(\Rightarrow x\left(1-y\right)+\left(1-y\right)=0\)

\(\Rightarrow\left(x+1\right)\left(1-y\right)=0\)

+) Với $x=-1$ thì ta có mọi $y$ thỏa mãn

+) Với $y=1$ thì ta có mọi $x$ thỏa mãn.

Bài 1:

Thay \(x\) = 6y vào biểu thức ta có:

|6y| - |y| = 60

|5y| = 60

5.|y| = 60

   |y| = 60 : 5

   |y| = 12

   \(\left[{}\begin{matrix}y=-12\\y=12\end{matrix}\right.\)

⇒ \(\left[{}\begin{matrix}x=-72\\x=72\end{matrix}\right.\)

Kết luận:

Các cặp \(x;y\) nguyên thỏa mãn đề bài là:

(\(x;y\)) = (-72; -12); (72; 12)

\(a,\Leftrightarrow y\left(x+1\right)-3\left(x+1\right)=5\\ \Leftrightarrow\left(x+1\right)\left(y-3\right)=5=5.1=\left(-5\right)\left(-1\right)\\ TH_1:\left\{{}\begin{matrix}x+1=1\\y-3=5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=0\\y=8\end{matrix}\right.\\ TH_2:\left\{{}\begin{matrix}x+1=5\\y-3=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=4\\y=4\end{matrix}\right.\\ TH_3:\left\{{}\begin{matrix}x+1=-5\\y-3=-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-6\\y=2\end{matrix}\right.\\ TH_4:\left\{{}\begin{matrix}x+1=-1\\y-3=-5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-2\\y=-2\end{matrix}\right.\)

Vậy \(\left(x;y\right)\in\left\{\left(0;8\right);\left(4;4\right);\left(-6;2\right);\left(-2;-2\right)\right\}\)

\(b,\Leftrightarrow6\left(n-1\right)+11⋮n-1\\ \Leftrightarrow n-1\in\left\{-11;-1;1;11\right\}\\ \Leftrightarrow n\in\left\{-10;0;2;12\right\}\)

x-y=xy-1

<=> x-y-xy+1=0

<=> x(1-y) + (1-y)=0

<=> (x+1)(y-1)=0

x=-1 hoặc y=1

Vậy (x,y) = (-1, y thuộc Z )

hoặc (x,y)=( x thuộc Z , y=1)

Chúc bạn học tốt .

bài 1:

a)<=>(n-1)+4 chia hết n-1

=>4 chia hết n-1

=>n-1\(\in\){-1,-2,-4;1,2,4}

=>n\(\in\){0,-1,-3,2,3,5}

b)<=>2(2n+1)+2 chia hết 2n+1

=>4 chia hết 2n+1

=>2n+1\(\in\){-1,-2,-4,1,2,4}

=>n\(\in\){-1;-3;-7;3;5;9}

bài 3 : <=>2y+8+xy+4x-1y-4=11

=>(8-4)+(2y-1y)+xy+4x=11

=>4+1y+x.y+x.4=11

=>1y+x.(x+y)=11-4

=>y+x.x+y=8

=>(x+y)^2=8

=>x+y=3

=>x và y là các số có tổng =3 ( bn tự liệt kê nhé )

Lời giải:
a. $(x-3)(y+1)=5=1.5=5.1=(-1)(-5)=(-5)(-1)$
Vì $x-3, y+1$ cũng là số nguyên nên ta có bảng sau:

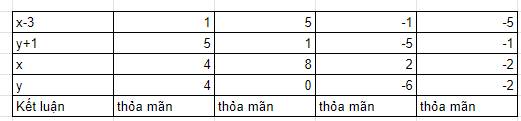
b.

$A=21+5+(5^2+5^3)+(5^4+5^5)+....+(5^{98}+5^{99})$

$=26+5^2(1+5)+5^4(1+5)+....+5^{98}(1+5)$

$=2+24+(1+5)(5^2+5^4+...+5^{98}$

$=2+24+6(5^2+5^4+....+5^{98})=2+6(4+5^2+5^4+...+5^{98})$

$\Rightarrow A$ chia $6$ dư $2$.

Bài 2: Giả sử tồn tại x,y nguyên dương t/m đề, khi đó pt cho tương đương:

\(4x^2+4y^2-12x-12y=0\Leftrightarrow\left(2x+3\right)^2+\left(2y+3\right)^2=18\)

Ta thấy: \(18=9+9=3^2+3^2\). Mà x,y thuộc Z⁺ nên \(\hept{\begin{cases}2x+3=3\\2y+3=3\end{cases}\Leftrightarrow}\hept{\begin{cases}x=0\\y=0\end{cases}}\)

Vậy cặp nghiệm nguyên t/m pt là (x;y) = (0;0)

Làm lại bài 2 :v (P/S: Bạn bỏ bài kia đi nhé)

\(4x^2+4y^2-12x-12y=0\Leftrightarrow\left(2x-3\right)^2+\left(2y-3\right)^2=18\)

Ta thấy: \(18=9+9=3^2+3^2\). Mà x,y thuộc Z⁺ nên \(\hept{\begin{cases}2x-3=3\\2y-3=3\end{cases}\Leftrightarrow}\hept{\begin{cases}x=3\\y=3\end{cases}}\)

Vậy (x;y) = (3;3)

Bây giờ cậu cần không thế;D

h mik ko gấp nữa, nhưng nếu cậu biết cách giải thì chỉ mik nha ạ, làm tư liệu sau này mik học ý ạ :>

số cặp x,y là : 

N :2 = ??

đ/s:.......

số cặp x,y,z là :

N^* :3=?

sai rồi

1. \(\frac{x}{y}=\frac{7}{17}\)

3. Có 6 cặp

4. 0 có cặp nào hết

Câu 2 mình không biết nha. Thông cảm