cho 2 đường thẳng AB song song với CD lấy M thuộc AB; N thuộc CD sao cho 2 tia MB và ND thuộc cùng 1 nửa mặt phẳng bờ MN vẽ tia Mx ở trong góc AMN vẽ tia MY trên nửa mặt phẳng bờ CD ko chứa M sao cho góc AMX=CMY chứng minh mx song song với NY

Những câu hỏi liên quan
cho 2 đường thẳng AB song song với CD lấy M thuộc AB; N thuộc CD sao cho 2 tia MB và ND thuộc cùng 1 nửa mặt phẳng bờ MN vẽ tia MX ở trong góc AMN vẽ tia NY trên mặt phẳng bờ CD không chứa M sao cho góc ÃM=CMY chứng minh MX song song NY
Dpcm ANx // CNy
do AB//CD nen
=>AM // CM va MB//ND
=>AMB // CND
=>ANx // CNy
Đúng 0
Bình luận (0)
a). Ta có: góc AMx=góc B (GT)
Mà góc AMx và góc B là hai góc đồng vị.
=> Mx//BC.
Kéo dài tia Mx, cắt CD tại E.
Vì AB//CD(gt) nên AMEˆ=DEMˆ(slt)AME^=DEM^(slt)
mà theo gt AMEˆ=CNyˆAME^=CNy^ nên DEMˆ=CNyˆDEM^=CNy^
=> Mx//Ny(do có 1 cặp góc bằng nhau ở vị trí so le trong
Đúng 0
Bình luận (0)
Cho 2 đường thẳng ab và cd song song với nhau. Lấy M thuộc ab,N thuộc cd sao cho hai tia Mb và Nd cùng thuộc một nửa mặt phẳng bMN. Vẽ tia Mx ở trong góc aMN, tia Ny trên nửa mặt phẳng bờ cd không chứa M sao cho góc aMx=cNy. Chứng minh Mx song song với Ny
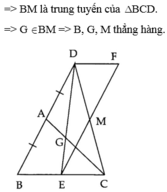
Cho tam giác ABC, trên tia đối của AB lấy D sao cho AD=AB. Lấy G thuộc AC sao cho AG = 1/3.AC. Tia DG cắt BC tại E; qua E vẽ đường thẳng song song với BD; qua D vẽ đường thẳng song song với BC. Hai đường này cắt nhau tại F. Gọi M là giao của È và CD. Chứng minh 3 điểm B, G, M thẳng hàng.
cho hai đường thẳng AB và CD song song với nhau. Lấy M thuộc AB, N thuộc CD sao cho hai tia MB và ND thuộc cùng một nửa mặt phẳng bờ MN. Vẽ tia Mx trong góc AMN, vẽ tia Ny trên nửa mặt phẳng bờ CD không chứa M sao cho góc AMx = góc CNy. CMR: Mx//Ny
Cho 2 đường thẳng AB và CD song song vs nhau. Lấy M thuộc AB, N thuộc CD sao cho 2 tia MB và ND cùng thuộc nửa mặt phẳng có bờ MN. Vẽ tia Mx ở trong góc AMN. Vẽ tia NY trên nửa mặt phẳng có bở ko chứa điểm M sao cho:
AMx = CNy. Chửng minh rằng Mx song song với Ny
do AB//CD nen
=>AM // CM va MB//ND
=>AMB // CND
=>ANx // CNy
Đúng 0
Bình luận (0)
Vì AB//CD
=>AM//CM;MB//ND
=>AMB//CND
=>ANx//CNy
Vậy ANx//CNy
Đúng 0
Bình luận (0)
cho tam giác ABC. lấy D thuộc AB và E thuộc BC. Đường thẳng qua D song song BC cắt AE ở G và AC tại I. Đường thẳng qua E song song với AB cắt CD ở F.
1) so sánh GD/AB và EB/EC. 2) Chứng minh GF//AC
Cho tam giác ABC, trên tia đối của AB lấy D sao cho AD=AB. Lấy G thuộc AC sao cho AG = 1/3.AC. Tia DG cắt BC tại E; qua E vẽ đường thẳng song song với BD; qua D vẽ đường thẳng song song với BC. Hai đường này cắt nhau tại F. Gọi M là giao của È và CD. Chứng minh 3 điểm B, G, M thẳng hàng.
Ta có:AB=AD
=>AC là đường trung tuyến
Mà AG=\(\frac{1}{3}\)AC nên:
=>G là trọng tâm
Ta có:tia DE cắt BC tại E nên:
=>DE là đường trung tuyến
=>BE=EC
Xét ΔDBE và ΔDEF có:
góc D1=góc D2 (so le trong) (DB//EF)
DE cạnh chung
góc FDG=góc E1 (so le trong)
=>ΔDBE=ΔDEF(g.c.g)
=>BE=DF(2 cạnh tương ứng)
Mà BE=EC nên EC=DF
Xét ΔDEM và ΔEMC có:
góc D3=góc C(so le trong) (DF//BE)
góc F=góc E3(so le trong) (DF//BE)
EC=DF (cmt)
=>ΔDEM=ΔEMC (g.c.g)
=>DM=MC (2 cạnh tương ứng)
=>BM là đường trung tuyến
=>B,G,M thẳng hàng
CHÚC BN HC TỐT!!!^^
Đúng 0
Bình luận (0)
Cho tam giác ABC. Trên tia đối của tia AB lấy điểm D sao cho AD AB. Lấy G thuộc cạnh AC sao cho
A
G
1
3
A
C
. Tia DG cắt BC tại E. Qua E vẽ đường thẳng song song với BD, qua D vẽ đường thẳng song song với BC, hai đường thẳng này cắt nhau tại F. Gọi M là giao điểm của EF và CD.Chứng minh:a) G là trọng tâm tam giác BCD;b)
∆
B
E
D
∆...
Đọc tiếp
Cho tam giác ABC. Trên tia đối của tia AB lấy điểm D sao cho AD = AB. Lấy G thuộc cạnh AC sao cho A G = 1 3 A C . Tia DG cắt BC tại E. Qua E vẽ đường thẳng song song với BD, qua D vẽ đường thẳng song song với BC, hai đường thẳng này cắt nhau tại F. Gọi M là giao điểm của EF và CD.
Chứng minh:
a) G là trọng tâm tam giác BCD;
b) ∆ B E D = ∆ F D E , từ đó suy ra EC = DF;
c) ∆ D M F = ∆ C M E ;
d) B, G, M thẳng hàng.
Cho đường tròn tâm O, đường kính CD, dây AB vuông góc với CD, AB = R căn 3, C thuộc cung AB lớn. Trên cung AC lấy M, kẻ AN song song với CN. Tính MN