Giúp vs m. N 

Vì a⊥c và b⊥c nên a//b

Do đó \(x+y=180^0\)

Áp dụng tc dtsbn:

\(\dfrac{x}{y}=\dfrac{3}{2}\Rightarrow\dfrac{x}{3}=\dfrac{y}{2}=\dfrac{x+y}{3+2}=\dfrac{180^0}{5}=36^0\\ \Rightarrow\left\{{}\begin{matrix}x=108^0\\y=72^0\end{matrix}\right.\)

Đang cần gấp ạ giúp đúng mik tích ạ 

B1:
a.(-14/39)
b.45 độ
B2:
a.x=(-13/10)
b.
c.0

Bài 1:

a/\(\dfrac{17}{3}-\dfrac{5}{3}=\dfrac{17-5}{3}=\dfrac{12}{3}\)=4

b/Tam giác ABC có:

góc A+góc B+góc C=180 độ

=>70 độ+65 độ+góc C=180 độ

=>góc C =180 độ-70 độ-65 độ=45 độ

Bài 2:

a/\(x+3\dfrac{1}{2}=\dfrac{11}{5}=>x+\dfrac{7}{2}=\dfrac{11}{5}=>x=\dfrac{11}{5}-\dfrac{7}{2}=\dfrac{-13}{10}\)

c/\(\left(\dfrac{-3}{7}+\dfrac{5}{11}\right):\dfrac{4}{31}+\left(\dfrac{-4}{7}+\dfrac{6}{11}\right):\dfrac{4}{31}\)

=>\(\left(\dfrac{-3}{7}+\dfrac{5}{11}\right).\dfrac{31}{4}+\left(\dfrac{-4}{7}+\dfrac{6}{11}\right).\dfrac{31}{4}\)

=>\(\dfrac{31}{4}.\left(\dfrac{-3}{7}+\dfrac{5}{11}+\dfrac{\left(-4\right)}{7}+\dfrac{6}{11}\right)=\dfrac{31}{4}.0=0\)

hình đâu

a.

\(y'=\dfrac{\left(sinx+cosx\right)'}{2\sqrt{sinx+cosx}}=\dfrac{cosx-sinx}{2\sqrt{sinx+cosx}}\)

b.

\(y'=\dfrac{-4}{\left(x-1\right)^2}\)

Tiếp tuyến vuông góc với \(y=\dfrac{1}{4}x+5\) nên có hệ số góc thỏa mãn \(k.\left(\dfrac{1}{4}\right)=-1\Rightarrow k=-4\)

\(\Rightarrow\dfrac{-4}{\left(x-1\right)^2}=-4\Rightarrow\left(x-1\right)^2=1\)

\(\Rightarrow\left[{}\begin{matrix}x=0\Rightarrow y=-3\\x=2\Rightarrow y=5\end{matrix}\right.\)

Có 2 tiếp tuyến thỏa mãn: \(\left[{}\begin{matrix}y=-4x-3\\y=-4\left(x-2\right)+5\end{matrix}\right.\)

thiếu đề 

Đề thế này thì có ma trả lời.

ta có góc A3= B4=60 độ( trong cùng phía bù nhau)

lại có A2=A3= 60 độ (đối đỉnh)

vậy góc A2= 60 độ

Toi cần đc giải cứu

a) Xét ΔABC vuông tại A có \(\widehat{C}=30^0\)(gt)

mà cạnh đối diện với \(\widehat{C}\)

nên \(\dfrac{AB}{BC}=\dfrac{1}{2}\)(Định lí)

Xét ΔABC có BD là đường phân giác ứng với cạnh AC(gt)

nên \(\dfrac{AD}{CD}=\dfrac{AB}{BC}\)(Tính chất tia phân giác của tam giác)

hay \(\dfrac{AD}{CD}=\dfrac{1}{2}\)

b) Ta có: \(BC=2\cdot AB\)(cmt)

nên \(BC=2\cdot12.5=25\left(cm\right)\)

Áp dụng định lí Pytago vào ΔBAC vuông tại A, ta được:

\(BC^2=AB^2+AC^2\)

\(\Leftrightarrow AC^2=BC^2-AB^2=25^2-12.5^2=468.75\)

hay \(AC=\dfrac{25\sqrt{3}}{2}cm\)

Diện tích tam giác ABC là:

\(S_{ABC}=\dfrac{AB\cdot AC}{2}=\dfrac{12\cdot\dfrac{25\sqrt{3}}{2}}{2}=\dfrac{150\sqrt{3}}{2}=75\sqrt{3}\left(cm^2\right)\)

a: a⊥c

b⊥c

Do đó: a//b

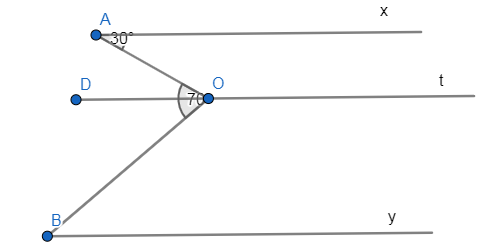
a, Kẻ Ot sao cho Ot song song với Ax và By, ta có:

\(\widehat{xAO}=\widehat{AOD}\) (So le trong)

\(\Rightarrow\widehat{xAO}=\widehat{AOD}=30^0\\\Rightarrow\widehat{DOB}=70^0-30^0=40^0\)

Mà OD//By

\(\Rightarrow\widehat{B}=\widehat{DOB}=40^0\)