vẽ trên cùng 1 mặt phẳng tọa độ đồ thị của các hàm số
y=-2x(1)
y=0,5x(2)
=> chứng minh rằng góc AOB =90o(2 đường thẳng (1)(2) vuông góc vs nhau)
giúp với
Những câu hỏi liên quan
a) Vẽ đồ thị các hàm số sau trên cùng một mặt phẳng tọa độ:y 2x (1); y 0,5x (2); y -x + 6 (3)b) Gọi các giao điểm của đường thẳng có phương trình (3) với hai đường thẳng có phương trình (1) và (2) theo thứ tự là A và B. Tìm tọa độ của hai điểm A và B.c) Tính các góc của tam giác OAB.Hướng dẫn câu c)Tính OA, OB rồi chứng tỏ tam giác OAB là tam giác cân.
T
í
n
h
AOB
^
,
AOx
^...
Đọc tiếp
a) Vẽ đồ thị các hàm số sau trên cùng một mặt phẳng tọa độ:
y = 2x (1); y = 0,5x (2); y = -x + 6 (3)
b) Gọi các giao điểm của đường thẳng có phương trình (3) với hai đường thẳng có phương trình (1) và (2) theo thứ tự là A và B. Tìm tọa độ của hai điểm A và B.
c) Tính các góc của tam giác OAB.
Hướng dẫn câu c)
Tính OA, OB rồi chứng tỏ tam giác OAB là tam giác cân.
T í n h AOB ^ , AOx ^ − BOx ^
a) – Vẽ đồ thị y = 2x (1):
Cho x= 0 ⇒ y= 0 ta được O (0, 0)
Cho x= 2 ⇒ y = 4 ta được điểm (2; 4)
- Vẽ đồ thị y = 0,5x (2):
Cho x= 0 ⇒ y = 0 ta được O (0; 0)
Cho x = 4 ⇒ y = 2 ta được điểm (4; 2)
- Vẽ đồ thị y = -x + 6 (3):
Cho x = 0 ⇒ y = 6 được điểm (0; 6)
Cho y = 0 ⇒ x = 6 được điểm (6; 0)
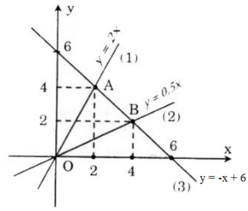
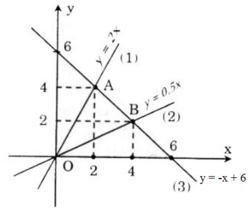
b) Theo đề bài A, B theo thứ tự là giao điểm của đường thẳng (3) với các đường thẳng (1) và (2), nên ta có:
Hoành độ giao điểm của A là nghiệm của phương trình:
- x + 6 = 2x ⇒ x = 2
=> y = 4 => A(2; 4)
Hoành độ giao điểm của B là nghiệm của phương trình:
- x + 6 = 0,5x ⇒ x = 4
⇒ y = 2 ⇒ B(4; 2)
c) Ta có:
Đúng 0
Bình luận (0)
a) Vẽ trên cùng một mặt phẳng tọa độ đồ thị của các hàm số :
y-2x (1)
y0,5x (2)
b) Qua điểm K(0; 2) vẽ đường thẳng (d) song song với trục Ox. Đường thẳng (d) cắt các đường thẳng (1), (2) lần lượt tại A và B. Tìm tọa độ của các điểm A, B
c) Hãy chứng tỏ rằng widehat{AOB}90^0 (hai đường thẳng (1) và (2) vuông góc với nhau)
Đọc tiếp
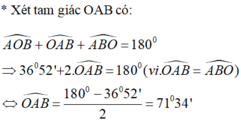
a) Vẽ trên cùng một mặt phẳng tọa độ đồ thị của các hàm số :
\(y=-2x\) (1)
\(y=0,5x\) (2)
b) Qua điểm K(0; 2) vẽ đường thẳng (d) song song với trục Ox. Đường thẳng (d) cắt các đường thẳng (1), (2) lần lượt tại A và B. Tìm tọa độ của các điểm A, B
c) Hãy chứng tỏ rằng \(\widehat{AOB}=90^0\) (hai đường thẳng (1) và (2) vuông góc với nhau)
Từ đó ta có :
\(\widehat{AOK}=\widehat{OBK}\)
Mà \(\widehat{OBK}+\widehat{KOB}=90^0\) nên \(\widehat{AOK}+\widehat{KOB}=90^0\)
Đúng 0
Bình luận (0)
a) Vẽ đồ thị hai hàm số sau trên cùng một mặt phẳng tọa độ:y 0,5x + 2 (1); y 5 – 2x (2)b) Gọi giao điểm của các đường thẳng y 0,5x + 2 và y 5 – 2x với trục hoành theo thứ tự là A, B và gọi giao điểm của hai đường thẳng đó là C.Tìm tọa độ của các điểm A, B, C.c) Tính độ dài các đoạn thẳng AB, AC và BC (đơn vị đo trên các trục tọa độ là xentimet) (làm tròn đến chữ số thập phân thứ hai).d) Tính các góc tạo bởi các đường thẳng có phương trình (1) và (2) với trục Ox (làm tròn đến...
Đọc tiếp
a) Vẽ đồ thị hai hàm số sau trên cùng một mặt phẳng tọa độ:
y = 0,5x + 2 (1); y = 5 – 2x (2)
b) Gọi giao điểm của các đường thẳng y = 0,5x + 2 và y = 5 – 2x với trục hoành theo thứ tự là A, B và gọi giao điểm của hai đường thẳng đó là C.
Tìm tọa độ của các điểm A, B, C.
c) Tính độ dài các đoạn thẳng AB, AC và BC (đơn vị đo trên các trục tọa độ là xentimet) (làm tròn đến chữ số thập phân thứ hai).
d) Tính các góc tạo bởi các đường thẳng có phương trình (1) và (2) với trục Ox (làm tròn đến phút).
a) - Vẽ đồ thị hàm số y = 0,5x + 2 (1)
Cho x = 0 => y = 2 được D(0; 2)
Cho y = 0 => 0 = 0,5.x + 2 => x = -4 được A(-4; 0)
Nối A, D ta được đồ thị của (1).
- Vẽ đồ thị hàm số y = 5 – 2x (2)
Cho x = 0 => y = 5 được E(0; 5)
Cho y = 0 =>0 = 5 – 2x => x = 2,5 được B(2,5; 0)
Nối B, E ta được đồ thị của (2).
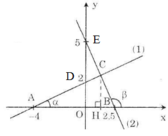
b) Ở câu a) ta tính được tọa độ của hai điểm A và B là A(-4 ; 0) và B (2,5 ; 0)
Hoành độ giao điểm C của hai đồ thị (1) và (2) là nghiệm của phương trình:
0,5 x + 2 = 5 - 2x
⇔ 0,5x + 2x = 5 – 2
⇔ 2,5.x = 3 ⇔ x = 1,2
⇒ y = 0,5.1,2 + 2 = 2, 6
Vậy tọa độ điểm C(1,2; 2,6).
c) AB = AO + OB = |-4| + |2,5| = 6,5 (cm)
Gọi H là hình chiếu của C trên Ox, ta có H( 1,2; 0)
Ta có: AH = AO + OH = 4 + 1,2 = 5,2
BH = BO – OH = 2,5 – 1,2 = 1,3
CH = 2,6
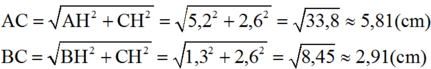
d) Gọi α là góc hợp bởi đường thẳng y = 0,5x + 2 với tia Ox.
Ta có: tgα = 0,5 => α = 26o34'
Gọi β là góc hợp bởi đường thẳng y = 5 - 2x với tia Ox
Tam giác OEB vuông tại O nên:
Đúng 0
Bình luận (0)
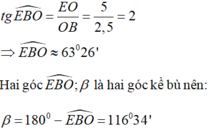
Vẽ trên cùng một mặt phẳng tọa độ đồ thị của các hàm sô:
y = -2x (1)
y = 0,5x (2)
*Vẽ đồ thị hàm số y = -2x
Cho x = 0 thì y = 0. Ta có: O(0; 0)
Cho x = 1 thì y = -2. Ta có: M(1; -2)
Đồ thị hàm số y = -2x đi qua O và M
*Vẽ đồ thị hàm số y = 0,5x
Cho x = 0 thì y = 0. Ta có: O(0; 0)
Cho x = 2 thì y = 1. Ta có: N(2; 1)
Đồ thị hàm số y = 0,5x đi qua O và N.
Đúng 0
Bình luận (0)
a) Tìm hệ số góc của đường thẳng đi qua gốc tọa độ và đi qua điểm A(2; 1)
b) Tìm hệ số góc của đường thẳng đi qua gốc tọa độ và đi qua điểm B( 1; -2)
c) Vẽ đồ thị của các hàm số với hệ số góc tìm được ở các câu a), b) trên cùng một mặt phẳng tọa độ và chứng tỏ rằng hai đường thẳng đó vuông góc với nhau
a. Vẽ trên cùng một mặt phẳng tọa độ đồ thị của các hàm sô:
y = -2x (1)
y = 0,5x (2)
b. Qua điểm K(0; 2) vẽ đường thẳng (d) song song với trục Ox. Đường thẳng (d) cắt các đường thẳng (1) và (2) lần lượt tại A và B. Tìm tọa độ của các điểm A, B.
c. Hãy chứng tỏ rằng góc (AOB) = 90o (hai đường thẳng y = -2x và y = 0,5x vuông góc với nhau).
Cho hàm số y − 2x + 3 có đồ thị là đường thẳng (d1) và hàm số y 0,5x – 2 có đồ thị là đường thẳng (d2). 1. Vẽ đường thẳng (d1) và (d2) cùng trên một mặt phẳng tọa độ2. Tìm tọa độ giao điểm C của hai đường thẳng (d1) và (d2) bằng phép toán3. Gọi A, B thứ tự là giao điểm của đường thẳng (d1) và (d2) với trục Oy. Tính diện tích tam giác ABC (đơn vị đo trên các trục tọa độ là cm)
Đọc tiếp
Cho hàm số y = − 2x + 3 có đồ thị là đường thẳng (d1) và hàm số y = 0,5x – 2 có đồ thị là đường thẳng (d2). 1. Vẽ đường thẳng (d1) và (d2) cùng trên một mặt phẳng tọa độ2. Tìm tọa độ giao điểm C của hai đường thẳng (d1) và (d2) bằng phép toán3. Gọi A, B thứ tự là giao điểm của đường thẳng (d1) và (d2) với trục Oy. Tính diện tích tam giác ABC (đơn vị đo trên các trục tọa độ là cm)
Vẽ đồ thị các hàm số sau trên cùng một mặt phẳng tọa độ:
y = 2x (1); y = 0,5x (2); y = -x + 6 (3)
– Vẽ đồ thị y = 2x (1):
Cho x= 0 ⇒ y= 0 ta được O (0, 0)
Cho x= 2 ⇒ y = 4 ta được điểm (2; 4)
- Vẽ đồ thị y = 0,5x (2):
Cho x= 0 ⇒ y = 0 ta được O (0; 0)
Cho x = 4 ⇒ y = 2 ta được điểm (4; 2)
- Vẽ đồ thị y = -x + 6 (3):
Cho x = 0 ⇒ y = 6 được điểm (0; 6)
Cho y = 0 ⇒ x = 6 được điểm (6; 0)
Đúng 0
Bình luận (0)
Vẽ đồ thị của các hàm số với hệ số góc tìm được ở câu a, b trên cùng một mặt phẳng tọa độ và chứng tỏ rằng hai đường thẳng đó vuông góc với nhau.
Đường thẳng đi qua gốc tọa độ có dạng y = ax + b
Với a = 1/2 ta có hàm sô: y = 1/2.x
Với a = -2 ta có hàm số: y = -2x
*Vẽ đồ thị hàm số y = 1/2.x
Cho x = 0 thì y = 0. Ta có: O(0; 0)
Cho x = 2 thì y = 1. Ta có: A(2; 1)
Đồ thị hàm số y = 1/2.x đi qua O và A
*Vẽ đồ thị hàm số y = -2x
Cho x = 0 thì y = 0. Ta có: O(0; 0)
Cho x = 1 thì y = -2. Ta có: B(1; -2)
Đồ thị hàm số y = -2x đi qua O và B.
*Gọi A’, B’ lần lượt là hình chiếu của A, B trên Ox và Oy.
Ta có hai tam giác AA’O và BB’O có hai cạnh góc vuông tương ứng bằng nhau nên chúng bằng nhau.
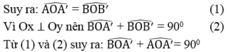
Vậy OA ⊥ OB hay hai đường thẳng y = 1/2.x và y = -2x vuông góc với nhau.
Đúng 0
Bình luận (0)