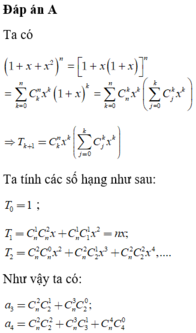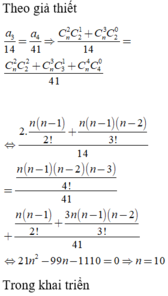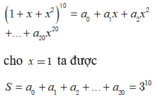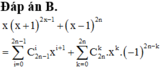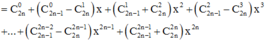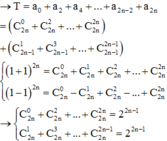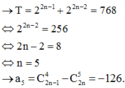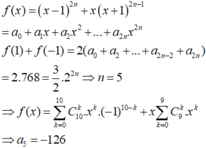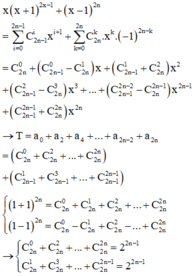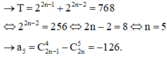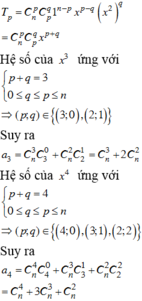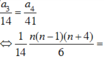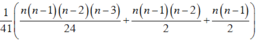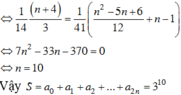cmr a2n+1+b2n+1 bằng (a+b)(a2n-a2n-1.b+a2n-2.b2+...+a2n.b2n-2-a.b2n

Những câu hỏi liên quan
Cho 2n số nguyên dương a1, a2, a3,......, a2n-1, a2n thỏa mãn:a12 + a32 + a52 + ..... + a2n-12 a22 + a42 + a562 + ..... + a2n2 Chứng minh rằng a1 + a2 + a3 + ...... + a2n-1 + a2n là hợp số (n in N*)
Đọc tiếp
Cho 2n số nguyên dương a1, a2, a3,......, a2n-1, a2n thỏa mãn:
a12 + a32 + a52 + ..... + a2n-12 = a22 + a42 + a562 + ..... + a2n2
Chứng minh rằng a1 + a2 + a3 + ...... + a2n-1 + a2n là hợp số (n \(\in\) N*)
cho a,b là hai số tự nhiên. chứng minh (a2n+1 + b2n+1) chia hết cho (a+b) với mọi số tự nhiên n
Với \(n=1\Leftrightarrow a^3+b^3=\left(a+b\right)\left(a^2-ab+b^2\right)⋮\left(a+b\right)\)
Giả sử \(n=k\Leftrightarrow\left(a^{2k+1}+b^{2k+1}\right)⋮\left(a+b\right)\)
Với \(n=k+1\)
Cần cm: \(\left(a^{2k+3}+b^{2k+3}\right)⋮\left(a+b\right)\left(1\right)\)
\(\Leftrightarrow a^{2k+3}+b^{2k+3}=a^{2k+1}\cdot a^2+b^{2k+1}\cdot b^2\\ =a^{2k+1}\cdot a^2+b^{2k+1}\cdot a^2-b^{2k+1}\cdot a^2+b^{2k+1}\cdot b^2\\ =a^2\left(a^{2k+1}+b^{2k+1}\right)-b^{2k+1}\left(a^2-b^2\right)\)
Do \(\left(a^{2k+1}+b^{2k+1}\right)⋮\left(a+b\right);\left(a^2-b^2\right)⋮\left(a-b\right)\)
Do đó \(\left(1\right)\) luôn đúng
Theo pp quy nạp suy ra đpcm
Đúng 2
Bình luận (0)
Cho khai triển
1
+
x
+
x
2
n
a
0
+
a
1
x
+
a
2
x
2
+
....
Đọc tiếp
Cho khai triển 1 + x + x 2 n = a 0 + a 1 x + a 2 x 2 + . . . + a 2 n x 2 n ,
với n ≥ 2 và a 0 , a 1 , a 2 , . . . , a 2 n là các hệ số. Biết rằng a 3 14 = a 4 41 khi đó tổng S = a 0 + a 1 + a 2 + . . . + a 2 n bằng
A. S = 3 10
B. S = 3 11
C. S = 3 12
D. S = 3 13
Cho khai triển
1
+
x
+
x
2
n
a
0
+
a
1
x
+
a
2
x
2
+
...
+
a
2...
Đọc tiếp
Cho khai triển 1 + x + x 2 n = a 0 + a 1 x + a 2 x 2 + ... + a 2 n x 2 n , với n ≥ 2 và a 0 , a 1 , a 2 , ... , a 2 n là các hệ số. Biết rằng a 3 14 = a 4 41 khi đó tổng S = a 0 + a 1 + a 2 + ... + a 2 n bằng
A. S = 3 10 .
B. S = 3 11 .
C. S = 3 12 .
D. S = 3 13 .
Đáp án A
Ta có: 1 + x + x 2 n = 1 + x 1 + x n = ∑ k = 0 n C k n x k 1 + x k
= ∑ k = 0 n C n k x k ∑ j = 0 k C j k x k ⇒ T k + 1 = C k n x k ∑ j = 0 k C j k x k
Ta tính các số hạng như sau:
T 0 = 1 ;
T 1 = C n 1 C n 2 x + C n 1 C 1 1 x 2 = n x ; T 2 = C n 2 C n 0 x 2 + C n 2 C 2 1 x 3 + C n 2 C 2 2 x 4 , ....
Như vậy ta có:
a 3 = C n 2 C 2 1 + C n 3 C 2 0 ; a 4 = C n 2 C 2 2 + C n 3 C 3 1 + C n 4 C 4 0
Theo giả thiết
a 3 14 = a 4 41 ⇒ C n 2 C 2 1 + C n 3 C 2 0 14 = C n 2 C 2 2 + C n 3 C 3 1 + C n 4 C 4 0 41
⇔ 2. n n − 1 2 ! + n n − 1 n − 2 3 ! 14 = n n − 1 2 ! + 3 n n − 1 n − 2 3 ! + n n − 1 n − 2 n − 3 4 ! 41
⇔ 21 n 2 − 99 n − 1110 = 0 ⇒ n = 10
Trong khai triển:
1 + x + x 2 10 = a 0 + a 1 x + a 2 x 2 + ... + a 20 x 20
cho x = 1 ta được: S = a 0 + a 1 + a 2 + ... + a 20 = 3 10
Đúng 0
Bình luận (0)
Cho khai triển
1
+
x
+
x
2
n
a
0
+
a
1
x
+
a
2
x
2
+
.
.
.
+
a
2...
Đọc tiếp
Cho khai triển 1 + x + x 2 n = a 0 + a 1 x + a 2 x 2 + . . . + a 2 n x 2 n ,với n ≥ 2 và a 0 , a 1 , a 2 , . . . , a 2 n là các hệ số. Biết rằng a 3 14 = a 4 41 , khi đó tổng S = a 0 + a 1 + a 2 + . . . + a 2 n bằng
A. S = 3 10
B. S = 3 11
C. S = 3 12
D. S = 3 14
Cho số nguyên
n
≥
3
. Giả sử ta có khai triển
x
-
1
2
n
+
x
x
+
1
2
n
-
1...
Đọc tiếp
Cho số nguyên n ≥ 3 . Giả sử ta có khai triển
x - 1 2 n + x x + 1 2 n - 1 = a 0 + a 1 x + a 2 x 2 + . . . + a 2 n x 2 n . Biết rằng tổng a + a 2 + . . . + a 2 n - 2 + a 2 n = 768 . Tính a 5
A. 294
B. -126
C. 378
D. -84
Cho số nguyên
n
≥
3
. Khai triển:
x
−
1
2
n
+
x
x
+
1
2
n
−
1
a
0
+
a...
Đọc tiếp
Cho số nguyên n ≥ 3 . Khai triển:
x
−
1
2
n
+
x
x
+
1
2
n
−
1
=
a
0
+
a
1
x
+
a
2
x
2
+
...
+
a
2
n
x
2
n
Biết rằng tổng
a
0
+
a
2
+
...
+
a
2
n
−
2
+
a
2
n
=
768
. Tính
a
5
.
A. 294
B. -126
C. 378
D. -84
Cho số nguyên
n
≥
3
. Giả sử ta có khai triển
x
−
1
2
n
+
x
x
+
1
2
n
−
1
a
0
+...
Đọc tiếp
Cho số nguyên n ≥ 3 . Giả sử ta có khai triển
x − 1 2 n + x x + 1 2 n − 1 = a 0 + a 1 x + a 2 x 2 + ... + a 2 n x 2 n . Biết rằng tổng a 0 + a 2 + ... + a 2 n − 2 + a 2 n = 768. Tính a 5 .
A. a 5 = 294.
B. a 5 = − 126.
C. a 5 = 378.
D. a 5 = − 84.
Cho khai triển
1
+
x
+
x
2
a
0
+
a
1
x
+
a
2
x
2
+
.
.
.
+
a
2
n
x...
Đọc tiếp
Cho khai triển 1 + x + x 2 = a 0 + a 1 x + a 2 x 2 + . . . + a 2 n x 2 n với n ≥ 2 và a 0 , a 1 , a 2 , . . . , a 2 n là các hệ số. Tính tổng S = a 0 + a 1 + a 2 + . . . + a 2 n biết a 3 14 = a 4 41
A. S = 3 10
B. S = 3 12
C. S = 2 10
D. S = 2 12
Cho khai triển
1
+
x
+
x
2
n
a
0
+
a
1
x
+
a
2
x
2
+
.
.
.
+
a
2...
Đọc tiếp
Cho khai triển 1 + x + x 2 n = a 0 + a 1 x + a 2 x 2 + . . . + a 2 n x 2 n với n ≥ 2 và a 0 , a 1 , a 2 , . . . , a 2 n là các hệ số. Tính tổng S = a 0 + a 1 + a 2 + . . . + a 2 n biết a 3 14 = a 14 41
A. 3 10
B. 3 12
C. 2 10
D. 2 12