Cho \(\Delta ABC\) có B=C, vẽ tia phân giác góc A cắt BC tại D, gọi Ax là tia phân giác góc ngoài của đỉnh A
CMR AD\(\perp BC\)
Ax//BC
Những câu hỏi liên quan
cho tam giác ABC có B=C kẻ phân giác góc A cắt C tại D gọi Ax là tia phân giác góc ngoài đỉnh A tại điểm A
CMR AD+BC=180
Ax// BC
Cho \(\Delta ABC\) có B=C, phân giác AD (\(D\in BC\)) của A. Gọi à là tia phân giác của góc ngoài tại A.
a) CMR: AD vuông góc với BC
b) CMR: Ax//BC
Cho tam giác ABC có góc B = góc C = 40 độ . Gọi Ax là tia phân giác của góc ngoài ở đỉnh A . Hãy chứng tỏ rằng Ax // BC tren tia doi cua tia bc lay diem d tren tia doi cua tia cb lay diem e sao cho bd=ce cmr: ad=ae
1 ) Cho tam giác ABC có góc B = góc C = 40 độ . Gọi Ax là tia phân giác của góc ngoài tại đỉnh A . Chứng minh rằng : Ax//Bc
2 ) Cho tam giác ABC vuông tại A . Vẽ AH vuông góc với BC . Các tia phân giác của các góc BAH và góc C cắt nhau tại K . Chứng minh rằng : AK vuông góc với CK
Cho tam giác ABC có B=C=40 Gọi Ax là tia phân giác của góc ngoài ở đỉnh A trên tia Ax lấy điểm D sao cho AD=BC số đo góc ABC
Cho tam giác ABC. Gọi Ax là tia phân giác của góc ngoài đỉnh A. Kẻ AH vuông góc với BC (H thuộc BC). CMR:
a. Ax // BC
b. AH là tia phân giác của góc BAC
Cho tam giác ABC có AD là tia phân giác góc A. (D thuộc BC). I là 1 điểm trên cạnh AC. Qua I vẽ đường thẳng song song với AD, cắt cạnh BC tại M, cắt đường thẳng AB tại N
a) CMR: góc ANI = góc AIN
b) Vẽ Ax là tia phân giác góc NAI. CMR: Ax vuông góc MN
Gải giúp mik với mik cần gấp.
Cho tam giác ABC có góc B=C=40 độ. Vẽ Ax là tia phân giác ngoài tại đỉnh A. Ay là tia phân giác trong tại đỉnh A. Đg thẳng bất kì đi qua C cắt Ax tại M . Cắt Ay tại N . Vẽ Ak vông với MN
a, Chứng minh rằng Ax // BC và AM vuông với AN
b, CMR góc MAK = MNA
c, CMR góc NAK = AMK
Giúp mk với
Ta có:
\(\widehat{BAC}=180^o-\widehat{ABC}-\widehat{ACB}=180^o-40^o-40^o=100^o\)
Vì Ax là phân giác ngoài \(\widehat{A}\)
\(\Rightarrow\widehat{CAM}=\frac{180^o-\widehat{BAC}}{2}=\frac{180^o-100^o}{2}=40^o\)
\(\Rightarrow\widehat{CAM}=\widehat{BCA}=40^o\)
\(\Rightarrow\)BC // Ax (so le trong)
Vì Ay là phân giác trong \(\widehat{A}\)
\(\Rightarrow\widehat{NAC}=\frac{100^o}{2}=50^o\)
\(\Rightarrow\widehat{NAC}+\widehat{CAM}=50^o+40^o=90^o\)
\(\Rightarrow AM\perp AN\)
b/ Ta có:
\(\widehat{NAM}=\widehat{AKM}=90^o\)
\(\Rightarrow\widehat{MAK}=180^o-\widehat{AKM}-\widehat{AMK}=90^o-\widehat{AMK}=\widehat{MNA}\)
c/ Tương tự câu b
Đúng 0
Bình luận (0)
10 tháng 11 2021 lúc 21:53
Cho tam giác ABC có góc B = góc C = 40o. Gọi Ax là tia phân giác của góc ngoài đỉnh A. Hãy chứng tó Ax // BC.
Ta có: BAy=B+C (góc ngoài của tam giác)
BAy=400+400=800
Ax là p/g của BAy
⇒ A1=A2=400
Ta có: A2=B=400
Mà hai góc này ở vị trí SLT
⇒ BC//Ax
Đúng 1
Bình luận (0)
Ta có: BAy=B+C (góc ngoài của tam giác)
BAy=400+400=800
Ax là p/g của BAy
⇒ A1=A2=400
Ta có: A2=B=400
Mà hai góc này ở vị trí SLT
⇒ BC//Ax
Đúng 1
Bình luận (0)
Cho tam giác ABC có góc B = góc C = 40o. Gọi Ax là tia phân giác của góc ngoài đỉnh A. Hãy chứng tó Ax // BC.
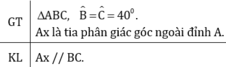
Gọi góc BAy là góc ngoài của tam giác ABC
Mà hai góc này ở vị trí so le trong nên Ax//BC (đpcm).
Đúng 0
Bình luận (0)