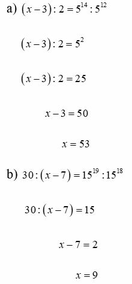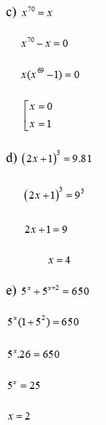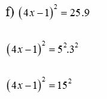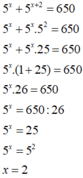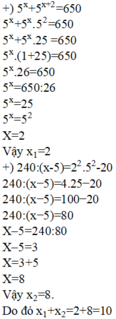a,  x - 3 : 2 = 5 14 : 5 12

=>  x - 3 : 2 = 5 2

=>  x - 3 : 2 = 25

=> x – 3 = 25

=> x = 53

b,  30 : x - 7 = 15 19 : 15 18

=>  30 : x - 7 = 15

=> x – 7 = 2

=> x = 9

c,  x 70 = x

=>  x 70 - x = 0

=>  x ( x 69 - 1 ) = 0

=> 

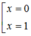
d,  2 x + 1 3 = 9 . 81

=>  2 x + 1 3 = 9 3

=> 2x + 1 = 9

=> x = 4

e,  5 x + 5 x + 2 = 650

=>  5 x 1 + 5 2 = 650

=>  5 x . 26 = 650

=>  5 x = 25

=> x = 2

f,  4 x - 1 2 = 25 . 9

=> 4 x - 1 2 = 5 2 . 3 2

=>  4 x - 1 2 = 15 2

=> 4x – 1 = 15

=> x = 4

Đáp án cần chọn là: B

TK :

5^x + 5^{x +2}     = 650

5^x + 5^x . 5²     = 650

5^x .( 1 +25 )   = 650

5^x .26            = 650

5^x                 = 650 / 26 =25

5^x                = 5²

nên x=2

sao nhieu qua zay

a) \(5^2\cdot3^x=575\)

\(\Rightarrow3^x=\dfrac{575}{5^2}\)

\(\Rightarrow3^x=\dfrac{575}{25}\)

\(\Rightarrow3^x=23\)

Xem lại đề

b) \(5\cdot2^x-7^2=31\)

\(\Rightarrow5\cdot2^x=31+49\)

\(\Rightarrow5\cdot2^x=80\)

\(\Rightarrow2^x=\dfrac{80}{5}\)

\(\Rightarrow2^x=16\)

\(\Rightarrow2^x=2^4\)

\(\Rightarrow x=4\)

c) \(5^x+5^{x+2}=650\)

\(\Rightarrow5^x\cdot\left(1+5^2\right)=650\)

\(\Rightarrow5^x\cdot26=650\)

\(\Rightarrow5^x=\dfrac{650}{26}\)

\(\Rightarrow5^x=25\)

\(\Rightarrow5^x=5^2\)

\(\Rightarrow x=2\)

a, 5² x \(3^x\) = 575 

           3\(^x\) = 575 : 5²

           3\(^x\) = 23

          nếu \(x\) ≤ 0 ta có 3\(^x\) ≤ 1 < 23 (loại) (1)

Nếu \(x\) ≥ 1 ⇒ 3\(^x\) ⋮ 3 \(\ne\) 23 vì 23 không chia hết cho 3 (2)

kết hợp (1) và(2) ta thấy không có giá trị nào của \(x\) thỏa mãn đề bài

Kết luận: \(x\in\varnothing\) 

a23

b4

c2

Đáp án cần chọn là: B

a)\(A=\frac{x^2}{5x+25}+\frac{2x-10}{x}+\frac{50+5x}{x^2+5x}\left(ĐK:x\ne0;-5\right)\)

\(\Leftrightarrow A=\frac{x^2}{5\left(x+5\right)}+\frac{2\left(x-5\right)}{x}+\frac{5\left(x+10\right)}{x\left(x+5\right)}\)

\(\Leftrightarrow A=\frac{x^3+10\left(x^2-25\right)+25x+250}{5x\left(x+5\right)}\)

\(\Leftrightarrow A=\frac{x^3+10x^2+25x}{5x\left(x+5\right)}\)

\(\Leftrightarrow A=\frac{x\left(x+5\right)^2}{5x\left(x+5\right)}\)

\(\Leftrightarrow A=\frac{x+5}{5}\)

b)Để A=-4 \(\Leftrightarrow\frac{x+5}{5}=-4\)

                  \(\Leftrightarrow x+5=-20\)

                   \(\Leftrightarrow x=-25\)

a).....

\(=\frac{x^2}{5\left(x+5\right)}+\frac{2x-10}{x}+\frac{50+5x}{x\left(x+5\right)}\)                                MTC= 5x (x+5)                 ĐK\(\hept{\begin{cases}x\ne0\\x\ne-5\end{cases}}\)

\(=\frac{x^2.x}{5x\left(x+5\right)}+\frac{5.\left(2x-10\right).\left(x+5\right)}{5x\left(x+5\right)}+\frac{5.\left(50+5x\right)}{5x\left(x+5\right)}\)

\(=\frac{x^3+\left(10x-50\right).\left(x+5\right)+250+25x}{5x\left(x+5\right)}\)

\(=\frac{x^3+10x^2+50x-50x-250+250+25x}{5x\left(x+5\right)}\)

\(=\frac{x^3+10x^2+25x}{5x\left(x+5\right)}\)

\(=\frac{x\left(x^2+10x+25\right)}{5x\left(x+5\right)}\)

\(=\frac{x\left(x+5\right)^2}{5x\left(x+5\right)}=\frac{x+5}{5}\)

b) A=-4

=>\(\frac{x+5}{5}=-4\)

=> x = -25

c)

d) Để A đạt gt nguyên thì 5\(⋮\)x+5

=> \(\left(x+5\right)\inƯ\left(5\right)=\left\{1;-1;5;-5\right\}\)

*x+5=1 => x=-4 \(\in Z\)

*x+5=-1 => x=-6\(\in Z\)

*x+5=5  => x=0\(\in Z\)

*x+5=-5  => x=-10\(\in Z\)

Vậy...........

thực hiện phép chia đa thức ta có:

\(x^3-5x^2+9x-2=\left(x^2-2x+3\right)\left(x-3\right)+7\)

=> \(A=x^2-2x+3+\frac{7}{x-3}\)

Với x thuộc Z để A thuộc Z thì \(\frac{7}{x-3}\in Z\)<=> \(7⋮\left(x-3\right)\)<=> x-3 thuộc Ư(7). Em tự làm tiếp nhé!