Giải phương trình:
(x2+3x-4)(x2+x-6)=24
bài 1 giải các bất phương trình sau
a, -x2 +5x-6 ≥ 0
b, x2-12x +36≤0
c, -2x2 +4x-2≤0
d, x2 -2|x-3| +3x ≥ 0
e, x-|x+3| -10 ≤0
bài 2 xét dấu các biểu thức sau
a,<-x2+x-1> <6x2 -5x+1>
b, x2-x-2/ -x2+3x+4
c, x2-5x +2
d, x-< x2-x+6 /-x2 +3x+4 >
Bài 1:
a: \(\Leftrightarrow x^2-5x+6< =0\)
=>(x-2)(x-3)<=0
=>2<=x<=3
b: \(\Leftrightarrow\left(x-6\right)^2< =0\)
=>x=6
c: \(\Leftrightarrow x^2-2x+1>=0\)
\(\Leftrightarrow\left(x-1\right)^2>=0\)
hay \(x\in R\)
giải các phương trình:
a)(x2+3x)(x2+3x+4)=-4
b)x(x+1)(x+2)(x+3)=24
Ta có (\(^{x^{2^{ }}^{ }+3x}\)) (\(^{x^{2^{ }}+3x+4}\))
Đặt \(x^{2^{ }^{ }}+3x\) là a ta có
a.(a+4)=-4
4a+\(a^2\) -4=0
\(^{ }\left(a-2\right)^2\)=0
Suy ra a=2
hay \(x^{2^{ }^{ }^{ }}+3x=2\)
\(x^2+3x-2=0\)
𝑥=−3±17√/2
Giải các phương trình sau:
b) (2x+1)2-2x-1=2
c) (x2-3x)2+5(x2-3x)+6=0
d) (x2-x-1)(x2-x)-2=0
tham khảo
https://hoidapvietjack.com/q/57243/giai-cac-phuong-trinh-sau-a-2x12-2x-12-b-x2-3x-2-5x2-3x60
b) (2x+1)2-2x-1=2
\(< =>4x^2+4x+1-2x-1=2\)
\(< =>4x^2+2x-2=0\)
\(< =>4x^2+4x-2x-2=0\)
\(< =>\left(4x^2+4x\right)-\left(2x+2\right)=0\)
\(< =>4x\left(x+1\right)-2\left(x+1\right)=0\)
\(< =>\left(x+1\right)\left(4x-2\right)=0\)
\(=>\left\{{}\begin{matrix}x+1=0=>x=-1\\4x-2=0=>x=\dfrac{1}{2}\end{matrix}\right.\)
Vậy....
b) (2x+1)2-2x-1=2
<=>4x2+4x+1−2x−1=2
<=>4x2+2x−2=0
<=>4x2+4x−2x−2=0
<=>(4x2+4x)−(2x+2)=0
<=>4x(x+1)−2(x+1)=0
<=>(x+1)(4x−2)=0
1) `x^2+4-2(x-1)=(x-2)^2`
`<=>x^2+4-2x+2=x^2-4x+4`
`<=>-2x+2=-4x`
`<=>2x=-2`
`<=>x=-1`
.
2) ĐKXĐ: `x \ne \pm 3`
`(x+3)/(x-3)-(x-1)/(x+3)=(x^2+4x+6)/(x^2-9)`
`<=>(x+3)^2-(x-1)(x-3)=x^2+4x+6`
`<=>x^2+6x+9-x^2+4x-3=x^2+4x+6`
`<=>10x+6=x^2+4x+6`
`<=>x^2-6x=0`
`<=>x(x-6)=0`
`<=>x=0;x=6`
.
3) ĐKXĐ: `x \ne \pm 3`
`(3x-3)/(x^2-9) -1/(x-3 )= (x+1)/(x+3)`
`<=>(3x-3)-(x+3)=(x+1)(x-3)`
`<=> 2x-6=x^2-2x-3`
`<=>x^2-4x+3=0`
`<=>x^2-x-3x+3=0`
`<=>x(x-1)-3(x-1)=0`
`<=>(x-3)(x-1)=0`
`<=> x=3;x=1`
Vậy...
Giải các phương trình:
a ) 2 x 3 − x 2 + 3 x + 6 = 0 b ) x ( x + 1 ) ( x + 4 ) ( x + 5 ) = 12

b) x.(x+1). ( x+ 4). (x+ 5) = 12
⇔ [ x. (x + 5)]. [(x+1). (x+ 4)] = 12
⇔ x 2 + 5 x ⋅ x 2 + 4 x + x + 4 − 12 = 0 ⇔ x 2 + 5 x ⋅ x 2 + 5 x + 4 − 12 = 0 ( * )
Đặt t = x 2 + 5 x + 2
= > x 2 + 5 x = t – 2 v à x 2 + 5 x + 4 = t + 2
Khi đó phương trình (*) trở thành:
( t – 2). (t+ 2) - 12 = 0
⇔ t 2 − 4 − 12 = 0 ⇔ t 2 − 16 = 0 ⇔ t 2 = 16 ⇔ t = ± 4
+ Với t = 4 ta có: x 2 + 5 x + 2 = 4
⇔ x 2 + 5 x – 2 = 0 ( * * )
Có a= 1, b = 5, c = - 2 và ∆ = 5 2 – 4 . 1 . ( - 2 ) = 33 > 0
Nên (**) có 2 nghiệm phân biệt là:
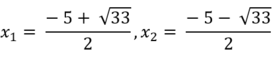
* Với t = - 4 ta có: x 2 + 5 x + 2 = - 4
⇔ x 2 + 5 x + 6 = 0 ( * * * )
Có a= 1, b = 5, c= 6 và ∆ = 5 2 – 4 . 1 . 6 = 1 > 0
Phương trình (***) có 2 nghiệm là:
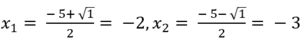
Vậy tập nghiệm của phương trình đã cho là:
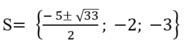
Giải các phương trình:
a ) 2 x 3 − x 2 + 3 x + 6 = 0 b ) x ( x + 1 ) ( x + 4 ) ( x + 5 ) = 12

b) x.(x+1). ( x+ 4). (x+ 5) = 12
⇔ [ x. (x + 5)]. [(x+1). (x+ 4)] = 12
⇔ x 2 + 5 x ⋅ x 2 + 4 x + x + 4 − 12 = 0 ⇔ x 2 + 5 x ⋅ x 2 + 5 x + 4 − 12 = 0 ( * )
Đặt t = x 2 + 5 x + 2
= > x 2 + 5 x = t – 2 v à x 2 + 5 x + 4 = t + 2
Khi đó phương trình (*) trở thành:
( t – 2). (t+ 2) - 12 = 0
⇔ t 2 - 4 - 12 = 0 ⇔ t 2 - 16 = 0 ⇔ t 2 = 16 ⇔ t = ± 4
+ Với t = 4 ta có: x 2 + 5 x + 2 = 4
⇔ x2 +5x – 2 = 0 (**)
Có a= 1, b = 5, c = - 2 và ∆ = 5 2 – 4 . 1 . ( - 2 ) = 33 > 0
Nên (**) có 2 nghiệm phân biệt là:
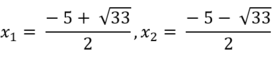
* Với t = - 4 ta có: x 2 + 5 x + 2 = - 4
⇔ x 2 + 5 x + 6 = 0 ( * * * )
Có a= 1, b = 5, c= 6 và ∆ = 5 2 – 4 . 1 . 6 = 1 > 0
Phương trình (***) có 2 nghiệm là:
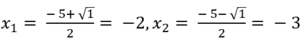
Vậy tập nghiệm của phương trình đã cho là:
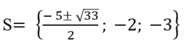
giải bất phương trình sau f(x)=(3x-4)(2x-3)/(x2-5x+6)(5-x)>0
\(f\left(x\right)=\dfrac{\left(3x-4\right)\left(2x-3\right)}{\left(x^2-5x+6\right)\left(5-x\right)}>0\)
\(\Leftrightarrow\dfrac{\left(3x-4\right)\left(2x-3\right)}{\left(x-2\right)\left(x-3\right)\left(5-x\right)}>0\)
Bảng xét dấu:
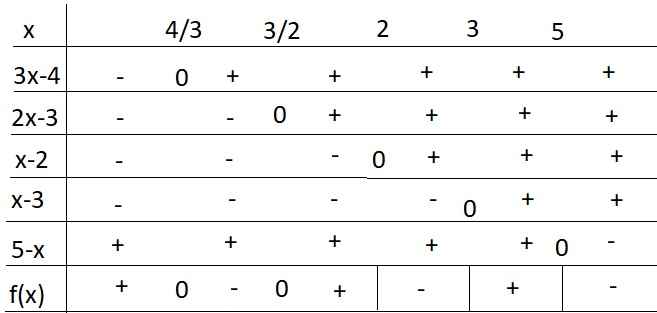
Từ bảng xét dấu ta thấy nghiệm của BPT là: \(\left[{}\begin{matrix}x< 5\\\dfrac{3}{2}< x< 2\\3< x< 5\end{matrix}\right.\)
Hãy giải các phương trình sau đây :
1, x2 - 4x + 4 = 0
2, 2x - y = 5
3, x + 5y = - 3
4, x2 - 2x - 8 = 0
5, 6x2 - 5x - 6 = 0
6,( x2 - 2x )2 - 6 (x2 - 2x ) + 5 = 0
7, x2 - 20x + 96 = 0
8, 2x - y = 3
9, 3x + 2y = 8
10, 2x2 + 5x - 3 = 0
11, 3x - 6 = 0
1) Ta có: \(x^2-4x+4=0\)
\(\Leftrightarrow\left(x-2\right)^2=0\)
\(\Leftrightarrow x-2=0\)
hay x=2
Vậy: S={2}
1.Giải các phương trình sau:
a) 2x2 +16 -6 = 4\(\sqrt{x\left(x+8\right)}\)
b) x4 -8x2 + x-2\(\sqrt{x-1}\) + 16=0
2. Gọi x1;x2 là nghiệm phương trình x2 -3x -7 =0. Không giải phương trình tính các giá trị của biểu thức sau:
A = \(\dfrac{1}{x_1-1}+\dfrac{1}{x_2-1}\)
B= \(x^2_1+x_2^2\)
C= |x1 - x2|
D= \(x_1^4+x_2^4\)
E= (3x1 + x2) (3x2 + x1)
2:
\(A=\dfrac{x_2-1+x_1-1}{x_1x_2-\left(x_1+x_2\right)+1}\)
\(=\dfrac{3-2}{-7-3+1}=\dfrac{1}{-9}=\dfrac{-1}{9}\)
B=(x1+x2)^2-2x1x2
=3^2-2*(-7)
=9+14=23
C=căn (x1+x2)^2-4x1x2
=căn 3^2-4*(-7)=căn 9+28=căn 27
D=(x1^2+x2^2)^2-2(x1x2)^2
=23^2-2*(-7)^2
=23^2-2*49=431
D=9x1x2+3(x1^2+x2^2)+x1x2
=10x1x2+3*23
=69+10*(-7)=-1
Khi giải phương trình 2 - 3 x - 2 x - 3 = 3 x + 2 2 x + 1 , bạn Hà làm như sau:
Theo định nghĩa hai phân thức bằng nhau, ta có:
2 - 3 x - 2 x - 3 = 3 x + 2 2 x + 1
⇔ (2 – 3x)(2x + 1) = (3x + 2)(- 2x – 3)
⇔ -6 x 2 + x + 2 = -6 x 2 – 13x – 6
⇔ 14x = - 8
⇔ x = - 4/7
Vậy phương trình có nghiệm x = - 4/7 .
Em hãy nhận xét về bài làm của bạn Hà.
Đáp số của bài toán đúng nhưng lời giải của bạn Hà chưa đầy đủ.
Lời giải của bạn Hà thiếu bước tìm điều kiện xác định và bước đối chiếu giá trị của x tìm được với điều kiện để kết luận nghiệm.
Trong bài toán trên thì điều kiện xác định của phương trình là:
x ≠ - 3/2 và x ≠ - 1/2
So sánh với điều kiện xác định thì giá trị x = - 4/7 thỏa mãn.
Vậy x = - 4/7 là nghiệm của phương trình.